2. Eine Vorschau

In diesem Kapitel wollen wir anhand zweier konkreter Beispiele eine Vorstellung von einigen Aspekten bekommen, die beim Programmieren eine Rolle spielen. Wir werden diese Aspekte und noch einige mehr in den folgenden Kapiteln genauer besprechen. Es geht hier also nicht darum, schon alles im Detail zu verstehen, sondern vielmehr zunächst einen ersten Eindruck von der computerbasierten Datenanalyse sowie im zweiten Teil von der Struktur eines Programms zu gewinnen.

2.1. Analyse experimenteller Daten

Warnung

Beim Experimentieren mit dem Smartphone ist Vorsicht geboten, um mechanische Beschädigungen auszuschließen. Das Benutzen des Smartphones zu solchen Zwecken geschieht auf eigene Gefahr!

Im ersten Beispiel soll der Zusammenhang zwischen der Winkelgeschwindigkeit \(\omega\) und der Beschleunigung \(a\) bei einer Rotationsbewegung untersucht werden. Gemäß der Mechanik erfährt ein Objekt im Abstand \(r\) von der Drehachse die Beschleunigung

\[a = r\omega^2\,.\]

Zur experimentellen Untersuchung wird ein Smartphone wie in Abb. 2.1 in einer Salatschleuder montiert, und diese in eine Drehung versetzt. Die im Smartphone vorhandenen Sensoren erlauben es, die Winkelgeschwindigkeit und die Beschleunigung mit Hilfe der phyphox-App [1] zu messen.

Abb. 2.1 In einer Salatschleuder montiertes Smartphone mit phyphox-App zur Messung des Zusammenhangs zwischen Rotationsgeschwindigkeit und Beschleunigung (Quelle: Gert-Ludwig Ingold)

Dabei besteht auch die Möglichkeit, die gemessenen Daten herunterzuladen. phyphox packt die Daten sowie einige Metadaten in ein kleines zip-Archiv, das zunächst mit dem Befehl unzip entpackt werden muss. Dabei erhält man unter anderem eine Datei Data.csv, die wir für die weitere Analyse verwenden wollen. Die ersten Zeilen der von der phyphox-Anwendung »Zentripetalbeschleunigung« erzeugten Datei könnten z.B. folgendermaßen aussehen

"Time (s)","Angular velocity (rad/s)","Acceleration (m/s^2)"
5.679032520E-1,2.767693656E-4,3.547039304E-2
1.069169732E0,4.100045423E-4,9.018626044E-3
1.570451470E0,4.192697651E-4,6.790971510E-3
2.071717949E0,3.322073526E-4,4.908061966E-3
2.572999688E0,2.126946028E-3,5.461507249E-3

In der ersten Zeile wird die Bedeutung der drei Spalten angegeben und anschließend folgen für jede Messung drei durch ein Komma getrennte Einträge, die jeweils den Zeitpunkt der Messung, die Winkelgeschwindigkeit und die Beschleunigung umfassen. Die Trennung der Spalten durch Kommas erklärt die Endung csv für comma separated values [2] der Datei. CSV-Dateien lassen sich mit gängigen Tabellenkalkulationsprogrammen wie LibreOffice oder Microsoft Excel öffnen und bearbeiten.

Wir wollen nun durch einzelne Schritte der Datenanalyse gehen, die man gut in einem Jupyter-Notebook durchführen kann. Da wir auf frei verfügbare Programmpakete zurückgreifen wollen, um Daten graphisch darzustellen und die Daten an eine Funktion zu fitten, importieren wir zunächst Namensräume von drei Bibliotheken.

import numpy as np
from scipy import optimize
import matplotlib.pyplot as plt

In einem nächsten Schritt werden die Daten aus der Datei eingelesen und die einzelnen Spalten entsprechenden Variablen zugeordnet.

with open("Data.csv") as csvfile:
    data = np.loadtxt(csvfile, skiprows=1, delimiter=',')
    
time = data[:, 0]
angular_velocity = data[:, 1]
acceleration = data[:, 2]

Beim Einlesen der Daten mit loadtxt aus der NumPy-Bibliothek sorgen wir durch Angabe von skiprows dafür, dass die erste Zeile nicht als Datenzeile behandelt wird. Zudem legen wir mit Hilfe des Arguments delimiter das Komma als Trennzeichen fest.

Damit sind wir schon in der Lage, uns einen graphischen Überblick über die Daten zu verschaffen, indem wir beispielsweise die gemessene Winkelgeschwindigkeit über der Zeit auftragen. Damit die Bedeutung der Achsen klar wird, sehen wir auch eine entsprechende Beschriftung vor.

plt.xlabel("$t$")
plt.ylabel("$\omega$")
plt.plot(time, angular_velocity)

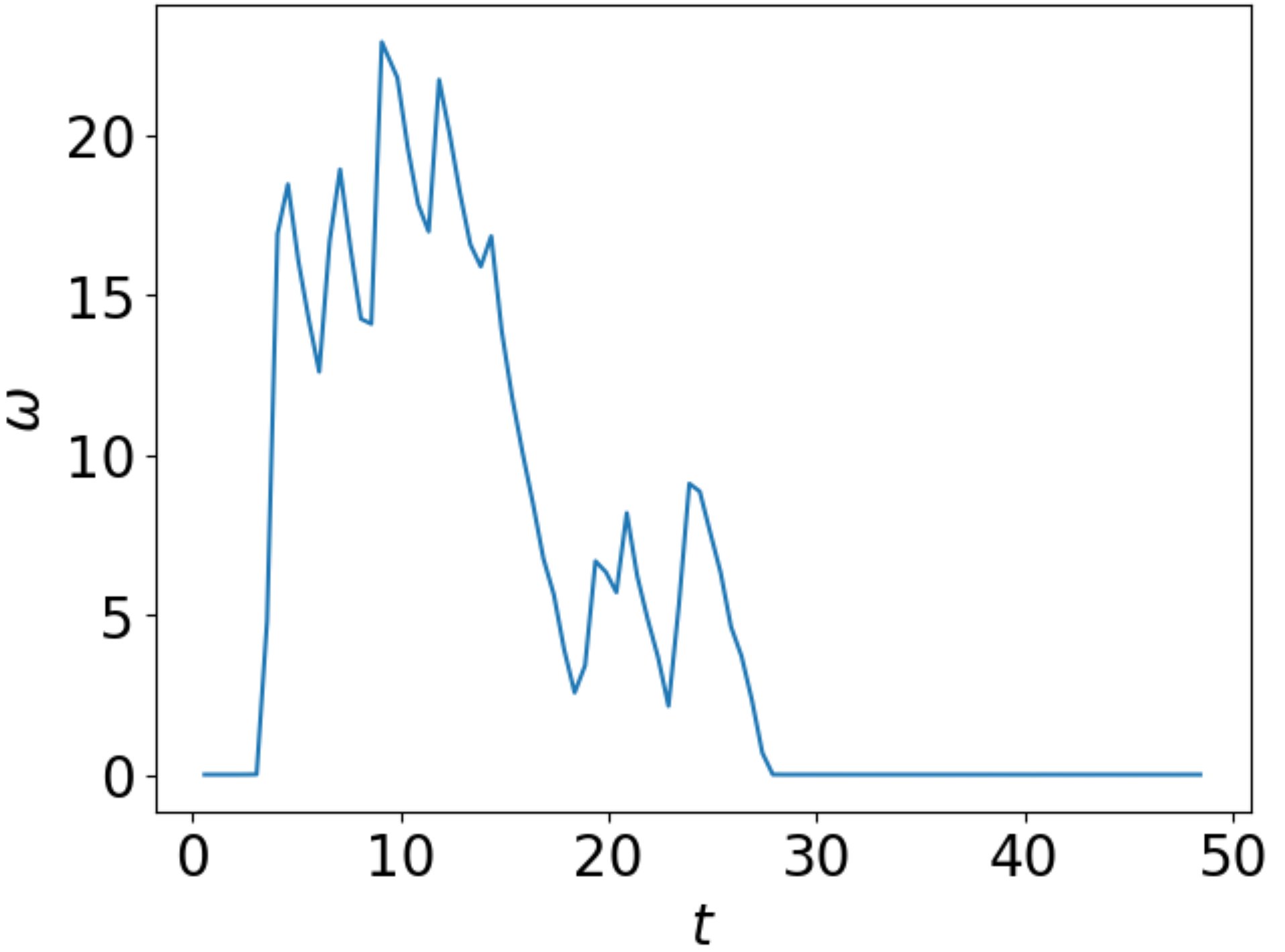
Abb. 2.2 Winkelgeschwindigkeit als Funktion der Zeit

Um den eingangs erwähnten Zusammenhang zwischen Winkelgeschwindigkeit und Beschleunigung analysieren zu können, ist es aber sinnvoller, diese beiden Größen gegeneinander aufzutragen.

plt.xlabel("$\omega$")
plt.ylabel("$a$")
plt.plot(angular_velocity, acceleration, ".")

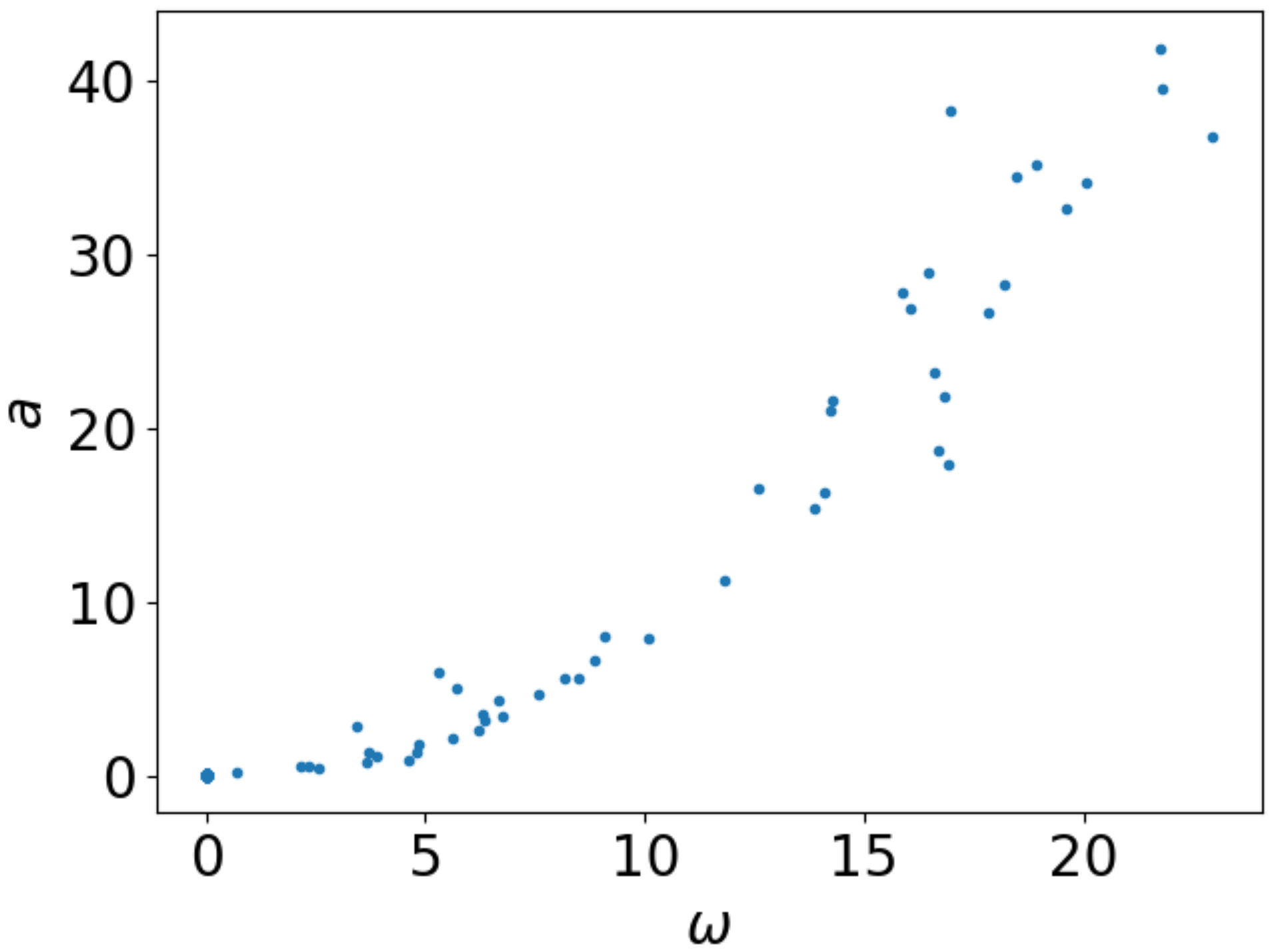
Abb. 2.3 Beschleunigung als Funktion der Winkelgeschwindigkeit

Da die Daten nicht mit zunehmender Winkelgeschwindigkeit vorliegen, haben wir hier zur Darstellung Punkte verwendet und dazu das Argument "." verwendet. Mehr Information zu den vielfältigen Darstellungsmöglichkeiten finden Sie auf der Webseite von matplotlib.

Im nächsten Schritt möchten wir die Daten, die offensichtlich eine nicht unerhebliche Messunsicherheit aufweisen, an eine quadratische Funktion fitten. Dazu definieren wir zunächst eine quadratische Funktion, die den Abstand zwischen Drehachse und Sensor als freien Parameter enthält, und übergeben diese Funktion sowie unsere Daten an die Funktion optimize.curve_fit. Diese Funktion aus dem SciPy-Paket dient dazu, Fits an im Allgemeinen nichtlineare Funktionen vorzunehmen.

def fit_func(x, radius):
    return radius*x**2

popt, pcov = optimize.curve_fit(fit_func, angular_velocity, acceleration)

Uns interessiert vor allem das Ergebnis popt. Dieses Tupel enthält für jeden freien Parameter den gefundenen Optimalwert. In unserem Fall ist dies lediglich der Wert popt[0], der den Abstand zwischen Sensor und Drehachse angibt.

Um die Qualität des Fits optisch beurteilen zu können, ist es sinnvoll, die gefundene Funktion graphisch mit den Daten zusammen aufzutragen.

plt.xlabel("$\omega$")
plt.ylabel("$a$")
plt.plot(angular_velocity, acceleration, ".")
xvalues = np.linspace(0, 20)
yvalues = fit_func(xvalues, popt[0])
plt.plot(xvalues, yvalues)

Dazu wird in den drei letzten Zeilen zunächst ein Vektor mit \(x\)-Werten und anschließend unter Verwendung der Fitfunktion die zugehörigen \(y\)-Werte erzeugt, die abschließend graphisch gemeinsam mit den Messdaten dargestellt werden.

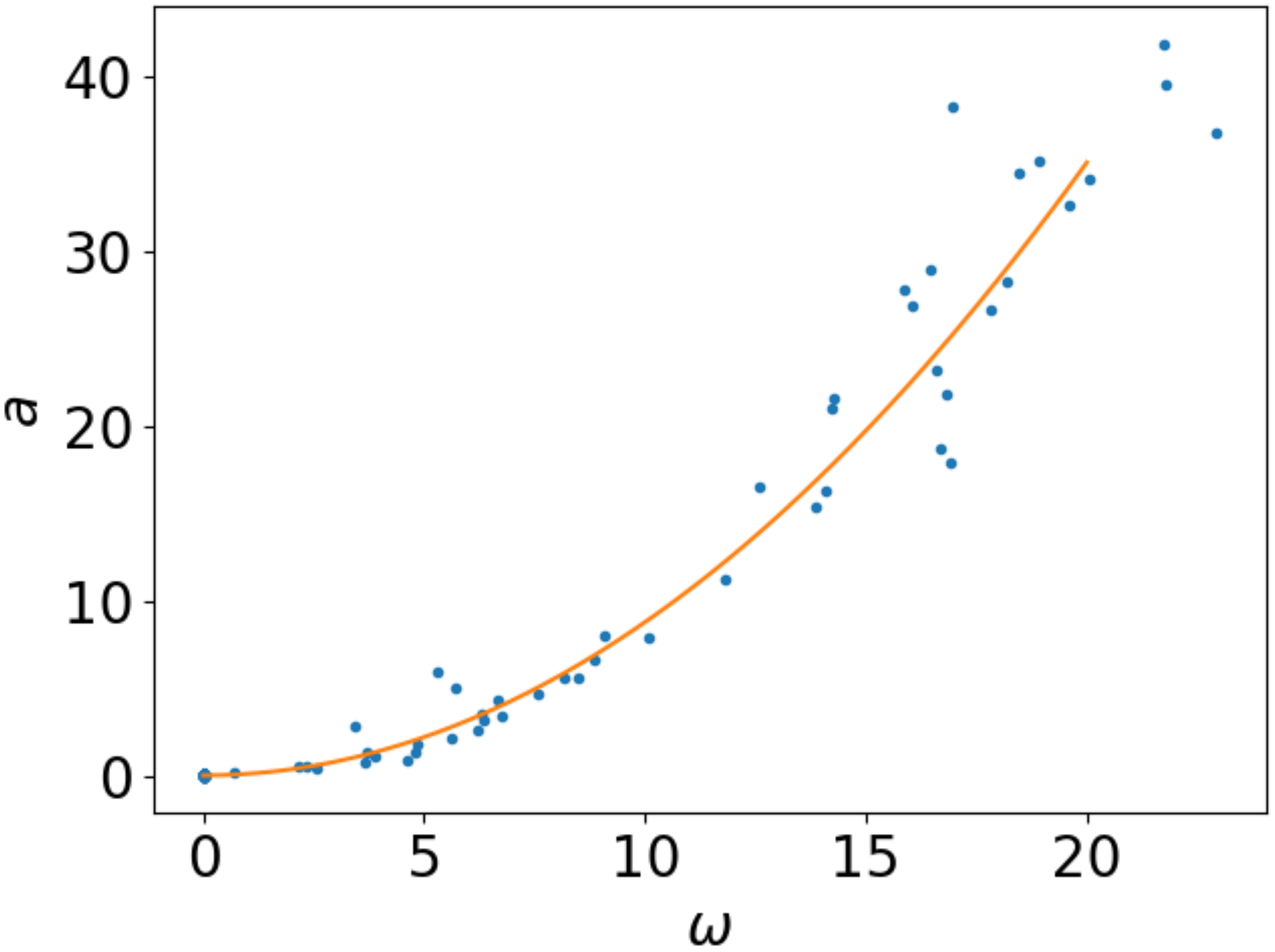
Abb. 2.4 Beschleunigung als Funktion der Winkelgeschwindigkeit: Messdaten in blau und zugehörige Fitfunktion in orange

Zur Analyse von Potenzgesetzen ist häufig eine doppelt-logarithmische Auftragung sinnvoll, da sich der Zusammenhang

\[y = Ax^a\]

durch Logarithmieren auf einen linearen Zusammenhang

\[\log_{10}(y) = a\log_{10}(x) + \log_{10}(A)\]

zwischen dem Logarithmus von \(x\) und dem Logarithmus von \(y\) abbilden lässt. Dabei ist es im Prinzip unerheblich, ob man wie hier den dekadischen Logarithmus oder aber den natürlichen Logarithmus verwendet. Daher tragen wir unsere Messdaten jetzt doppelt-logarithmisch auf.

plt.xscale('log')
plt.yscale('log')
plt.xlabel("$\omega$")
plt.ylabel("$a$")
plt.plot(angular_velocity, acceleration, '.')

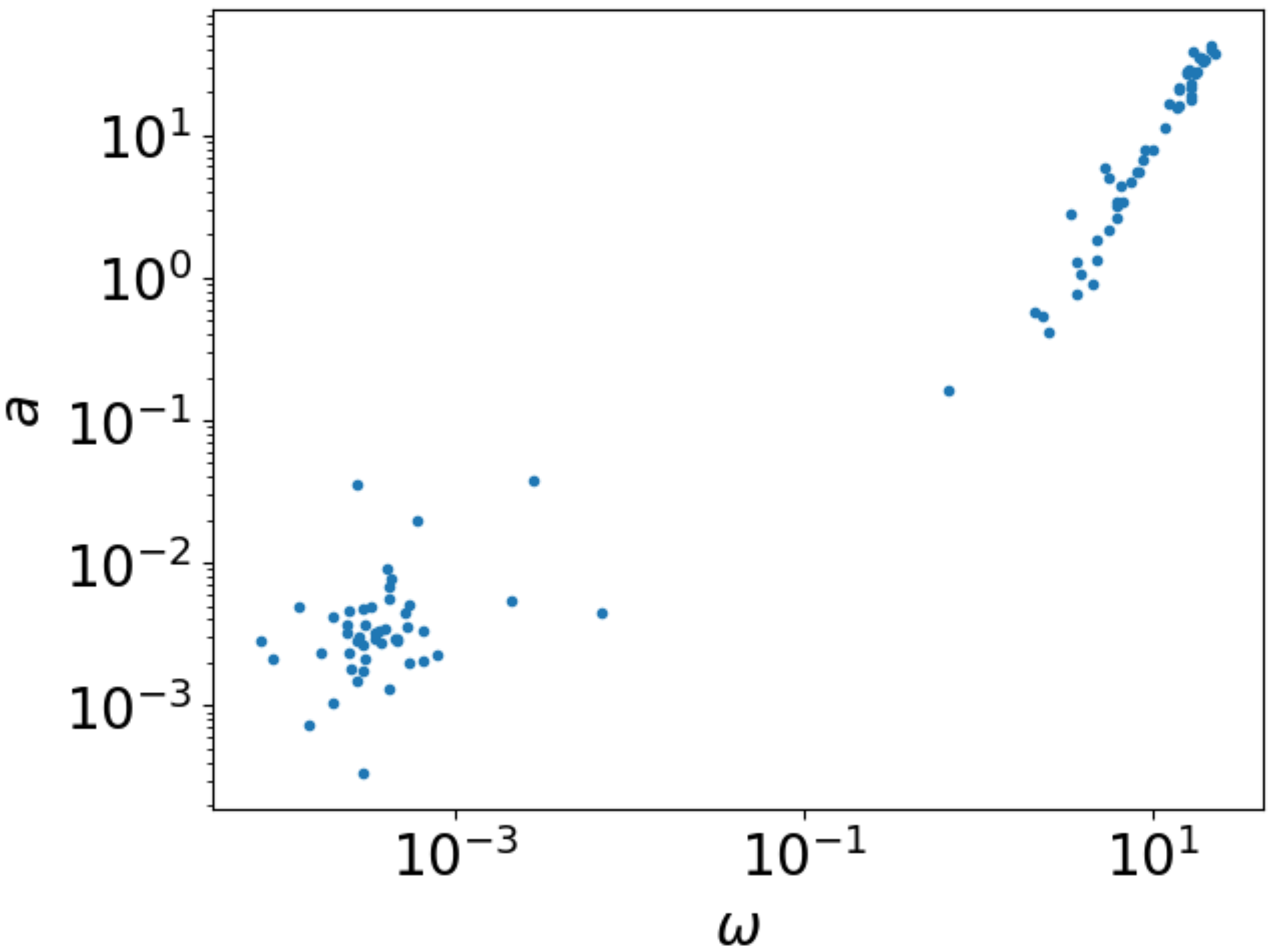
Abb. 2.5 Beschleunigung als Funktion der Winkelgeschwindigkeit in doppelt-logarithmischer Auftragung

Hierbei fällt auf, dass es zwei Datenbereiche gibt. Bei größeren Winkelgeschwindigkeiten ergibt sich ein linearer Zusammenhang, während bei kleinen Winkelgeschwindigkeiten ein Punktehaufen zu sehen ist. Hier befindet sich die Salatschleuder offenbar nicht mehr in einer guten Rotationsbewegung, so dass wir nur Datenpunkte mit einer Winkelgeschwindigkeit größer als 1 1/s berücksichtigen wollen. Dazu definieren wir uns zunächst eine Variable validdata, die die betreffenden Messpunkte identifiziert. Mit ihrer Hilfe können wir die Messdaten auf die gewünschten Daten reduzieren. Zur Kontrolle stellen wir die so erhaltene Untermenge an Daten gleich noch einmal graphisch dar.

validdata = angular_velocity > 1
angular_velocity_1 = angular_velocity[validdata]
acceleration_1 = acceleration[validdata]
plt.xscale('log')
plt.yscale('log')
plt.xlabel("$\omega$")
plt.ylabel("$a$")
plt.plot(angular_velocity_1, acceleration_1, '.')

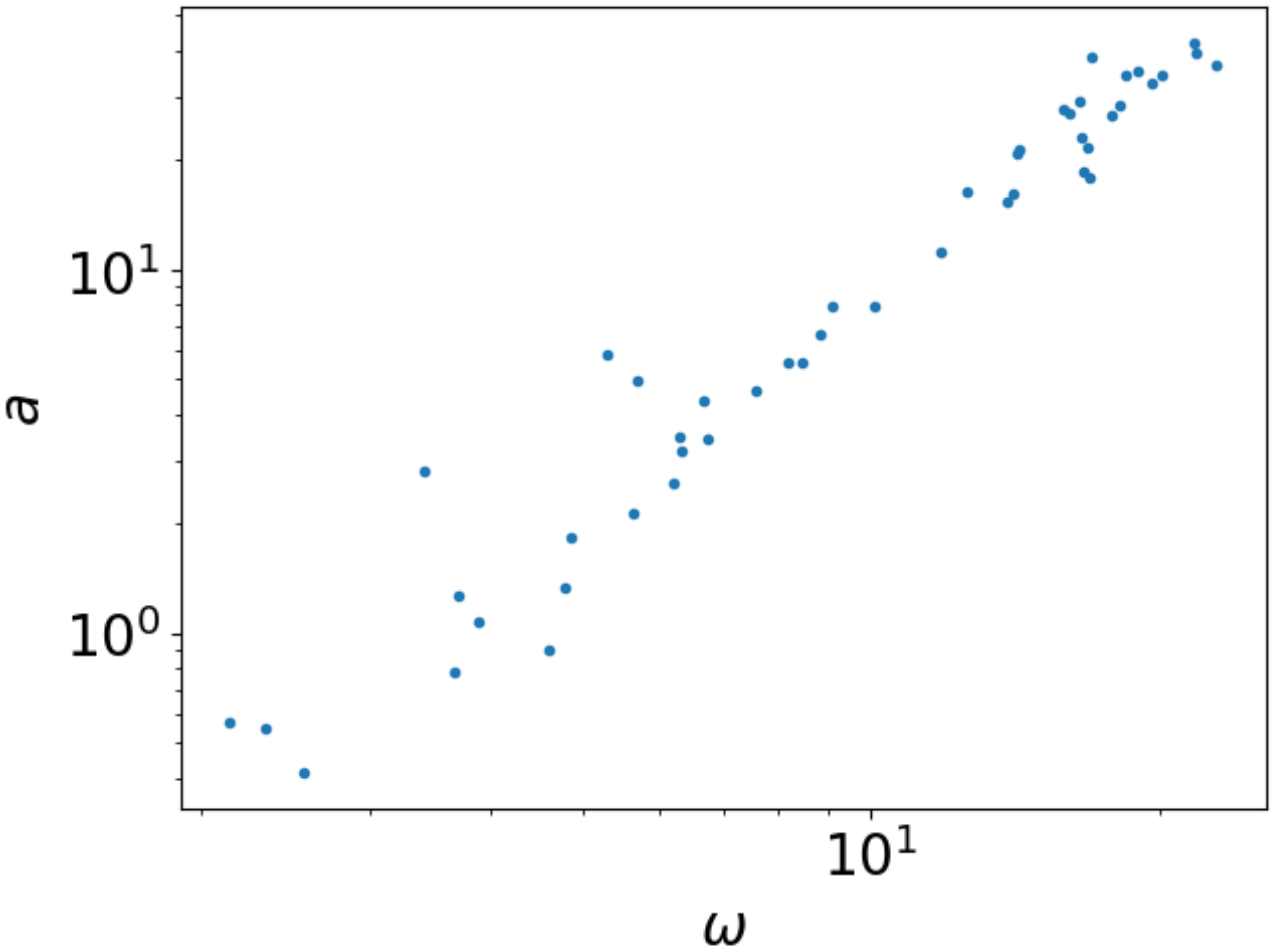
Abb. 2.6 Auswahl der Messdaten für Winkelgeschwindigkeiten größer 1 1/s in doppelt-logarithmischer Auftragung

In Abb. 2.6 haben wir unsere Messdaten doppelt-logarithmisch aufgetragen. Um einen linearen Fit durchführen zu können, müssen wir jedoch den Logarithmus unserer Messdaten bilden. Dann können wir die Daten auch auf einer linearen Skala darstellen und erhalten ein Bild, das äquivalent zur doppelt-logarithmischen Auftragung ist.

log_angular_velocity = np.log10(angular_velocity_1)
log_acceleration = np.log10(acceleration_1)
plt.xlabel("$\log_{10}(\omega)$")
plt.ylabel("$\log_{10}(a)$")
plt.plot(log_angular_velocity, log_acceleration, '.')

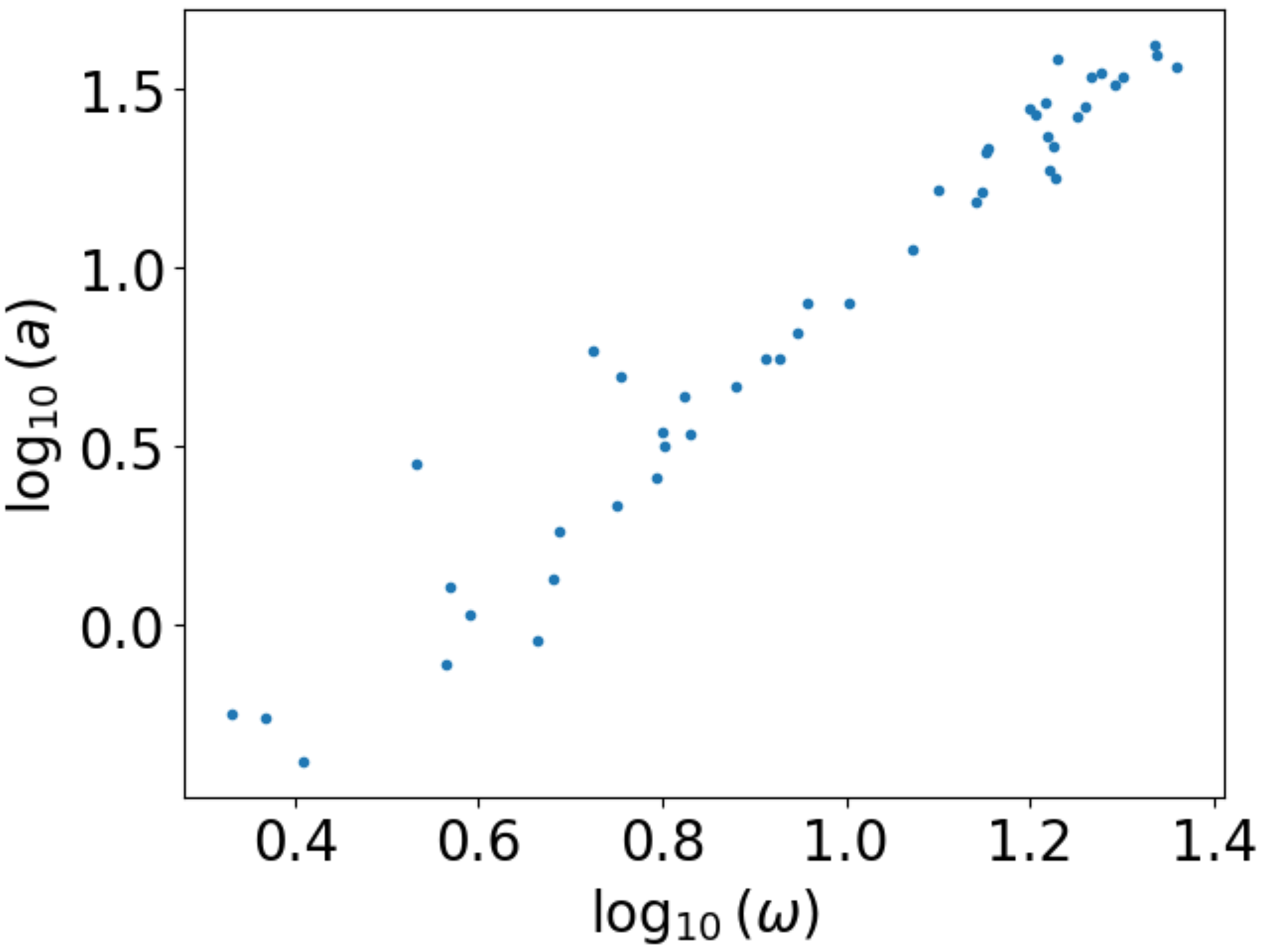
Abb. 2.7 Logarithmierte Messdaten für Winkelgeschwindigkeiten größer 1 1/s in linearer Auftragung

Auch wenn die Auftragung der Daten in Abb. 2.6 und Abb. 2.7 gleich aussieht, erkennt man doch einen Unterschied an den Achsen. In Abb. 2.6 ist die Achseneinteilung nichtlinear, da wir die Originaldaten auf einer logarithmischen Skala auftragen. In Abb. 2.7 sind die Achsen dagegen linear eingeteilt. Dafür sind nun die Logarithmen der Messwerte aufgetragen.

Die logarithmierten Daten können wir nun an eine lineare Funktion fitten.

def lin_fit_func(x, a, b):
    return a*x+b

popt, pcov = optimize.curve_fit(lin_fit_func, log_angular_velocity, log_acceleration)

Dabei ist zu beachten, dass die Fitfunktion im Gegensatz zu der ursprünglich verwendeten quadratischen Funktion zwei Fitparameter besitzt. Die Steigung \(a\) der Kurve gibt dabei den Exponenten an, während der Achsenabschnitt \(b\) dem Logarithmus des Vorfaktors entspricht. In unserem Fall wäre dieser Vorfaktor der Abstand zwischen Sensor und Drehachse.

Der Exponent lässt sich aus popt[0] entnehmen. Für unsere Messdaten ergibt er sich zu etwa 1,987, was in Anbetracht der Messfehler gut zum erwarteten Exponenten 2 passt. Auf eine Analyse der Messfehler wollen wir an dieser Stelle verzichten. Der Abstand zwischen Sensor und Drehachse ergibt sich aus 10**popt[1] zu etwa 9 cm, was gut zu den Dimensionen der Salatschleuder passt. Abschließend stellen wir nochmals unsere Messdaten zusammen mit dem linearen Fit dar, um uns auch auf diese Weise davon zu überzeugen, wie gut die Fitfunktion die Messdaten beschreibt.

plt.xlabel("$\log_{10}(\omega)$")
plt.ylabel("$\log_{10}(a)$")
plt.plot(log_angular_velocity, log_acceleration, '.')
xvalues = np.linspace(0.4, 1.4)
plt.plot(xvalues, popt[0]*xvalues+popt[1])

Abb. 2.8 Logarithmierte Messdaten für Winkelgeschwindigkeiten größer 1 1/s in linearer Auftragung zusammen mit einem linearen Fit

Damit haben wir an einem Beispiel vorgeführt, wie eine einfache Datenanalyse mit Hilfe von Python unter Verwendung einiger wissenschaftlicher Programmbibliotheken vorgenommen werden kann. Die hier zusammengestellte Information, also Code, Abbildungen und Beschreibung würde man in der Praxis in einem einzigen Jupyter-Notebook zusammenfassen und damit die Strategie der Datenanalyse sowie die Ergebnisse in einer Datei dokumentieren.

2.2. Ein erstes Python-Skript

Unser zweites Beispiel implementiert das Spiel »Schere, Stein, Papier«, wobei der Benutzer gegen den Computer spielt. Bei der folgenden Realisierung spielen psychologische Aspekte des Spiels keine Rolle. Bevor wir das Programm ausführen und dann anschließend einen genaueren Blick auf den Code werfen, wollen wir kurz an die Spielregeln erinnern. Spieler und Computer wählen eines der drei Objekte Schere, Stein oder Papier. Die Schere schneidet das Papier, das Papier wickelt den Stein ein und der Stein macht die Schere stumpf. Daher gewinnt die Schere gegen dem Papier, das Papier gegen den Stein und der Stein wiederum gegen die Schere.

Tipp

Durch Klicken auf das Blattsymbol rechts oben im Codefeld kann man leicht den gesamten Code in eine Datei kopieren.

import random

def get_result(n_self, n_other):
    result = (n_self - n_other) % 3
    if result == 0:
        return 'Das Spiel endete unentschieden.'
    elif result == 1:
        return 'Du hast gewonnen.'
    return 'Du hast leider verloren.'

objekte = ['Stein', 'Papier', 'Schere']
info_text = ('\n[0] Stein\n'
             '[1] Papier\n'
             '[2] Schere\n\n'
             'Gib eine Zahl zwischen 0 und 2 ein oder -1 zum Beenden: ')

while True:
    n_benutzer = int(input(info_text))
    if 0 <= n_benutzer <= 2:
        n_computer = random.randrange(3)
        print('-'*40)
        print(f'Benutzer: {objekte[n_benutzer]}')
        print(f'Computer: {objekte[n_computer]}')
        print(get_result(n_benutzer, n_computer))
        print('-'*40)
    elif n_benutzer == -1:
        break
    else:
        print('\n*** ungültige Eingabe\n')

Bevor wir uns mit dem Programmcode beschäftigen, sehen wir uns zunächst eine Beispiellauf an. Das Programm sei in einer Datei schere_stein_papier.py abgespeichert, die jetzt unter der Kontrolle des Python-Interpreters ausgeführt wird. Nach einem Informationstext kann der Benutzer durch Eingabe einer Zahl zwischen 0 und 2 ein Objekt auswählen. Anschließend wählt der Computer ein Objekt und gibt das Spielergebnis aus. Danach sind weitere Spielrunden möglich bis der Benutzer die Zahl -1 eingibt.

$ python schere_stein_papier.py

[0] Stein
[1] Papier
[2] Schere

Gib eine Zahl zwischen 0 und 2 ein oder -1 zum Beenden: 2
----------------------------------------
Benutzer: Schere
Computer: Papier
Du hast gewonnen.
----------------------------------------

[0] Stein
[1] Papier
[2] Schere

Gib eine Zahl zwischen 0 und 2 ein oder -1 zum Beenden: 2
----------------------------------------
Benutzer: Schere
Computer: Schere
Das Spiel endete unentschieden.
----------------------------------------

[0] Stein
[1] Papier
[2] Schere

Gib eine Zahl zwischen 0 und 2 ein oder -1 zum Beenden: -1
$

Schon ohne den Programmcode genau anzusehen, macht die Ausführung des Programms deutlich, dass es möglich sein sollte, Daten einzugeben und die Resultate wieder auszugeben. Vor allem ohne Letzteres wird man kaum auskommen, da das Programm in irgendeiner Form eine Auswirkung haben sollte. Allerdings wird die Eingabe häufig nicht über die Tastatur und die Ausgabe über den Bildschirm erfolgen. Gerade umfangreichere Eingaben erfolgen durch das Einlesen einer oder auch mehrerer Dateien, die beispielsweise experimentelle Daten enthalten. Auch die Ausgabe wird häufig in Dateien erfolgen, zum Beispiel um die Daten für weitere Schritte wie eine graphische Aufbereitung zur Verfügung zu haben.

Sehen wir uns an, wo in unserem Beispielprogramm die Ein- und Ausgabe erfolgt. Die relevanten Zeilen sind farblich hervorgehoben.

import random

def get_result(n_self, n_other):
    result = (n_self - n_other) % 3
    if result == 0:
        return 'Das Spiel endete unentschieden.'
    elif result == 1:
        return 'Du hast gewonnen.'
    return 'Du hast leider verloren.'

objekte = ['Stein', 'Papier', 'Schere']
info_text = ('\n[0] Stein\n'
             '[1] Papier\n'
             '[2] Schere\n\n'
             'Gib eine Zahl zwischen 0 und 2 ein oder -1 zum Beenden: ')

while True:
    n_benutzer = int(input(info_text))
    if 0 <= n_benutzer <= 2:
        n_computer = random.randrange(3)
        print('-'*40)
        print(f'Benutzer: {objekte[n_benutzer]}')
        print(f'Computer: {objekte[n_computer]}')
        print(get_result(n_benutzer, n_computer))
        print('-'*40)
    elif n_benutzer == -1:
        break
    else:
        print('\n*** ungültige Eingabe\n')

Die input()-Funktion erlaubt das Einlesen von Information von der Tastatur. Hinter dem Befehl steht hier in Klammern ein Argument, wie wir das von mathematischen Funktion kennen. Dieses Argument, das hier info_text genannt wurde, enthält den Text, der als Eingabeaufforderung ausgegeben wird. Nach einer Umwandlung der Texteingabe in eine ganze Zahl wird die Eingabe hier der Variablen n_benutzer zugewiesen.

In den Zeilen 21 bis 25 und 29 sehen wir Aufrufe der print()-Funktion, die für die Ausgabe von Information verantwortlich sind. Wie man die genaue Formatierung der Ausgabe steuern kann, werden wir in einem späteren Kapitel sehen.

Weiter fällt bei der Ausführung des Programms auf, dass sich das Spiel wiederholen lässt, im Prinzip beliebig oft bis der Benutzer -1 eingibt. Die Ausführung von so genannten Schleifen ist in Programmen sehr häufig anzutreffen. Dabei kann die Zahl der Schleifendurchläufe vorgegeben sein, wie es in Python bei einer for-Schleife der Fall ist oder von einer Bedingung abhängen, wie in Python durch eine while-Schleife realisiert.

In unserem Programm ist ab der Zeile 17 eine while-Schleife implementiert, die eine etwas ungewöhnliche Form annimmt. Nach dem while-Befehl steht immer eine Bedingung, die je nachdem ob sie erfüllt ist oder nicht, über die Fortsetzung der Schleifendurchläufe entscheidet. Hier sorgt der Wahrheitswert True immer dafür, dass die Bedingung erfüllt ist. Die Schleife wird also im Prinzip unendlich oft durchlaufen. Allerdings haben wir in den Zeilen 26 und 27 eine Vorkehrung getroffen, dass die Schleifendurchläufe bei einer Eingabe von -1 abgebrochen wird.

while True:
    n_benutzer = int(input(info_text))
    if 0 <= n_benutzer <= 2:
        n_computer = random.randrange(3)
        print('-'*40)
        print(f'Benutzer: {objekte[n_benutzer]}')
        print(f'Computer: {objekte[n_computer]}')
        print(get_result(n_benutzer, n_computer))
        print('-'*40)
    elif n_benutzer == -1:
        break
    else:
        print('\n*** ungültige Eingabe\n')

Soeben sind wir einem weiteren typischen Programmierkonstrukt begegnet, nämlich einer Verzweigung. Auch hier passiert wieder etwas in Abhängigkeit davon, ob eine Bedingung erfüllt ist. Allerdings geht es nicht um die Wiederholung eines bestimmten Codes, sondern darum, welcher Code ausgeführt wird. Um die Struktur dieser Konstruktion zu verstehen, sehen wir uns die im Folgenden markierten Zeilen genauer an.

while True:
    n_benutzer = int(input(info_text))
    if 0 <= n_benutzer <= 2:
        n_computer = random.randrange(3)
        print('-'*40)
        print(f'Benutzer: {objekte[n_benutzer]}')
        print(f'Computer: {objekte[n_computer]}')
        print(get_result(n_benutzer, n_computer))
        print('-'*40)
    elif n_benutzer == -1:
        break
    else:
        print('\n*** ungültige Eingabe\n')

In Zeile 19 wird überprüft, ob die Eingabe durch den Benutzer im vorgegebenen Intervall, also zwischen 0 und 2 liegt. In diesem Fall wird eine Spielrunde durchgeführt, die durch die Einrückung verdeutlicht ist. Während andere Programmiersprachen zur Begrenzung eines solchen Blocks häufig Klammern verwenden, erwartet Python eine Einrückung.

Liegt die Eingabe nicht im Intervall zwischen 0 und 2, so müssen wir noch den Fall der Eingabe -1 überprüfen. elif in Zeile 26 steht als Abkürzung für else if. Falls also die Eingabe nicht zwischen 0 und 2 liegt, aber gleich -1 ist, so wird die while-Schleife in Zeile 27 abgebrochen.

Ist keiner der beiden vorgehenden Fälle erfüllt, wird der else-Block ab Zeile 28 relevant, der in unserem in einer Ausgabe darauf hinweist, dass keine gültige Eingabe gemacht wurde.

Eine entsprechende Verzweigungsstrukturen findet man auch in den Zeilen 4 bis 9, wo auch drei Alternativen zu unterscheiden sind, nämlich gewonnen, unentschieden und verloren. Es kann aber auch vorkommen, dass ein if-Block alleine vorkommt oder nur in Kombination mit einem else-Block. Mehr hierzu werden wir später noch erfahren.

Werfen wir ein genaueren Blick auf den ersten Teil des Programmcodes.

import random

def get_result(n_self, n_other):
    result = (n_self - n_other) % 3
    if result == 0:
        return 'Das Spiel endete unentschieden.'
    elif result == 1:
        return 'Du hast gewonnen.'
    return 'Du hast leider verloren.'

objekte = ['Stein', 'Papier', 'Schere']
info_text = ('\n[0] Stein\n'
             '[1] Papier\n'
             '[2] Schere\n\n'
             'Gib eine Zahl zwischen 0 und 2 ein oder -1 zum Beenden: ')

while True:
    n_benutzer = int(input(info_text))
    if 0 <= n_benutzer <= 2:
        n_computer = random.randrange(3)
        print('-'*40)
        print(f'Benutzer: {objekte[n_benutzer]}')
        print(f'Computer: {objekte[n_computer]}')
        print(get_result(n_benutzer, n_computer))
        print('-'*40)
    elif n_benutzer == -1:
        break
    else:
        print('\n*** ungültige Eingabe\n')

In den Zeilen 3 bis 9 ist eine Funktion definiert, die in Abhängigkeit der von Benutzer und Computer gewählten Objekte entscheidet, wer das Spiel gewonnen hat. Diese Funktion wird in Zeile 24 aufgerufen und dorthin wird mit Hilfe einer der return-Anweisungen in den Zeilen 6, 8 und 10 auch das Ergebnis der Funktion zurückgegeben. Im Prinzip könnte der Code im Funktionsblock auch direkt weiter unten im Programm stehen. Hier wird vor durch die Definition einer Funktion vor allem mehr Übersichtlichkeit erreicht.

Häufig kann man auch auf Funktionen zurückgreifen, die von einem anderen Programmpaket bereitgestellt wird. In Python kann dies die sehr umfangreiche Standardbibliothek sein oder ein anderes der unzähligen verfügbaren Programmpakete. In unserem Beispiel haben wir zur Bestimmung der zufälligen Wahl des Objekts durch den Computer auf die Python-Standardbibliothek zurückgegriffen. Dies ist sinnvoll, da die Berechnung guter Zufallszahlen nicht ganz einfach ist. Daher ist es besser, auf bewährten und gut geschriebenen Code zurückgreifen statt das Rad neu zu erfinden. In der Zeile 20 benutzen wir die randrange()-Funktion, um eines der drei Objekte zufällig auszuwählen. Dies ist möglich, nachdem wir in Zeile 1 das random-Modul importiert haben, das diese Funktion definiert.

import random

def get_result(n_self, n_other):
    result = (n_self - n_other) % 3
    if result == 0:
        return 'Das Spiel endete unentschieden.'
    elif result == 1:
        return 'Du hast gewonnen.'
    return 'Du hast leider verloren.'

objekte = ['Stein', 'Papier', 'Schere']
info_text = ('\n[0] Stein\n'
             '[1] Papier\n'
             '[2] Schere\n\n'
             'Gib eine Zahl zwischen 0 und 2 ein oder -1 zum Beenden: ')

while True:
    n_benutzer = int(input(info_text))
    if 0 <= n_benutzer <= 2:
        n_computer = random.randrange(3)
        print('-'*40)
        print(f'Benutzer: {objekte[n_benutzer]}')
        print(f'Computer: {objekte[n_computer]}')
        print(get_result(n_benutzer, n_computer))
        print('-'*40)
    elif n_benutzer == -1:
        break
    else:
        print('\n*** ungültige Eingabe\n')

Bereits in diese relativ kurzen Programm haben wir viele Aspekte einer Programmiersprache verwendet, die wir im Folgenden genauer besprechen werden. Dadurch dass das Beispiel nicht aus dem naturwissenschaftlichen Bereich gewählt war, kam allerdings ein Thema nicht zur Sprache, das uns ebenfalls noch beschäftigen wird. In den Natur- und Ingenieurwissenschaften haben die meisten Problemstellungen mit Zahlen zu tun, so dass sich Fragen stellen wie zum Beispiel wie groß der Bereich der Zahlen ist, die in einem Computer verarbeitet werden kann, oder ob die gewählte Programmiersprache komplexe Zahlen zulässt. Auch Vektoren oder Matrizen könnten von Interesse sein. In unserem Beispiel sieht man in Zeile 11 ein Objekt, das an einen Vektor erinnert.

objekte = ['Stein', 'Papier', 'Schere']
info_text = ('\n[0] Stein\n'
             '[1] Papier\n'
             '[2] Schere\n\n'
             'Gib eine Zahl zwischen 0 und 2 ein oder -1 zum Beenden: ')

Hierbei handelt es sich um eine Liste und es ist im Prinzip auch möglich, Listen von Zahlen zu verwenden. Allerdings sind Listen nicht geeignet, um Vektoren darzustellen und obwohl man Listen von Listen verwenden kann, eignen sich diese nicht zur Darstellung von Matrizen. An dieser Stelle greift man lieber auf das bereits in der Einleitung erwähnte NumPy-Paket zurück, das einem beispielsweise vielfältige Anwendungsmöglichkeiten im Bereich der linearen Algebra bietet.

Das hier besprochene Beispielprogramm war in erster Linie dazu gedacht, einige Programmierkonzepte zu illustrieren, die wir in den folgenden Kapiteln genauer besprechen wollen. Tatsächlich könnte man den Programmcode in verschiedener Hinsicht verbessern. Zwei Punkte wollen wir explizit ansprechen, da es sich lohnt, diese beim Programmieren im Hinterkopf zu behalten.

Einer der Punkte betrifft das zuvor besprochene Codesegment zwischen den Zeilen 11 und 15. Man sieht hier, dass die in der Liste objekte aufgeführten Zeichenketten in info_text wieder auftreten. Dies birgt die Gefahr, dass bei einer Änderung der Objektnamen in Zeile 11 übersehen wird, dass auch in den folgenden Zeilen eine Änderung vorzunehmen wäre. Es wäre also besser, den Text in info_text direkt aus den Informationen in objekte zu erzeugen.

Der zweite Punkt betrifft die Auswertung der Eingabe durch den Benutzer. Diese muss in eine ganze Zahl umwandelbar sein. Ansonsten bricht das Programm in Zeile 18 ab. Es empfiehlt sich, für solche Fälle vorzusorgen und dem Benutzer einen entsprechenden Hinweis auszugeben, wie dies in Zeile 29 der Fall ist, falls eine eingegebene Zahl nicht zwischen -1 und 2 liegt. Wie man solche Situationen sinnvoll behandelt, werden wir später noch genauer sehen.

---

[1]

Informationen zur phyphox-App sowie Links zum Herunterladen der App sind unter phyphox.org zu finden.

[2]

Auch wenn wir hier Kommas als Spaltentrenner benutzen, sind in CSV-Dateien auch andere Zeichen zu diesem Zwecke verwendbar, wie z.B. Semikolon oder Tabulatorzeichen.