3. Einfache Datentypen, Variablen und Zuweisungen

In Kapitel 2 hatten wir bereits verschiedene Datentypen kennengelernt. Hierzu gehören ganze Zahlen, die zum einen durch die explizite Umwandlung der Benutzereingabe in eine ganze Zahl oder als Ergebnis der randrange()-Funktion erzeugt wurden. Des Weiteren kamen Wahrheitswerte vor. Ganz explizit war dies bei True der Fall, das zur Konstruktion einer Dauerschleife verwendet wurde.

Diese beiden Datentypen, ganze Zahlen und Wahrheitswerte gehören zu den einfachen Datentypen. Daneben gibt es auch zusammengesetzte Datentypen, für die wir in Kapitel 2 ebenfalls schon Beispiele gesehen hatten. Dazu gehören die Zeichenketten, zum Beispiel in den Zeilen 12 bis 15 des Beispielprogramms, aber auch die durch eckige Klammern gekennzeichnete Liste in Zeile 11.

In diesem Kapitel werden wir uns zunächst den einfachen Datentypen zuwenden und die zusammengesetzten Datentypen in einem späteren Kapitel besprechen. Dabei werden wir vor allem neben den ganzen Zahlen noch weitere numerische Datentypen kennenlernen, die für natur- und ingenieurwissenschaftliche Anwendungen große Bedeutung besitzen.

3.1. Ganze Zahlen

Wir beginnen bei der Besprechung der numerischen Datentypen mit den ganzen Zahlen, auf Englisch integers. Auf den ersten Blick könnte man denken, dass in den Natur- und Ingenieurwissenschaften ganze Zahlen gegenüber den reellen Zahlen eigentlich unwichtig sind. Auch wenn diese Einschätzung nicht ganz falsch ist, verwenden wir auch in diesen Bereichen relativ oft ganze Zahlen, zum Beispiel als Index für eine Vektor- oder Matrixkomponente. Beim Programmieren spielen ganze Zahlen daher unter anderem eine große Rolle, sobald etwas gezählt oder indiziert werden muss. Eine weitere Anwendung ganzer Zahlen ergibt sich speziell in Python daraus, dass im Prinzip betragsmäßig beliebig große ganze Zahlen dargestellt werden können. Dies ermöglicht es, Rechnungen mit beliebiger Genauigkeit durchzuführen.

Die gerade angesprochene Frage, welche Zahlen überhaupt in einer Programmiersprache dargestellt werden können, ist von großer Bedeutung. Es lohnt sich daher, sich etwas genauer damit zu beschäftigen. Zahlen werden, wie andere Objekte auch, im Computer intern immer mit Hilfe von Nullen und Einsen dargestellt. Begrenzt man den Speicherplatz je Zahl, so ist der darstellbare Zahlenbereich eingeschränkt. Daher werden wir im Folgenden statt von »ganzen Zahlen«, die wir für das mathematische Objekt verwenden wollen, lieber von »Integers« sprechen, die sich auf die im Computer realisierbaren Zahlen beziehen.

Die Frage nach den im Computer darstellbaren Zahlen ist insofern wichtig, als ein Überschreiten des Zahlenbereichs zu Problemen führt. Bei den Gleitkommazahlen, die wir im nächsten Kapitel besprechen werden, führt eine begrenzte Zahl von Nachkommastellen zusätzlich zu dem Problem von Rundungsfehlern.

Doch kommen wir zurück zu den Integers. Wenn Python im Prinzip betragsmäßig beliebig große Zahlen erlaubt, könnte man meinen, dass man sich um die Größe des Zahlenbereichs nicht weiter kümmern muss. Das ist allerdings nicht ganz richtig. Zum einen ist jeder reale Computerspeicher begrenzt, so dass der Zahlenbereich letztlich doch eingeschränkt ist. In der Praxis spielt diese Einschränkung kaum eine Rolle, sondern eher die Zeit, die eine Rechenoperation mit sehr großen Integers benötigt. In anderen Programmiersprachen dagegen ist der Bereich der möglichen Integers eingeschränkt. Da die für uns wichtigen numerischen Programmbibliotheken NumPy und SciPy zu großen Teilen auf in C oder Fortran geschriebenen Programmen basieren, werden dort auch unter Python die Einschränkungen des Zahlenbereichs wichtig. Zu erwähnen wäre noch, dass die Integers, die als Index zur Adressierung in Listen oder Zeichenketten verwendet werden können, auch in Python beschränkt sind. Allerdings wird diese Beschränkung auf modernen Computern selten ein Problem darstellen.

Wie ganze Zahlen im Computer dargestellt werden und was das für die größenmäßige Einschränkung des Zahlenbereichs bedeutet, werden wir in einem Anhang in Kapitel 10 diskutieren. Dort werden auch die Grundlagen des Dualsystems erklärt, das der Darstellung von Zahlen mit Hilfe von Nullen und Einsen zugrunde liegt. Hier wollen wir uns nun stärker der praktischen Arbeit mit Integers zuwenden.

Als erstes wollen wir zeigen, dass Integers in Python tatsächlich sehr groß werden können, indem wir die tausendste Potenz von 2 ausrechnen lassen. Der doppelte Stern ** steht dabei für den Exponentierungsoperator.

2**1000

10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376

Das Ergebnis hat 302 Stellen. Genauso gut könnte man als Exponenten 100000 wählen und würde dann ein Ergebnis mit 30103 Stellen erhalten.

Natürlich gibt es neben positiven Integers auch solche mit negativem Vorzeichen.

2**100 - 2**101

-1267650600228229401496703205376

Die Leerzeichen um das Minuszeichen der Eingabe spielen für den Pythoninterpreter keine Rolle, sondern dienen hier der besseren Lesbarkeit.

In Python kann man auch mit Dual-, Oktal- und Hexadezimalzahlen arbeiten. Eine Einführung in Zahlensysteme, insbesondere das Dual- und das Hexadezimalsystem wird in Kapitel 10 gegeben. Um zwischen den verschiedenen Zahlensystemen unterscheiden zu können, werden Präfixe verwendet, und zwar 0b oder 0B für das Dualsystem, 0o oder 0O für das Oktalsystem sowie 0x oder 0X für das Hexadezimalsystem. Die folgenden drei Darstellungen sind jeweils äquivalent zur Zahl 25 im gewohnten Dezimalsystem

0b11001, 0o31, 0x19

(25, 25, 25)

Die Umwandlung in das Binär-, Oktal- oder Hexadezimalformat erfolgt mit Hilfe der Funktionen bin, oct bzw. hex:

bin(25), oct(25), hex(25)

('0b11001', '0o31', '0x19')

Das Ergebnis ist allerdings keine Zahl, sondern eine Zeichenkette, wie an den einschließenden Hochkommas zu erkennen ist.

Bei den meisten grundlegenden mathematischen Operationen wie Addition, Subtraktion, Multiplikation und Exponentiation ist gewährleistet, dass bei der Anwendung auf ganze Zahlen das Ergebnis wieder eine ganze Zahl ist. Eine Ausnahme ist die Division, da nicht klar ist, dass sich der Dividend durch den Divisor ohne Rest teilen lässt.

Um fehlerhafte Programme zu vermeiden, ist es daher wichtig zu wissen, wie die verwendete Programmiersprache die Division handhabt. Prinzipiell gibt es zwei Möglichkeiten. Eine Möglichkeit besteht darin, bei der Division von zwei ganzen Zahlen wieder eine ganze Zahl zu erzeugen und einen eventuell entstehenden Rest zu ignorieren. Bei der anderen Möglichkeit wird der Quotient als Gleitkommazahl dargestellt. Keine der beiden Varianten ist besser als die andere, so dass es für eine Programmiersprache auch keine natürliche Wahl gibt. Tatsächlich hat sich Python in der Version 2 an dieser Stelle anders verhalten als die Version 3, die wir heute benutzen.

Sehen wir uns an, wie Python 3 mit der Division von zwei Integers umgeht.

1/2

0.5

15/3

5.0

Offenbar wird hier immer eine Gleitkommazahl erzeugt, was an dem Dezimalpunkt ersichtlich ist. Dies gilt auch, wenn der Quotient wie im zweiten Fall im Prinzip als ganze Zahl darstellbar wäre.

Gelegentlich benötigt man aber eine Ganzzahldivision. In Python 3 erhält man diese mit einem doppelten Schrägstrich.

1//2

0

15//7

2

-15//7

-3

Frage

Was macht der //-Divisionsoperator in Python 3 tatsächlich, vor allem vor dem Hintergrund des letzten Beispiels? Warum dies so ist, lässt sich in einem Blog-Artikel von Guido van Rossum nachlesen.

Um zu verdeutlichen, dass die in Python 3 getroffene Wahl nicht zwingend ist, sehen wir uns zum Vergleich die Division in der Programmiersprache C an. Hier liefert

#include <stdio.h>

int main(void) {
  printf("%d %d\n", 15/7, -15/7);
}

als Ergebnis

2 -2

Im Gegensatz zu Python 3 führt in C die Division zweier Integers wieder auf einen Integer. Zudem wird hier zur Null hin abgeschnitten. Im zweiten Fall ergibt sich also nicht -3 wie bei Python 3, sondern -2. Genauso verhält sich auch der entsprechende Fortran-Code

program division
  write(*, *) 15/7, -15/7
  write(*, *) 1/2, 1.0/2
end program division

mit dem Ergebnis

           2          -2
           0  0.500000000

Die zweite Ausgabezeile illustriert, dass man hier eine Gleitkommadivision erzwingen kann, indem man mindestens eine der beiden Zahlen zu einer Gleitkommazahl macht.

Kommen wir nach diesem Ausflug zu anderen Programmiersprachen wieder zurück zu Python. Oft ist man am Rest einer Integerdivision interessiert. Diesen könnte man im Prinzip folgendermaßen erhalten

zaehler = 15
nenner = 4
rest = zaehler - (zaehler//nenner)*nenner
print(rest)

3

Mit Hilfe des Modulo-Operators % von Python geht dies jedoch einfacher.

zaehler = 15
nenner = 4
print(zaehler % nenner)

3

Eine häufige Anwendung ist der Test auf eine gerade oder ungerade Zahl.

16 % 2

0

Ist die Zahl ohne Rest durch 2 teilbar, ist sie offenbar gerade, ansonsten ungerade.

17 % 2

1

Benötigt man sowohl den Quotienten als auch den Rest, so kann man in Python beides in einem Schritt mit Hilfe der divmod()-Funktion erhalten

quotient, rest = divmod(42, 5)
print(quotient, rest)

8 2

Ein weiterer wichtiger Punkt, der hier für Integers zum ersten Mal auftritt, aber viel weitreichendere Bedeutung hat, ist die Reihenfolge, in der Operationen ausgeführt werden. In dem folgenden Beispiel sehen wir, dass in Python ebenso wie in C und Fortran die Regel Punkt vor Strich gilt.

2+3*4

14

Der Ausdruck wird also nicht von links nach rechts abgearbeitet. Möchte man zuerst die Addition ausführen, so muss man Klammern setzen.

(2+3)*4

20

Die wichtigsten für Python geltenden Vorrangregeln sind in der Tab. 3.1 dargestellt. Dabei haben die weiter oben stehenden Operationen Vorrang vor den nachfolgenden Operationen.

Tab. 3.1 Die weiter oben in der Liste stehenden Operationen haben Vorrang vor den weiter unten stehenden. Eine vollständige Liste findet man unter dem Punkt Operator precedence in der Python-Dokumentation. Beachten Sie, dass die dortige Tabelle umgekehrt geordnet ist, also weiter unten stehende Operatoren Vorrang haben.

Operatoren	Beschreibung
**	Exponentiation
+x, -x	Positives und negatives Vorzeichen
*, /, //, %	Multiplikation, Division, Modulo
+, -	Addition, Subtraktion

Wird der Exponentierungsoperator ** direkt von einem Plus oder Minus gefolgt, bindet das Vorzeichen allerdings stärker, was ja auch die einzig sinnvolle Interpretation dieses Codes ist.

2**-2

0.25

Dagegen ist das Ergebnis von

-2**2

-4

negativ.

Stehen Operatoren auf der gleichen Stufe, so wird der Ausdruck von links nach rechts ausgewertet. Gegebenenfalls müssen Klammern verwendet werden, um die gewünschte Reihenfolge sicherzustellen. Es spricht auch nichts dagegen, im Zweifelsfall oder zur besseren Lesbarkeit Klammern zu setzen, selbst wenn diese nicht zur korrekten Abarbeitung des Ausdrucks erforderlich sind.

Frage

Was ergibt -2*4+3**2? Was ergibt 6**4//2?

3.2. Gleitkommazahlen

Eine zentrale Rolle in der wissenschaftlichen Numerik spielen Gleitkommazahlen, die häufig auch mit dem englischen Begriff als Floats bezeichnet werden. Wir werden diesen Begriff gelegentlich verwenden, insbesondere um den Unterschied zum mathematischen Begriff der reellen Zahlen deutlich zu machen. Wesentlich ist dabei, dass sowohl der Zahlenbereich der Floats als auch die Zahl der Nachkommastellen begrenzt sind.

Während man sich beim normalen Rechnen per Hand üblicherweise keine Rechenschaft darüber ablegen muss, ob eine Zahl eine ganze Zahl oder eine Gleitkommazahl ist, ist dies beim numerischen Arbeiten anders. Im Kapitel 3.1 hatten wir ja schon gesehen, dass der Datentyp bei der Division durchaus eine Rolle spielen kann.

An dieser Stelle müssen wir wieder einmal auf Unterschiede zwischen Programmiersprachen hinweisen. In Sprachen wie C und Fortran muss der Datentyp einer Variable festgelegt werden. Das Fortranprogramm

program datentyp
  integer :: n
  real :: x

  n = 2
  x = n
  write(*, *) n, x
end program datentyp

erzeugt die Ausgabe

           2   2.00000000

Gemäß der Deklaration zu Beginn des Programms handelt es sich bei der Variable n um einen Integer, während x ein Float ist, der in Fortran mit real bezeichnet wird. In der hervorgehobenen Zeile findet bei der Zuweisung automatisch die Umwandlung zwischen den beiden Datentypen statt.

Im Gegensatz dazu ist eine Festlegung des Datentyps in Python nicht erforderlich. Man spricht in diesem Zusammenhang auch von duck typing: »If it looks like a duck and quacks like a duck, it must be a duck.« Kritiker halten dem entgegen, dass sich auch ein Drache scheinbar wie eine Ente verhalten kann.

Den Typ einer Variable kann man in Python mit Hilfe der type()-Funktion herausfinden.

n = 2
print(type(n))

<class 'int'>

Eine Umwandlung von einem Integer zu einem Float lässt sich in Python mit Hilfe der float()-Funktion vornehmen, wobei wir in diesem Beispiel gleich überprüfen, ob die Umwandlung tatsächlich stattgefunden hat.

x = float(n)
print(type(x))

<class 'float'>

Die umgekehrte Umwandlung von Floats in Integers ist mit der int()-Funktion möglich, wobei der Nachkommaanteil einfach abgeschnitten wird:

int(2.7)

2

Bereits das Anhängen eines Punktes genügt, damit Python die Zahl als Float interpretiert:

print(type(2.))

<class 'float'>

Für Floats gibt es zwei mögliche Schreibweisen. Zum einen die kann man die Dezimalbruchschreibweise verwenden, bei der ein Dezimalpunkt erwartet wird. Stehen vor oder nach dem Dezimalpunkt keine Ziffern, so wird der entsprechende Anteil gleich Null gesetzt.

5.

5.0

.25

0.25

Es ist aber nicht möglich, im Sinne einer abkürzenden Schreibweise sowohl vor als auch nach dem Dezimalpunkt auf Ziffern zu verzichten.

.

  Cell In[25], line 1
    .
    ^
SyntaxError: invalid syntax

Für sehr kleine oder sehr große Zahlen ist die Exponentialschreibweise besser geeignet. Die Zahl wird dabei mit Hilfe einer Mantisse, die nicht zwingend einen Dezimalpunkt enthalten muss, und einem ganzzahligen Exponenten, der ein Vorzeichen enthalten darf, dargestellt. Zwischen Mantisse und Exponenten muss dabei ein e oder ein E stehen.

1e-2

0.01

1.53e2

153.0

1E-5

1e-05

Da Dezimalzahlen im Allgemeinen keine endliche Binärdarstellung besitzen, kann es bei der Umwandlung in die Binärdarstellung zu Rundungsfehlern kommen. In Kapitel 10.1 wurde festgestellt, dass \(0{,}1_{10} = 0{,}0\overline{0011}_2\), so dass diese Zahl im Dualsystem auf jeden Fall abgeschnitten werden muss. Das Problem wird an dem folgenden Beispiel deutlich, das zudem zeigt, dass es auf die Reihenfolge der Operationen ankommen kann.

0.1+0.1+0.1-0.3

5.551115123125783e-17

0.1-0.3+0.1+0.1

2.7755575615628914e-17

Für die praktische Arbeit ist es wichtig, ein Gefühl dafür zu entwickeln, ob zum Beispiel eine von Null verschiedene Zahl ein wichtiger Effekt ist oder lediglich die Folge eines Rundungsfehlers.

Wie bereits gesagt, sind Floats in ihrer Größe begrenzt und sie können auch nicht beliebig dicht liegen. Informationen hierzu lassen sich in Python abfragen. Die größtmögliche Zahl, die sich als Float darstellen lässt lautet

import sys
sys.float_info.max

1.7976931348623157e+308

Die Distanz zwischen der 1 und der nächsten darauf folgenden darstellbaren Zahl ist

sys.float_info.epsilon

2.220446049250313e-16

Die kleinste normalisierte Zahl ist

sys.float_info.min

2.2250738585072014e-308

aber tatsächlich ist die kleinste darstellbare Zahl gleich 5e-324. Es gibt also um die Null herum eine Lücke, die jedoch deutlich kleiner ist als die Lücke zwischen der Eins und der darauf folgenden Zahl.

Hinweis

Seit Python 3.9 lässt sich die kleinste darstellbare Zahl, also 5e-324 mit Hilfe von math.ulp(0) erhalten.

Der Zahlenbereich für Floats sowie die Lücken um die Null und die Eins ergeben sich aus dem verwendeten Zahlenformat, das im IEEE-Standard 754 definiert ist. Einige Informationen dazu finden sich in Kapitel 11.

Im Gegensatz zu Integers können Gleitkommazahlen also nicht beliebig groß werden, sondern sind auf einen allerdings recht großzügig bemessenen Bereich bis etwas über \(10^{308}\) beschränkt. Sollte dieser Bereich sich als nicht ausreichend herausstellen, ist es empfehlenswert, sich zunächst einmal Gedanken darüber zu machen, ob man das verwendete numerische Verfahren geeignet formuliert hat. Eventuell kann schon eine Skalierung der Variablen das Problem beseitigen. Im schlimmsten Fall kann man in Python zum mpmath-Modul greifen, das es erlaubt, mit mehr als den standardmäßigen 15 signifikanten Stellen zu rechnen.

Was passiert aber, wenn man den zulässigen Zahlenbereich von Floats überschreitet? In diesem Fall setzt Python die entsprechende Zahl auf Unendlich oder inf vom vom englischen infinity.

sys.float_info.max*1.00000001

inf

Dieses Unendlich ist zudem vorzeichenbehaftet.

-sys.float_info.max*1.00000001

-inf

In manchen Situation kann man mit dem Ergebnis sogar noch weiterrechnen.

x = sys.float_info.max*1.00000001
print(1/x)

0.0

Dies ist jedoch nicht der Fall, wenn man zweimal positiv Unendlich voneinander abziehen will.

1e400 - 1e401

nan

Hierbei steht nan für »not a number«.

Anders als man nach dieser Diskussion vielleicht denke könnte, hat eine Division durch Null nicht das Ergebnis inf. Vielmehr gibt es einen ZeroDivisionError.

1.5/0

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
Cell In[38], line 1
----> 1 1.5/0

ZeroDivisionError: float division by zero

Hierbei handelt es sich um eine so genannte Ausnahme oder Englisch exception, die man geeignet behandeln kann, wie wir später noch sehen werden.

3.3. Funktionen für reelle Zahlen

In numerischen Anwendungen in den Natur- und Ingenieurwissenschaften wird man häufig mathematische Funktionen auswerten wollen. Der Versuch, beispielsweise eine Exponentialfunktion auszuwerten, führt jedoch nicht unmittelbar zum Erfolg.

exp(2)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[39], line 1
----> 1 exp(2)

NameError: name 'exp' is not defined

Hierfür kann es im Wesentlichen zwei Gründe geben. Entweder hat die Exponentialfunktion nicht den Namen exp oder die Exponentialfunktion ist nicht verfügbar, zumindest nicht so unmittelbar, wie wir das hier annehmen. Tatsächlich muss man in Python, genauso wie in C, ein klein wenig mehr tun, als nur die Exponentialfunktion aufzurufen.

Bevor wir uns das gleich genauer ansehen, wollen wir kurz auf zwei für das wissenschaftliche Rechnen relevante Programmiersprachen hinweisen, bei denen die Exponentialfunktion sowie eine ganze Reihe weiterer mathematischer Funktionen direkt aufgerufen werden können. Eine dieser Sprachen ist Fortran, eine relativ alte, aber im wissenschaftlichen Bereich immer noch häufig eingesetzte Sprache, deren Name ursprünglich als Abkürzung für »Formula Translation« stand. Damit kann man schon erwarten, dass sich in Fortran mathematische Funktionen sehr einfach verwenden lassen.

Eine moderne Sprache, in der dies ebenfalls der Fall ist, ist Julia. Hierbei handelt es sich wie bei Python um eine interpretierte Sprache, so dass wir die Exponentiation einfach in der Julia-Shell ausprobieren können.

$ julia
               _
   _       _ _(_)_     |  Documentation: https://docs.julialang.org
  (_)     | (_) (_)    |
   _ _   _| |_  __ _   |  Type "?" for help, "]?" for Pkg help.
  | | | | | | |/ _` |  |
  | | |_| | | | (_| |  |  Version 1.9.2 (2023-07-05)
 _/ |\__'_|_|_|\__'_|  |  https://github.com/conda-forge/julia-feedstock
|__/                   |

julia> exp(2)
7.38905609893065

Wesentlich komplizierter ist das Vorgehen in Python allerdings auch nicht. Man muss nur daran denken, zunächst das Modul math, das Bestandteil der Python-Standardbibliothek ist zu laden.

import math
math.exp(2)

7.38905609893065

Zum Vergleich mit Python betrachten wir den folgenden Code, der die Verwendung einer mathematischen Funktion in der Programmiersprache C illustriert:

#include <stdio.h>
#include <math.h>

int main(void) {
  double x = 2;
  printf("Die Exponentialfunktion von %f ist %f\n", x, exp(x));
}

Hier entspricht die hervorgehobene Zeile dem import-Befehl in Python. Zudem muss man beim Kompilieren, also der Übersetzung des Programms in maschinenlesbaren Code mit -lm noch die Mathematikbibliothek hinzuzulinken.

$ cc -o bsp_exp bsp_exp.c -lm
$ ./bsp_exp
Die Exponentialfunktion von 2.000000 ist 7.389056

In der ersten Zeile wird mit -o bsp_exp festgelegt, dass die Ausgabedatei den Namen bsp_exp heißen soll. Diese wird in der zweiten Zeile ausgeführt und wir erhalten in der dritten Zeile die erwartete Ausgabe.

Weiterführendes (rechts aufklappen)

Nach der Kompilierung des obigen C-Programms entsteht als Zwischenprodukt ein so genanntes Assembler-Programm, das schon sehr maschinennah ist und von einem Assembler in den von einem Computer les- und ausführbaren Maschinencode umgewandelt wird.

            .file   "bsp_exp.c"
            .text
            .section        .rodata
            .align 8
    .LC1:
            .string "Die Exponentialfunktion von %f ist %f\n"
            .text
            .globl  main
            .type   main, @function
    main:
    .LFB0:
            .cfi_startproc
            pushq   %rbp
            .cfi_def_cfa_offset 16
            .cfi_offset 6, -16
            movq    %rsp, %rbp
            .cfi_def_cfa_register 6
            subq    $32, %rsp
            movsd   .LC0(%rip), %xmm0
            movsd   %xmm0, -8(%rbp)
            movq    -8(%rbp), %rax
            movq    %rax, -24(%rbp)
            movsd   -24(%rbp), %xmm0
            call    exp@PLT
            movq    -8(%rbp), %rax
            movapd  %xmm0, %xmm1
            movq    %rax, -24(%rbp)
            movsd   -24(%rbp), %xmm0
            leaq    .LC1(%rip), %rdi
            movl    $2, %eax
            call    printf@PLT
            movl    $0, %eax
            leave
            .cfi_def_cfa 7, 8
            ret
            .cfi_endproc
    .LFE0:
            .size   main, .-main
            .section        .rodata
            .align 8
    .LC0:
            .long   0
            .long   1073741824
            .ident  "GCC: (Ubuntu 7.5.0-3ubuntu1~18.04) 7.5.0"
            .section        .note.GNU-stack,"",@progbits

Kommen wir nach diesem Ausflug in andere Programmiersprachen zurück zum Import von Funktionen aus dem math-Modul der Python-Standardbibliothek. Die obige Form des Imports ist nur eine von mehrere möglichen Varianten, die Vor- und Nachteile haben.

In der ersten Variante, die wir weiter oben verwendet haben, wird das Modul, hier math dem eigenen Code bekannt gemacht. Dies geschieht in unserem Beispiel mit import math. Der Nachteil hiervon ist, dass man jedes Mal, wenn man sich auf ein Objekt aus dem Modul beziehen will, den Modulnamen voranstellen muss. Deswegen mussten wir math.exp schreiben. Diese Mehrarbeit lohnt sich aber unter Umständen, um im Code deutlich zu machen, aus welchem Modul zum Beispiel eine Funktion stammt.

Alternativ hierzu kann man bestimmte Objekte, also Funktionen oder auch Attribute, importieren. Diese stehen dann wie in dem folgenden Beispiel zur Verfügung, ohne dass der Modulname voranzustellen ist.

from math import sin, cos
sin(0.5)**2+cos(0.5)**2

1.0

Schließlich gibt es noch die Möglichkeit, sämtliche Objekte eines Moduls auf einmal einbinden

from math import *
log(10)

2.302585092994046

Dieses Vorgehen ist allerdings nicht ganz unproblematisch, da man auf diese Weise einen unter Umständen großen Namensraum einbindet und damit potentiell unabsichtlich Funktionen definiert oder umdefiniert, wodurch die Funktion des Programms beeinträchtigt werden kann. Einer solchen Situation werden wir im nächsten Abschnitt noch begegnen.

Jetzt wollen wir uns aber zunächst einen Überblick über die Funktionalität verschaffen, die uns das math-Modul zur Verfügung stellt. Nachdem wir das Modul schon weiter oben importiert haben, können wir uns eine Hilfetext ausgeben lassen, der alle definierten Funktionen und Konstanten zusammen mit einem erläuternden Text aufführt. Wir werden im Folgenden einige Aspekte diskutieren. Zuvor können Sie sich aber gerne anhand des Hilfetextes einen ersten Überblick über die Möglichkeiten verschaffen, die das math-Modul bietet. Beachten Sie dabei, dass das Modul im Laufe der Zeit weiterentwickelt wird. Es kann also sein, dass einzelne Funktionen in älteren Python-Versionen noch nicht vorhanden sind.

help(math)

Help on module math:

NAME
    math

MODULE REFERENCE
    https://docs.python.org/3.11/library/math.html
    
    The following documentation is automatically generated from the Python
    source files.  It may be incomplete, incorrect or include features that
    are considered implementation detail and may vary between Python
    implementations.  When in doubt, consult the module reference at the
    location listed above.

DESCRIPTION
    This module provides access to the mathematical functions
    defined by the C standard.

FUNCTIONS
    acos(x, /)
        Return the arc cosine (measured in radians) of x.
        
        The result is between 0 and pi.
    
    acosh(x, /)
        Return the inverse hyperbolic cosine of x.
    
    asin(x, /)
        Return the arc sine (measured in radians) of x.
        
        The result is between -pi/2 and pi/2.
    
    asinh(x, /)
        Return the inverse hyperbolic sine of x.
    
    atan(x, /)
        Return the arc tangent (measured in radians) of x.
        
        The result is between -pi/2 and pi/2.
    
    atan2(y, x, /)
        Return the arc tangent (measured in radians) of y/x.
        
        Unlike atan(y/x), the signs of both x and y are considered.
    
    atanh(x, /)
        Return the inverse hyperbolic tangent of x.
    
    cbrt(x, /)
        Return the cube root of x.
    
    ceil(x, /)
        Return the ceiling of x as an Integral.
        
        This is the smallest integer >= x.
    
    comb(n, k, /)
        Number of ways to choose k items from n items without repetition and without order.
        
        Evaluates to n! / (k! * (n - k)!) when k <= n and evaluates
        to zero when k > n.
        
        Also called the binomial coefficient because it is equivalent
        to the coefficient of k-th term in polynomial expansion of the
        expression (1 + x)**n.
        
        Raises TypeError if either of the arguments are not integers.
        Raises ValueError if either of the arguments are negative.
    
    copysign(x, y, /)
        Return a float with the magnitude (absolute value) of x but the sign of y.
        
        On platforms that support signed zeros, copysign(1.0, -0.0)
        returns -1.0.
    
    cos(x, /)
        Return the cosine of x (measured in radians).
    
    cosh(x, /)
        Return the hyperbolic cosine of x.
    
    degrees(x, /)
        Convert angle x from radians to degrees.
    
    dist(p, q, /)
        Return the Euclidean distance between two points p and q.
        
        The points should be specified as sequences (or iterables) of
        coordinates.  Both inputs must have the same dimension.
        
        Roughly equivalent to:
            sqrt(sum((px - qx) ** 2.0 for px, qx in zip(p, q)))
    
    erf(x, /)
        Error function at x.
    
    erfc(x, /)
        Complementary error function at x.
    
    exp(x, /)
        Return e raised to the power of x.
    
    exp2(x, /)
        Return 2 raised to the power of x.
    
    expm1(x, /)
        Return exp(x)-1.
        
        This function avoids the loss of precision involved in the direct evaluation of exp(x)-1 for small x.
    
    fabs(x, /)
        Return the absolute value of the float x.
    
    factorial(n, /)
        Find n!.
        
        Raise a ValueError if x is negative or non-integral.
    
    floor(x, /)
        Return the floor of x as an Integral.
        
        This is the largest integer <= x.
    
    fmod(x, y, /)
        Return fmod(x, y), according to platform C.
        
        x % y may differ.
    
    frexp(x, /)
        Return the mantissa and exponent of x, as pair (m, e).
        
        m is a float and e is an int, such that x = m * 2.**e.
        If x is 0, m and e are both 0.  Else 0.5 <= abs(m) < 1.0.
    
    fsum(seq, /)
        Return an accurate floating point sum of values in the iterable seq.
        
        Assumes IEEE-754 floating point arithmetic.
    
    gamma(x, /)
        Gamma function at x.
    
    gcd(*integers)
        Greatest Common Divisor.
    
    hypot(...)
        hypot(*coordinates) -> value
        
        Multidimensional Euclidean distance from the origin to a point.
        
        Roughly equivalent to:
            sqrt(sum(x**2 for x in coordinates))
        
        For a two dimensional point (x, y), gives the hypotenuse
        using the Pythagorean theorem:  sqrt(x*x + y*y).
        
        For example, the hypotenuse of a 3/4/5 right triangle is:
        
            >>> hypot(3.0, 4.0)
            5.0
    
    isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0)
        Determine whether two floating point numbers are close in value.
        
          rel_tol
            maximum difference for being considered "close", relative to the
            magnitude of the input values
          abs_tol
            maximum difference for being considered "close", regardless of the
            magnitude of the input values
        
        Return True if a is close in value to b, and False otherwise.
        
        For the values to be considered close, the difference between them
        must be smaller than at least one of the tolerances.
        
        -inf, inf and NaN behave similarly to the IEEE 754 Standard.  That
        is, NaN is not close to anything, even itself.  inf and -inf are
        only close to themselves.
    
    isfinite(x, /)
        Return True if x is neither an infinity nor a NaN, and False otherwise.
    
    isinf(x, /)
        Return True if x is a positive or negative infinity, and False otherwise.
    
    isnan(x, /)
        Return True if x is a NaN (not a number), and False otherwise.
    
    isqrt(n, /)
        Return the integer part of the square root of the input.
    
    lcm(*integers)
        Least Common Multiple.
    
    ldexp(x, i, /)
        Return x * (2**i).
        
        This is essentially the inverse of frexp().
    
    lgamma(x, /)
        Natural logarithm of absolute value of Gamma function at x.
    
    log(...)
        log(x, [base=math.e])
        Return the logarithm of x to the given base.
        
        If the base not specified, returns the natural logarithm (base e) of x.
    
    log10(x, /)
        Return the base 10 logarithm of x.
    
    log1p(x, /)
        Return the natural logarithm of 1+x (base e).
        
        The result is computed in a way which is accurate for x near zero.
    
    log2(x, /)
        Return the base 2 logarithm of x.
    
    modf(x, /)
        Return the fractional and integer parts of x.
        
        Both results carry the sign of x and are floats.
    
    nextafter(x, y, /)
        Return the next floating-point value after x towards y.
    
    perm(n, k=None, /)
        Number of ways to choose k items from n items without repetition and with order.
        
        Evaluates to n! / (n - k)! when k <= n and evaluates
        to zero when k > n.
        
        If k is not specified or is None, then k defaults to n
        and the function returns n!.
        
        Raises TypeError if either of the arguments are not integers.
        Raises ValueError if either of the arguments are negative.
    
    pow(x, y, /)
        Return x**y (x to the power of y).
    
    prod(iterable, /, *, start=1)
        Calculate the product of all the elements in the input iterable.
        
        The default start value for the product is 1.
        
        When the iterable is empty, return the start value.  This function is
        intended specifically for use with numeric values and may reject
        non-numeric types.
    
    radians(x, /)
        Convert angle x from degrees to radians.
    
    remainder(x, y, /)
        Difference between x and the closest integer multiple of y.
        
        Return x - n*y where n*y is the closest integer multiple of y.
        In the case where x is exactly halfway between two multiples of
        y, the nearest even value of n is used. The result is always exact.
    
    sin(x, /)
        Return the sine of x (measured in radians).
    
    sinh(x, /)
        Return the hyperbolic sine of x.
    
    sqrt(x, /)
        Return the square root of x.
    
    tan(x, /)
        Return the tangent of x (measured in radians).
    
    tanh(x, /)
        Return the hyperbolic tangent of x.
    
    trunc(x, /)
        Truncates the Real x to the nearest Integral toward 0.
        
        Uses the __trunc__ magic method.
    
    ulp(x, /)
        Return the value of the least significant bit of the float x.

DATA
    e = 2.718281828459045
    inf = inf
    nan = nan
    pi = 3.141592653589793
    tau = 6.283185307179586

FILE
    /usr/share/miniconda/lib/python3.11/lib-dynload/math.cpython-311-x86_64-linux-gnu.so

Zunächst stellen wir fest, dass die wichtigsten Funktionsklassen wie trigonometrische und hyperbolische Funktionen sowie ihre Inversen, Logarithmen und die Exponentialfunktion vorhanden sind. Hinzu kommt noch eine kleine Zahl speziellere Funktionen wie die Gamma- oder die Fehlerfunktion. Für andere spezielle Funktionen, beispielsweise Besselfunktionen, steht die numerische Bibliothek SciPy zur Verfügung.

Bei den trigonometrischen Funktionen muss man sich immer die Frage stellen, ob Winkel im Bogenmaß oder in Grad erwartet werden. Die trigonometrischen Funktionen aus dem math-Modul erwarten Argumente im Bogenmaß.

from math import sin, pi
sin(90), sin(0.5*pi)

(0.8939966636005579, 1.0)

Tipp

Python stellt mit math.tau auch die Konstante 2π zur Verfügung, die gelegentlich als fundamentalere Zahl angesehen wird.

Wie man sieht, liefert das Argument in Grad nicht das vielleicht erwartete Ergebnis 1. Anders ist dies, wenn man das Argument im Bogenmaß einsetzt. In diesem Beispiel haben wir übrigens auch ausgenutzt, dass das math-Modul einige konstanten definiert, unter anderem eben die Kreiszahl π und die eulersche Zahl e.

Die Umrechnung zwischen Bogenmaß und Grad kann explizit mit einem Faktor 180/π vornehmen oder die Funktionen degrees() und radians() heranziehen. Letzteres kann für die Lesbarkeit hilfreich sein. Damit können wir unser obiges Beispiel für Argumente in Grad anpassen.

from math import radians
sin(radians(90))

1.0

Hinweis

Die Funktion sin() hatten wir bereits weiter oben importiert und brauchen dies daher hier nicht mehr zu tun. In einem größeren Programm würde man normalerweise alle benötigten import-Anweisungen an den Anfang des Programms stellen.

Bei der Umrechnung zwischen kartesischen und Polarkoordinaten, deren Beziehung durch

\[\begin{split}\begin{align} x &= r\cos(\varphi)\\ y &= r\sin(\varphi) \end{align}\end{split}\]

gegeben ist, kann man den Arkustangens verwenden, um den zu den kartesischen Koordinaten \((x,y)\) gehörigen Winkel

\[\varphi = \arctan\left(\frac{y}{x}\right)\]

zu berechnen. Dazu muss man zunächst einmal wissen, dass der Arkustangens in Python durch die Funktion atan() berechnet wird.

from math import atan, degrees, sqrt
x = 1
y = sqrt(3)
degrees(atan(y/x))

59.99999999999999

Wir erhalten also, bis auf einen Rundungsfehler, den erwarteten Winkel von \(60^\circ\).

Allerdings gibt es zwei Probleme. Zum einen kann der Punkt auf der \(y\)-Achse liegen.

x = 0
y = 1
atan(y/x)

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
Cell In[47], line 3
      1 x = 0
      2 y = 1
----> 3 atan(y/x)

ZeroDivisionError: division by zero

Hier kommt es überhaupt nicht zur Berechnung des Arkustangens, da schon die Division fehlschlägt. Das andere Probleme besteht darin, dass man nicht zwischen einem Punkt und dem am Ursprung gespiegelten Punkt unterscheiden kann.

x = -1
y = -sqrt(3)
degrees(atan(y/x))

59.99999999999999

Obwohl der Punkt im dritten Quadranten liegt, erhalten wir wieder das Ergebnis \(60^\circ\), während das korrekte Ergebnis \(240^\circ\) wäre.

Für solche Fälle stellt Python die Funktion atan2() zur Verfügung.

from math import atan2
help(atan2)

Help on built-in function atan2 in module math:

atan2(y, x, /)
    Return the arc tangent (measured in radians) of y/x.
    
    Unlike atan(y/x), the signs of both x and y are considered.

Wichtig ist hier, dass das erste Argument der Zahl entspricht, die normalerweise im Zähler des Bruches stehen würde, bei uns also y. Unsere Beispiel würde dann folgendermaßen aussehen:

x = 0
y = 1
degrees(atan2(y, x))

90.0

x = -1
y = -sqrt(3)
degrees(atan2(y, x))

-120.00000000000001

Wir erhalten also die erwarteten Ergebnisse, da \(-120^\circ\) äquivalent zu \(240^\circ\) ist.

Im Zusammenhang mit der Umrechnung zwischen kartesischen und Polarkoordinaten hat man bei der Berechnung des Abstands

\[r = \sqrt{x^2+y^2}\]

die Wahl, diesen Ausdruck explizit hinzuschreiben oder die in Python vorhandene hypot()-Funktion zu verwenden. Letzteres kann unter anderem dazu dienen, den Code lesbarer zu machen.

x = 1
y = 2
sqrt(x**2 + y**2), hypot(x, y)

(2.23606797749979, 2.23606797749979)

Der Name dieser Funktion erklärt sich daraus, dass hier die Länge der Hypothenuse berechnet wird. Verwandt hiermit ist die dist()-Funktion, die den Abstand zweier Punkte berechnet. Sowohl dist() als auch hypot() funktionieren auch in mehr als zwei Dimensionen.

from math import dist
dist((1, 2, 3), (2, 1, 4))

1.7320508075688772

In diesem Beispiel ergibt sich wie erwartet die Wurzel aus 3.

Hinweis

Die Verwendung von dist() sowie von hypot() in mehr als zwei Dimensionen erfordert mindestens Python 3.8.

Eine weitere wichtige Klasse von Funktionen, die vom math-Modul zur Verfügung gestellt werden, sind die Logarithmen und die Exponentialfunktion. Hier muss man vor allem zwischen dem natürlichen Logarithmus, der häufig als „ln‟ geschrieben wird, und dem Zehner- oder dekadischen Logarithmus unterscheiden. In Python wird der natürliche Logarithmus mit Hilfe der log()-Funktion berechnet und für den dekadischen Logarithmus gibt es die log10()-Funktion. Die gleiche Namensbezeichnungen werden zum Beispiel in C, Fortran und Julia verwendet.

from math import e, log, log10
log(e**2), log10(10**-3)

(2.0, -3.0)

Hinweis

Die log()-Funktion akzeptiert noch ein zweites Argument, das dann die Basis angibt. Damit könnte man den dekadischen Logarithmus auch mit log(x, 10) berechnen, was aber potentiell ungenauer ist als log10(x).

Neben dem natürlichen Logarithmus log() und der Exponentialfunktion exp() stellt Python auch noch die Funktionen log1p() und expm1() zur Verfügung. Wozu diese beiden Funktionen erforderlich sind, wollen wir uns nun ansehen.

Mathematisch stellen Quotienten zweier Funktionen ein Problem dar, wenn sie auf einen Ausdruck der Form \(0/0\) führen. Man muss dann eine geeignete Grenzwertbildung durchführen oder kann zum Beispiel den Satz von l’Hôpital anwenden. Numerisch wird das Problem noch dadurch schwieriger, dass Gleitkommazahlen nach einer gewissen Anzahl von Nachkommastellen abgeschnitten werden.

Wenn wir also beispielsweise den Grenzwert

\[\lim_{x\to 0} \frac{\mathrm{e}^x-1}{x}\]

numerisch bestimmen wollen, kann es für kleine Werte von \(x\) zu Problemen kommen. Wir könnten zwar für hinreichend kleine Werte von \(x\) den Zähler mit Hilfe der Taylorreihe für die Exponentialfunktion

\[\mathrm{e}^x = \sum_{n=0}^\infty\frac{x^n}{n!}\]

annähern, aber die expm1()-Funktion nimmt uns diese Arbeit ab.

from math import expm1
x = 0.00001
exp(x)-1, expm1(x)

(1.0000050000069649e-05, 1.0000050000166668e-05)

Mit Hilfe der führenden Terme der zugehörigen Taylorreihe wird deutlich, dass das Resultat der expm1()-Funktion das richtige ist. Die weiteren Terme sind zu klein, um einen Unterschied zu machen, und da sie positiv sind, würden Sie den Abstand zum Resultat der exp()-Funktion ohnehin nur weiter vergrößern.

x = 0.00001
x + x**2/2 + x**3/6

1.0000050000166668e-05

In Abb. 3.1 ist der Unterschied der beiden Berechnungsweisen als Funktion von x zu sehen. Die durchgezogene Linie ist mit der expm1()-Funktion berechnet. Sie läuft in korrekter Weise gegen den Grenzwerten, was man in dieser Auftragung daran sieht, dass die Abweichung \(f(x)-1\) vom Grenzwert gegen Null geht. Die blauen Punkte sind dagegen mit der exp()-Funktion berechnet. Hier sieht man deutliche Abweichungen unterhalb von \(x \lesssim 10^{-8}\), die in der Praxis das gesuchte Ergebnis unter Umständen entscheidend verfälschen könnten.

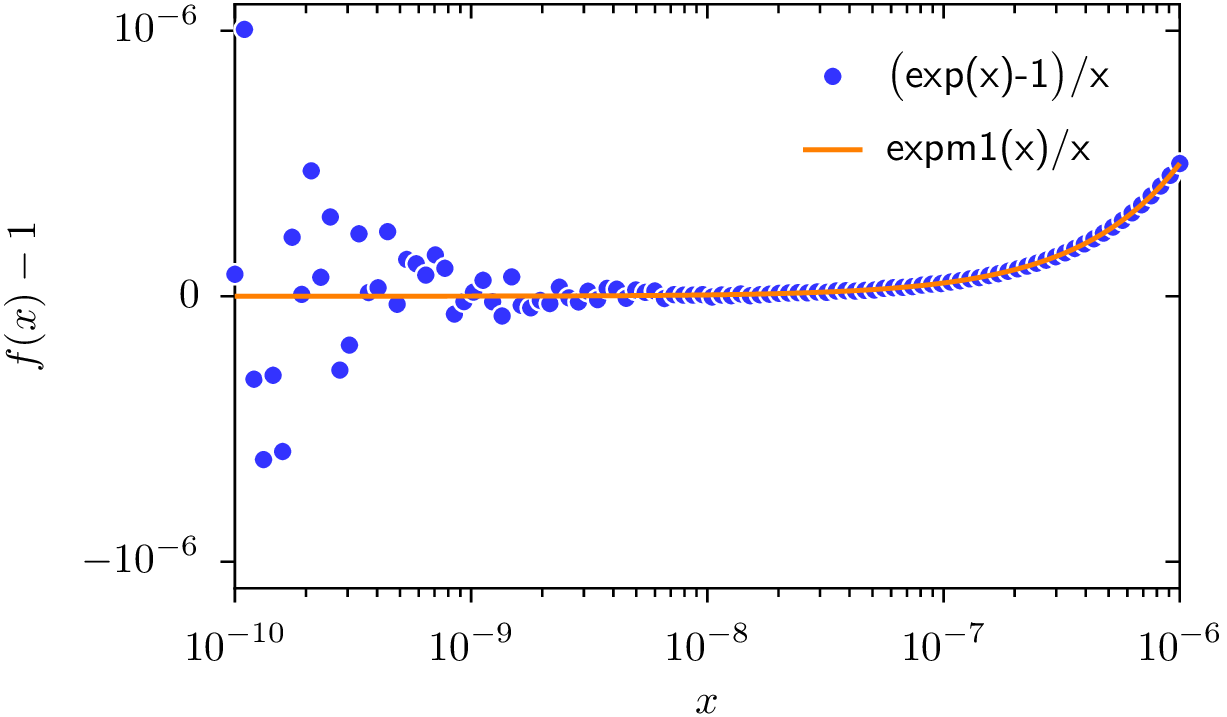
Abb. 3.1 Vergleich von exp(x)-1 (Punkte) und expm1(x) (durchgezogene Linie) durch Betrachtung des Grenzwerts von \(f(x) = (\mathrm{e}^x-1)/x\).

Der Logarithmus geht für das Argument 1 durch Null, so dass dort Argumente in der Nähe von 1 einer besonderen Behandlung bedürfen. Hierzu steht in Python für den natürlichen Logarithmus die Funktion log1p() zur Verfügung.

from math import log1p
x = 1e-5
log(1+x), log1p(x)

(9.999950000398841e-06, 9.999950000333332e-06)

Auch hier kann man sich durch Auswertung der führenden Term der Taylorreihe von

\[\log(1+x) = \sum_{n=1}^\infty\frac{(-1)^{n+1}x^n}{n}\]

davon überzeugen, dass log1p() bis auf Rundungsfehler den korrekten Wert liefert.

x = 1e-5
x - x**2/2 + x**3/3

9.999950000333334e-06

3.4. Komplexe Zahlen

Neben reellen Zahlen benötigt man immer wieder auch komplexe Zahlen. Dabei erzeugt man einen Imaginärteil durch Anhängen des Buchstabens j oder J, das Ingenieure häufig statt des in der Mathematik und Physik üblichen i verwenden.

(1+0.5j)/(1-0.5j)

(0.6+0.8j)

Alternativ kann man die Funktion complex() verwenden.

z1 = complex(1, 0.5)
z2 = complex(1, -0.5)
z1/z2

(0.6+0.8j)

Möchte man aus den Werten zweier Variablen eine komplexe Zahl konstruieren, geht dies mit der zweiten der gerade genannten Methoden sehr einfach

x = 1
y = 2
z1 = complex(x, y)
z2 = complex(x, -y)
z1/z2

(-0.6+0.8j)

Falls man die Funktion complex() nicht verwenden möchte, muss man beachten, dass die folgenden beiden Wege nicht zum Ziel führen.

x = 18
y = 9
z = x+yj

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[62], line 3
      1 x = 18
      2 y = 9
----> 3 z = x+yj

NameError: name 'yj' is not defined

Hier geht Python davon aus, dass es sich bei yj um eine Variable handelt, der aber noch kein Wert zugewiesen wurde, die also noch nicht definiert ist, wie Python in der Fehlermeldung sagt. Dies lässt sich leicht überprüfen, wenn man neben x, dem wir schon den Wert 18 zugewiesen haben, noch einen Wert für yj setzt.

yj = 24
x+yj

42

Genauso verhält es sich, wenn wir versuchen, die Variable y, die den Imaginärteil repräsentieren soll, mit j zu multiplizieren. j würde von Python wieder als noch undefinierte Variable angesehen und so erklärt sich dann auch die Fehlermeldung.

z = x+y*j

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[64], line 1
----> 1 z = x+y*j

NameError: name 'j' is not defined

Vielmehr muss die imaginäre Einheit explizit als 1j geschrieben werden. Den Grund hierfür werden wir noch genauer verstehen, wenn wir in Kapitel 3.5 besprechen, welche Namen für Variablen zugelassen sind.

z = x+y*1j
z

(18+9j)

Das Resultat für z ergibt sich aus den weiter oben definierten Werten von x und y.

Aufgabe

Zeigen Sie an einem oder mehreren Beispielen, dass das Ergebnis einer Rechnung, die komplexe Zahlen enthält, selbst dann als komplexe Zahl dargestellt wird, wenn das Ergebnis reell ist.

Hat man eine komplexe Zahl einer Variablen zugewiesen, wie wir dies in Kapitel 3.5 noch genauer diskutieren werden, so lassen sich aus der Variablen wieder der Real- und der Imaginärteil extrahieren.

x = 1+0.5j
x.real, x.imag

(1.0, 0.5)

Man kann sich auch die konjugiert komplexe Zahl beschaffen.

x.conjugate()

(1-0.5j)

Die Unterschiede in den Aufrufen ergeben sich daraus, dass bei Real- und Imaginärteil auf Attribute, also Eigenschaften, der komplexen Zahl zugegriffen wird, während bei der komplexen Konjugation eine Methode aufgerufen wird, die etwas mit der komplexen Zahl macht. Es mag an dieser Stelle verwirren, dass man nicht alternativ conjugate(x) verwenden kann. Die Hintergründe werden im Kapitel 9 klarer werden, wo wir uns mit dem objektorientierten Programmieren beschäftigen werden.

Natürlich wollen wir auch für komplexe Zahlen mathematische Funktionen auswerten. Das Modul math hilft hier aber leider nicht weiter, da es nur mit reellen Zahlen umgehen kann und erfolglos versucht, das komplexe Argument in eine reelle Zahl umzuwandeln. Python wäre durchaus in der Lage, eine reelle Zahl in eine komplexe Zahl umzuwandeln, aber für den umgekehrten Weg gibt es keine mathematisch eindeutige Vorschrift, die Python verwenden könnte.

from math import exp, pi
exp(0.25j*pi)

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[68], line 2
      1 from math import exp, pi
----> 2 exp(0.25j*pi)

TypeError: must be real number, not complex

Es gibt jedoch in der Python-Standardbibliothek ein Modul cmath, das mit komplexen Zahlen umgehen kann.

import cmath
help(cmath)

Help on module cmath:

NAME
    cmath

MODULE REFERENCE
    https://docs.python.org/3.11/library/cmath.html
    
    The following documentation is automatically generated from the Python
    source files.  It may be incomplete, incorrect or include features that
    are considered implementation detail and may vary between Python
    implementations.  When in doubt, consult the module reference at the
    location listed above.

DESCRIPTION
    This module provides access to mathematical functions for complex
    numbers.

FUNCTIONS
    acos(z, /)
        Return the arc cosine of z.
    
    acosh(z, /)
        Return the inverse hyperbolic cosine of z.
    
    asin(z, /)
        Return the arc sine of z.
    
    asinh(z, /)
        Return the inverse hyperbolic sine of z.
    
    atan(z, /)
        Return the arc tangent of z.
    
    atanh(z, /)
        Return the inverse hyperbolic tangent of z.
    
    cos(z, /)
        Return the cosine of z.
    
    cosh(z, /)
        Return the hyperbolic cosine of z.
    
    exp(z, /)
        Return the exponential value e**z.
    
    isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0)
        Determine whether two complex numbers are close in value.
        
          rel_tol
            maximum difference for being considered "close", relative to the
            magnitude of the input values
          abs_tol
            maximum difference for being considered "close", regardless of the
            magnitude of the input values
        
        Return True if a is close in value to b, and False otherwise.
        
        For the values to be considered close, the difference between them must be
        smaller than at least one of the tolerances.
        
        -inf, inf and NaN behave similarly to the IEEE 754 Standard. That is, NaN is
        not close to anything, even itself. inf and -inf are only close to themselves.
    
    isfinite(z, /)
        Return True if both the real and imaginary parts of z are finite, else False.
    
    isinf(z, /)
        Checks if the real or imaginary part of z is infinite.
    
    isnan(z, /)
        Checks if the real or imaginary part of z not a number (NaN).
    
    log(...)
        log(z[, base]) -> the logarithm of z to the given base.
        
        If the base not specified, returns the natural logarithm (base e) of z.
    
    log10(z, /)
        Return the base-10 logarithm of z.
    
    phase(z, /)
        Return argument, also known as the phase angle, of a complex.
    
    polar(z, /)
        Convert a complex from rectangular coordinates to polar coordinates.
        
        r is the distance from 0 and phi the phase angle.
    
    rect(r, phi, /)
        Convert from polar coordinates to rectangular coordinates.
    
    sin(z, /)
        Return the sine of z.
    
    sinh(z, /)
        Return the hyperbolic sine of z.
    
    sqrt(z, /)
        Return the square root of z.
    
    tan(z, /)
        Return the tangent of z.
    
    tanh(z, /)
        Return the hyperbolic tangent of z.

DATA
    e = 2.718281828459045
    inf = inf
    infj = infj
    nan = nan
    nanj = nanj
    pi = 3.141592653589793
    tau = 6.283185307179586

FILE
    /usr/share/miniconda/lib/python3.11/lib-dynload/cmath.cpython-311-x86_64-linux-gnu.so

Damit können wir nun die Exponentialfunktion auf eine komplexe Zahl anwenden.

from cmath import exp, pi
exp(0.25j*pi)

(0.7071067811865476+0.7071067811865475j)

Dabei ist das Ergebnis immer eine komplexe Zahl. Daher kann es wünschenswert sein, sowohl das Modul math als auch das Modul cmath zu importieren:

import math, cmath
print(f'reelle Exponentialfunktion:   {math.exp(2)}')
print(f'komplexe Exponentialfunktion: {cmath.exp(0.25j*math.pi)}')

reelle Exponentialfunktion:   7.38905609893065
komplexe Exponentialfunktion: (0.7071067811865476+0.7071067811865475j)

Bei dieser Art des Imports ist durch die Notwendigkeit, das Modul anzugeben, immer klar, um welche Funktion es sich handelt.

Eine andere Möglichkeit wäre ein Umbenennung von einer der beiden Funktionen, wobei der Name nicht zwingend cexp sein müsste..

from math import exp, pi
from cmath import exp as cexp
print(f'reelle Exponentialfunktion:   {exp(2)}')
print(f'komplexe Exponentialfunktion: {cexp(0.25j*math.pi)}')

reelle Exponentialfunktion:   7.38905609893065
komplexe Exponentialfunktion: (0.7071067811865476+0.7071067811865475j)

Frage

Welche Funktion wird verwendet, wenn man nacheinander die Funktion exp() aus dem Modul math und aus dem Modul cmath importiert ohne wie im vorigen Beispiel eine Umbenennung durchzuführen? Probieren Sie es einfach mal aus.

3.5. Variablen und Zuweisungen

Aus der Mathematik kennen wir das Konzept von Variablen, denen man je nach Anwendungsfall bestimmte Werte zuweisen kann. Es ist aber auch möglich, auf die explizite Zuweisung von Werten gänzlich zu verzichten und mit Variablen rein symbolisch zu rechnen. Wir werden im Folgenden immer den ersten Fall im Blick haben, bei dem Variablen ein Wert zugewiesen wird, der sich im Lauf der Programmabarbeitung auch verändern kann. Variablen sind in diesem Sinne Namen für Bereiche im Computerspeicher, die bestimmte Informationen enthalten.

Die Beschränkung auf den ersten Fall bedeutet jedoch nicht, dass es auf Computern nicht möglich wäre, auch rein symbolisch zu rechnen, wie Computeralgebrasysteme zeigen. Auch in Python ist mit Hilfe der sympy-Bibliothek symbolisches Rechnen möglich.

Eine Variable soll nun den Speicherplatz bezeichnen, in dem ein bestimmtes Objekt, also zum Beispiel eine Zahl, eine Zeichenkette oder ein Objekt eines der anderen Datentypen, die wir noch kennenlernen werden, abgespeichert ist. Bedenkt man, dass der Ort im Speicher auch einfach durch eine Zahl angegeben werden könnte, wird klar, dass Variablen eine wichtige Rolle dabei spielen, ein Programm gut lesbar zu machen.

Tipp

Es lohnt sich, bewusst beschreibende Variablennamen zu wählen, auch wenn es etwas Mühe kostet. In den meisten Fällen sind hierfür Variablennamen, die nur aus einem Buchstaben bestehen, ungeeignet, auch wenn sie bequem erscheinen mögen. Denken Sie daran, dass es für andere nicht offensichtlich sein wird, was die Bedeutung einer Variablen x im konkreten Fall ist. Unter Umständen handelt es sich bei dieser anderen Person auch um Sie selbst, wenn Sie nach einem halben Jahr wieder einen Blick auf Ihr Programm werfen. Eine beschreibende Benennung von Variablen ist ein wesentlicher Schritt zu einem gut dokumentierten Programm.

Wie muss ein Variablenname oder allgemein ein Bezeichner aufgebaut sein, damit er als solcher erkannt wird? Die Antwort hängt von der benutzten Programmiersprache ab, so dass wir sie hier konkret für Python beantworten werden. Die wesentlichen Aspekte gelten aber auch für die anderen verbreiteten Programmiersprachen für wissenschaftliche Anwendungen.

In Python besteht ein Bezeichner aus einer beliebigen Zahl von Zeichen, wobei Buchstaben, der Unterstrich (_) und Ziffern zugelassen sind. Das erste Zeichen darf jedoch keine Ziffer sein. Der Unterstrich zu Beginn und am Ende eines Bezeichners impliziert üblicherweise eine spezielle Bedeutung, auf die wir später noch zurückkommen werden. Daher sollte man es sich zur Regel machen, den Unterstrich höchstens innerhalb eines Bezeichners zu verwenden, sofern man nicht bewusst den Unterstrich in anderer Weise einsetzt.

Viel interessanter als Unterstriche sind Buchstaben. Diese umfassen zunächst einmal die Großbuchstaben A-Z und Kleinbuchstaben a-z. Wie sieht es aber mit Umlauten oder gar mit Buchstaben aus anderen Schriftsystemen, beispielsweise griechischen Buchstaben aus? In diesem Zusammenhang stellt sich die Frage, wie Zeichen im Rechner überhaupt in einer binären Form dargestellt werden. Es gibt hierfür zahlreiche Standards, unter anderem den ASCII-Standard, der noch nicht einmal Umlaute kennt, den ISO-8859-1-Standard, der diesen Mangel behebt, aber dennoch im Umfang sehr beschränkt ist, bis hin zum Unicode-Standard, der mehr als hunderttausend Zeichen umfasst. Für den Unicode-Standard gibt es wiederum verschiedene Codierungen, insbesondere die in der westlichen Welt sinnvolle UTF-8-Kodierung. Etwas mehr Details zu diesem Thema sind im Kapitel 12 zu finden.

Weiterführender Hinweis

Ein technisch präzise Beschreibung der erlaubten Zeichen findet sich in der Sprachdokumentation von Python.

Die systematische Unterstützung des Unicode-Standards durch Python impliziert, dass Buchstaben in Bezeichnern alle Zeichen sein können, die im Unicode-Standard als Buchstaben angesehen werden, also neben Umlauten zum Beispiel auch griechische Zeichen. Ob es wirklich sinnvoll ist, Buchstaben von außerhalb des Bereiche A-Z und a-z zu verwenden, sollte man sich im Einzelfall gut überlegen. Man muss sich nur vor Augen halten, was es für Folgen hätte, wenn man ein Programm analysieren müsste, das unter Verwendung von chinesischen Schriftzeichen geschrieben wurde. Auch wenn das folgende Beispiel noch einigermaßen übersichtlich ist, gibt es dennoch einen Eindruck von den Schwierigkeiten, die sich bei einem längeren Skript ergeben könnten.

天堂 = 100
地球 = 10
print(天堂 + 地球)

110

Dennoch ist die Verwendung dieser Schriftzeichen in Python 3 kein Problem, genauso wenig wie die Verwendung von griechischen Buchstaben.

from math import pi as π
Radius = 2
Fläche = π*Radius**2
print(Fläche)

12.566370614359172

Es ist nicht selbstverständlich, dass Variablennamen mit Umlauten, griechischen Buchstaben oder allgemein Zeichen außerhalb der Bereiche A-Z und a-z in anderen Programmiersprachen ebenfalls zugelassen sind. Will man solche Zeichen überhaupt verwenden, so sollte man sich hierüber informieren.

Bei einer Programmiersprache ist auch immer die Frage zu klären, ob zwischen Groß- und Kleinschreibung unterschieden wird. Python tut dies, so dass var, Var und VAR verschiedene Variablen bezeichnen und für Python nichts miteinander zu tun haben. Auch hier stellt sich im Einzelfall die Frage, ob es sinnvoll ist, in einem Programm einen Variablennamen gleichzeitig in Groß- und Kleinschreibung zu verwenden. Es ist jedoch wichtig zu wissen, dass eine Fehlfunktion des Programms ihren Ursprung in einem Tippfehler haben kann, bei dem Groß- und Kleinschreibung nicht beachtet wurden.

Für die Verständlichkeit des Programmcodes ist es angebracht, möglichst aussagekräftige Bezeichner zu verwenden, auch wenn diese im Allgemeinen etwas länger ausfallen. Dabei kann es sinnvoll sein, einen Bezeichner aus mehreren Wörtern zusammenzusetzen. Um die einzelnen Bestandteile erkennen zu können, sind verschiedene Varianten üblich. Man kann zur Trennung einen Unterstrich verwenden, z.B. sortiere_liste. Alternativ kann man neue Worte mit einem Großbuchstaben beginnen, wobei der erste Buchstabe des Bezeichners groß oder klein geschrieben werden kann, z.B. sortiereListe oder SortiereListe. Im ersten Fall spricht man von mixedCase, im zweiten Fall von CamelCase, da die Großbuchstaben an Höcker eines Kamels erinnern. Details zu den in Python empfohlenen Konventionen für Bezeichner finden Sie im Python Enhancement Proposal PEP 8 mit dem Titel »Style Guide for Python Code« im Abschnitt Naming Conventions.

In Python existieren eine Reihe von Schlüsselwörtern, die als Sprachelemente reserviert sind und daher nicht für Bezeichner verwendet werden dürfen. Die aktuelle Liste lässt sich mit einem kleinen Python-Programm erzeugen oder einfach in der Sprachdokumentation von Python nachschlagen. Wichtiger als das kurze Programm, das wir an dieser Stelle noch nicht vollständig verstehen können, ist das Ergebnis der reservierten Schlüsselwörter.

from keyword import kwlist

for nr, kw in enumerate(kwlist):
    print(f'{kw:<16s}', end='')
    if nr % 5 == 4:
        print()

False           None            True            and             as              
assert          async           await           break           class           
continue        def             del             elif            else            
except          finally         for             from            global          
if              import          in              is              lambda          
nonlocal        not             or              pass            raise           
return          try             while           with            yield           

Wichtiger Hinweis

Da griechische Buchstaben in der Physik relativ häufig sind, ist insbesondere darauf zu achten, dass lambda reserviert ist. Der Grund hierfür liegt darin, dass Python so genannte Lambdafunktionen zur Verfügung stellt, die wir im Kapitel 5.6 diskutieren werden.

Variablen kann nun ein Wert zugewiesen werden. Die Zuweisung wird dabei durch ein Gleichheitszeichen gekennzeichnet.

x = 1
print(f'nach der ersten Zuweisung:  x = {x}')
x = x + 1
print(f'nach der zweiten Zuweisung: x = {x}')

nach der ersten Zuweisung:  x = 1
nach der zweiten Zuweisung: x = 2

In der ersten Zeile wird der Variable x der Wert 1 zugewiesen. Die dritte Zeile zeigt deutlich, dass das Gleichheitszeichen nicht im Sinne einer mathematischen Gleichung interpretiert werden darf. Mathematisch hätte diese Gleichung nämlich keine Lösung. In einer Zuweisung wird vielmehr der Code auf der rechten Seite des Gleichheitszeichens ausgewertet. Zu diesem Zeitpunkt hat x noch den Wert 1, so dass sich nach der Addition der Wert 2 ergibt. Dieser Wert wird anschließend der Variablen x zugewiesen, die nun den Wert 2 besitzt. Die Zuweisung ist also eher als x+1 → x zu verstehen.

Sich die zeitliche Abfolge von Zuweisungen klar zu machen, ist zum Beispiel wichtig, wenn man zwei Werte vertauschen möchte. Im folgenden Beispiel weisen wir der Variable x den Wert 1 zu und der Variable y den Wert 2. Wir möchten die beiden Werte nun vertauschen, so dass x den Wert 2 bekommt und y den Wert 1. Das soll unabhängig davon funktionieren, welchen konkreten Wert die beiden Variablen zunächst haben. Man könnte zunächst versucht sein, das Problem auf die folgende Weise zu lösen.

x = 1
y = 2
x = y
y = x
print(x, y)

2 2

Offenbar haben wir auf diese Weise den ursprünglichen Wert von x verloren. Das Problem ist die dritte Zeile, in der wir der Variable x den Wert von y, also 2, zuweisen. Damit wurde der vorherige Wert 1 überschrieben und dieser kann auch in der vierten Zeile nicht auf magische Weise wieder auftreten.

Die Standardlösung für dieses Problem besteht darin, den Wert von x in einer Variablen zwischenzuspeichern.

x = 1
y = 2
tmp = x
x = y
y = tmp
print(x, y)

2 1

Hier wird in der dritten Zeile der Wert von x der Variablen tmp zugewiesen, die wir so genannt haben, weil sie nur temporär zur Zwischenspeicherung benötigt wird. Ihren Wert können wir dann in der fünften Zeile verwenden, um y den ursprünglichen Wert von x zuzuweisen, der in x ja bereits überschrieben wurde.

In Python lässt sich das Problem noch eleganter in folgender Weise lösen.

x = 1
y = 2
x, y = y, x
print(x, y)

2 1

Dies Lösung vermeidet die Einführung einer weiteren Variablen und erfordert auch keine drei Zeile Code, deren Funktion man erst analysieren muss. Vielmehr stellt die dritte Zeile sehr kompakt dar, was passiert. Genau genommen wird hier ein aus zwei Variablen bestehendes Tupel einem anderen Tupel zugewiesen. Dies geschieht parallel, so dass es zu keiner unerwünschten Überschreibung wie zuvor kommen kann. Ein Tupel ist ein zusammengesetzter Datentyp, den wir in Kapitel 6.2 genauer diskutieren werden. Seine Verwendung trägt in unserem Beispiel erheblich dazu bei, den Code gut lesbar zu machen.

In den Zuweisungen haben wir vor und nach dem Gleichheitszeichen jeweils ein Leerzeichen gesetzt. Dies ist nicht zwingend notwendig, verbessert aber die Lesbarkeit des Codes und wird daher auch im bereits weiter oben erwähnten Python Enhancement Proposal PEP 8 empfohlen. Es ist durchaus sinnvoll, sich zumindest an die wesentlichen der in PEP 8 enthaltenen Empfehlungen zu halten, um anderen Personen das Lesen des Codes zu erleichtern.

Eine weitere Empfehlung lautet, eine Zeilenlänge von 79 Zeichen nicht zu überschreiten, auch wenn diese Vorgabe in Zeiten großer Bildschirme nicht mehr ganz so streng gesehen wird Bei überlangen Zeilen kann man mit einem Backslash (\) am Zeilenende eine Fortsetzungszeile erzeugen. In gewissen Fällen erkennt der Python-Interpreter, dass eine Fortsetzungszeile folgen muss, so dass dann der Backslash entfallen kann. Dies ist insbesondere der Fall, wenn in einer Zeile eine Klammer geöffnet wird, die dann erst in einer Folgezeile wieder geschlossen wird.

Es wird häufig empfohlen, den Backslash zur Kennzeichnung einer Fortsetzungszeile zu vermeiden. Stattdessen sollte eine Klammerung verwendet werden, selbst wenn diese ausschließlich zur impliziten Markierung von Fortsetzungszeilen dient. Im folgenden Beispiel wird deutlich, wie man die Klammerung einsetzen kann, auch wenn man die Addition kaum über zwei Zeilen verteilen wird. Im ersten Fall erwartet Python nach dem Pluszeichen den zweiten Summanden, der auf dieser Zeile aber nicht zu finden ist.

4+
5

  Cell In[80], line 1
    4+
      ^
SyntaxError: invalid syntax

Anders ist dies nach einer öffnenden Klammer, da Python dann den Code bis zur zugehörigen schließenden Klammer liest.

(4+
5)

9

3.6. Wahrheitswerte

Im Kapitel 2 hatten wir schon gesehen, dass man den Ablauf eines Programms in Abhängigkeit davon beeinflussen kann, ob eine bestimmte Bedingung erfüllt ist oder nicht. In diesem Zusammenhang spielen Wahrheitswerte oder so genannte boolesche Variable eine Rolle.

Mit einem Wahrheitswert kann die Gültigkeit einer Aussage mit »wahr« oder »falsch« spezifiziert werden. Mögliche Werte in Python sind entsprechend True und False, wobei die Großschreibung des ersten Zeichens wichtig ist. Für die bis jetzt behandelten Datentypen (Integer, Float, Complex) gilt, dass eine Null dem Wert False entspricht, während alle anderen Zahlenwerte einem True entsprechen. Dies lässt sich durch eine explizite Umwandlung mit Hilfe der Funktion bool() überprüfen:

bool(0)

False

bool(42)

True

Wichtige logische Operatoren sind not (Negation), and (logisches Und) und or (logisches Oder). Bei der Negation wird aus True False und umgekehrt.

x = True
not x

False

Nehmen wir noch einen zweiten Wahrheitswert hinzu, so können wir die and-Operation durchführen, die nur dann True ergibt, wenn beide beteiligten Ausdrücke den Wahrheitswert True haben.

y = False
x and y

False

Die or-Operation ergibt True wenn mindestens einer der beiden beteiligten Ausdrücke den Wahrheitswert True hat. Diese Operation muss vom exklusiven Oder unterschieden werden, das nur True ergibt, wenn genau einer der beiden Wahrheitswerte gleich True ist.

x or y

True

Logische Ausdrücke werden in Python von links nach rechts ausgewertet und zwar nur so weit, wie es für die Entscheidung über den Wahrheitswert erforderlich ist. Dies wird in dem folgenden Beispiel illustriert. Im ersten Fall steht das Ergebnis der or-Verknüpfung schon dadurch fest, dass x gleich True ist, so dass die Division durch Null nicht mehr durchgeführt wird.

x = True
y = 0
x or 1/y

True

Anders ist dies bei der and-Verknüpfung. Hier wird die Division ausgeführt mit den bekannten Folgen einer Division durch Null.

x and 1/y

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
Cell In[88], line 1
----> 1 x and 1/y

ZeroDivisionError: division by zero

Wahrheitswerte sind häufig das Ergebnis von Vergleichsoperationen, die in der Tab. 3.2 zusammengestellt sind.

Tab. 3.2 Vergleichsoperationen in Python

Operator	Bedeutung
<	kleiner
<=	kleiner oder gleich
>	größer
>=	größer oder gleich
!=	ungleich
==	gleich

Die folgenden drei Beispiele illustrieren Vergleichsoperationen.

5 != 2

True

5 > 2

True

5 == 2

False

Wichtiger Hinweis

Ein beliebter Fehler besteht darin, beim Test auf Gleichheit nur eines statt zwei Gleichheitszeichen zu verwenden.

In Python kann man Vergleichsoperation auch verketten wie das folgende Beispiel zeigt.

for n in range(10):
    if 2 <= n <= 5:
        print(f'{n} ✓')
    else:
        print(f'{n} ✗')

0 ✗
1 ✗
2 ✓
3 ✓
4 ✓
5 ✓
6 ✗
7 ✗
8 ✗
9 ✗

Hat man es mit Gleitkommazahlen zu tun, so ist ein Test auf Gleichheit meistens nicht sinnvoll, da Rundungsfehler dazu führen können, dass das Ergebnis nicht wie erwartet ausfällt.

x = 3*0.1
y = 0.3
x == y

False

In solchen Fällen ist es besser zu überprüfen, ob die Differenz von zwei Gleitkommazahlen eine vertretbare Schwelle unterschreitet.

eps = 1e-12
abs(x-y) < eps

True

In diesem Zusammenhang kann auch die Funktion isclose() aus dem math-Modul hilfreich sein, das sowohl absolute als auch relative Abweichungen berücksichtigen kann.

import math
help(math.isclose)

Help on built-in function isclose in module math:

isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0)
    Determine whether two floating point numbers are close in value.
    
      rel_tol
        maximum difference for being considered "close", relative to the
        magnitude of the input values
      abs_tol
        maximum difference for being considered "close", regardless of the
        magnitude of the input values
    
    Return True if a is close in value to b, and False otherwise.
    
    For the values to be considered close, the difference between them
    must be smaller than at least one of the tolerances.
    
    -inf, inf and NaN behave similarly to the IEEE 754 Standard.  That
    is, NaN is not close to anything, even itself.  inf and -inf are
    only close to themselves.

3.7. Formatierung von Ausgaben

Wenn man ein Programm ausführt, möchte man in den meisten Fällen eine Ausgabe haben, die im einfachsten Fall auf dem Bildschirm erfolgen kann. In den Codezellen eines Jupyter Notebooks, wie wir sie in diesem Manuskript verwenden, kann man am Ende der Zelle einfach eine Variable oder einen Ausdruck hinschreiben. Dieser wird ausgewertet und das Ergebnis ausgegeben. Dabei handelt es sich zwar um eine bequeme Art der Ausgabe, die aber in Python im Allgemeinen und auch in anderen Programmiersprachen so nicht funktionieren wird.

Stattdessen muss man die print()-Funktion verwenden, die in anderen Programmiersprachen auch einen anderen Namen, beispielsweise write, haben kann. Die print()-Funktion ist uns auch schon in einigen Beispielen begegnet.

Die Ein- und Ausgabe von Daten werden wir erst später im Kapitel 7 genauer diskutieren. Dennoch wollen wir uns schon jetzt mit der Frage beschäftigen, wie man eine Ausgabe in das gewünschte Format bringen kann. Gerade beim Arbeiten mit numerischen Datentypen, die wir zu Beginn dieses Kapitels eingeführt hatten, möchte man unter Umständen in der Lage sein, die Zahl der Nachkommastellen festzulegen oder eine Exponentialschreibweise zu wählen.

Die Möglichkeit, das Format der Ausgabe festzulegen, ist zumindest in allen für das wissenschaftliche Arbeiten relevanten Programmiersprache gegeben. Die Beschreibung des Formats funktioniert typischerweise mit Hilfe eines format strings, der in den verschiedenen Programmiersprachen ähnlich aufgebaut ist, auch wenn es im Detail durchaus Unterschiede geben kann. Wie die auszugebenden Objekte und ihre Formatierung dann im Code anzugeben sind, unterscheidet sich von Programmiersprache zu Programmiersprache. Python selbst stellt hierfür schon mehrere Möglichkeiten zur Verfügung. Wir werden uns auf die Formatierung mit Hilfe von f-Strings beschränken, da sich diese als bevorzugte Methode etabliert hat. Der englische Begriff string ist hier im Sinne einer Zeichenkette zu verstehen.

Wir beginnen mit dem einfachsten Fall einer unformatierten Ausgabe.

x = 1.5
y = 3.14159
print(x**2)
print(x, y)

2.25
1.5 3.14159

Die Zeile 3, die zur ersten Ausgabezeile führt, zeigt, dass in er print()-Funktion nicht nur Variablen angeben kann, sondern auch ganze Ausdrücke, wie hier das Quadrat der Variablen x. Daneben ist es möglich, mehrere Variable gleichzeitig auszugeben. Dazu werden diese im Argument der print()-Funktion durch ein Komma getrennt. Das Leerzeichen nach dem Komma ist für Python nicht relevant, verbessert aber die Lesbarkeit des Codes und ist daher üblich. Auf jeden Fall wird Python in der Ausgabe zwischen den Werten der beiden Variablen immer ein Leerzeichen setzen.

Um die Bedeutung der ausgegebenen Wert anzudeuten, möchte man häufig gerne noch einen Text ausgeben. Im einfachsten Fall kann man diesen Text einfach als weiteres Argument der print()-Funktion in Form einer Zeichenkette angeben. Zeichenketten werden wir erst im Kapitel 6.3 genauer besprechen. Für den Moment ist nur wichtig, dass Zeichenketten durch Anführungszeichen begrenzt werden müssen. Dabei sind sowohl doppelte Anführungszeichen (") als auch einfache Anführungszeichen (') zugelassen, sofern am Anfang und Ende der Zeichenkette das gleiche Zeichen verwendet wird.

print("Näherung für π/3:", y/3)

Näherung für π/3: 1.0471966666666666

Bis jetzt haben wir noch keinerlei Formatierung vorgenommen. Das vorige Beispiel, bei dem die Kreiszahl nur auf fünf Nachkommastellen einging, illustriert aber, dass man beispielsweise die Zahl der Nachkommastellen kontrollieren will. In unserem Beispiel wäre eine Beschränkung auf fünf Nachkommastellen sinnvoll.

print(f"Näherung für π/3: {y/3:.5f}")

Näherung für π/3: 1.04720

Bevor wir das Vorgehen bei der Formatierung in Python systematischer diskutieren, sehen wir uns zunächst das Argument der print()-Funktion in diesem Beispiel genauer an. Durch die Anführungszeichen wird die Zeichenkette begrenzt die ausgegeben wird. Um diese Zeichenkette als f-String zu kennzeichnen, muss ein f vorangestellt werden. Die eigentliche Zeichenkette enthält zum einen einfach Text, wobei wir an dem griechischen Buchstaben sehen, dass wir im Prinzip beliebige Unicodezeichen in UTF-8-Kodierung angeben können.

Daneben enthält die Zeichenkette noch einen Teil, der durch geschweifte Klammern gekennzeichnet ist, und der eine von Python auszuwertenden Ausdruck sowie eine Formatierungsangabe enthält, die durch einen Doppelpunkt voneinander getrennt sind. Der format string lautet hier also .5f und gibt mit Hilfe des Buchstabens f, der für float steht, an, dass eine Gleitkommadarstellung gewünscht wird. Die 5 nach dem Dezimalpunkt legt fest, dass fünf Nachkommastellen auszugeben sind. Wie wir an der Ausgabe im Beispiel sehen, wird die Zahl nicht einfach abgeschnitten, sondern gerundet.

In f-Strings ist die Zahl der auszuwertenden Ausdrücke nicht auf einen beschränkt.

x = 2
power = 0.5
print(f"{x}**{power} = {x**power}")

2**0.5 = 1.4142135623730951

Hier ist zwischen den zwei Sternchen außerhalb der geschweiften Klammern, die direkt so ausgegeben werden, und den Sternchen innerhalb der geschweiften Klammern, die als Exponentierungsoperator fungieren, zu unterscheiden.

Hinweis

Will man im Ausgabetext eine öffnende oder schließende geschweifte Klammer unterbringen, so ist diese zu verdoppeln, also {{ oder }}.

Seit Python 3.8 gibt es eine praktische Möglichkeit, sowohl den Namen als auch den Wert einer Variablen auszugeben.

myvar = 2**0.5
print(f"{myvar = }")
print(f"{myvar =}")
print(f"{myvar= }")
print(f"{myvar=}")

myvar = 1.4142135623730951
myvar =1.4142135623730951
myvar= 1.4142135623730951
myvar=1.4142135623730951

In diesem Beispiel wird deutlich, dass man die Ausgabe von Leerzeichen um das Gleichheitszeichen herum leicht beeinflussen kann. Für ältere Pythonversionen müsste man stattdessen den Variablennamen de facto zweimal angeben.

print(f"myvar = {myvar}")

myvar = 1.4142135623730951

Mit einer Ausnahme haben wir bis jetzt nur Werte von Variablen in einen Text eingebettet, ohne die Form ihrer Ausgabe zu beeinflussen. Dies ist aber beispielsweise bei Gleitkommazahlen wichtig. Wir wollen uns jetzt etwas systematischer mit den Formatierungsmöglichkeiten beschäftigen.

Bei Gleitkommazahlen ist unter anderem die Anzahl der Nachkommastellen von Interesse. Um deutlich zu machen, wie viele Leerzeichen ausgegeben werden, begrenzen wir die Ausgabe mit senkrechten Strichen. In Erweiterung unseres Beispiels weiter oben, in dem wir fünf Nachkommastellen festgelegt hatten, wollen wir nun die ganze Breite der Ausgabe festlegen.

x = 2**0.5
print(f"|{x:6.3f}|")

| 1.414|

Von Interesse für uns ist der Bereich zwischen den geschweiften Klammern, der zunächst den Namen der Variable, also x, enthält und, durch einen Doppelpunkt abgetrennt, die Formatierungsangabe. Die erste Zahl, die auch aus mehr als einer Ziffer bestehen kann, gibt die gesamte Feldbreite an. Diese enthält sowohl Vor- und Nachkommastellen als auch den Dezimalpunkt. Bleibt dann noch Platz, so wird dieser durch Leerzeichen aufgefüllt. Von der gesamten Feldbreite durch einen Punkt abgetrennt wird die Zahl der Nachkommastellen angegeben. In unserem Fall benötigt der Wert von x eine Vorkommastelle und drei Nachkommastellen. Zusammen mit dem Dezimalpunkt macht dies fünf Zeichen, so dass sich noch ein Leerzeichen ergibt. Das abschließend f gibt an, dass der Wert von x als Gleitkommazahl ausgegeben werden soll, also nicht in Exponentialschreibweise.

Wählt man die Feldbreite zu klein, so wird zwar immer noch die gesamte Zahl ausgegeben, aber untereinanderstehende Zahlen werden unter Umständen nicht mehr wie gewünscht zueinander ausgerichtet.

print(f"|{x:4.3f}|")

|1.414|

Dies gilt insbesondere, wenn man die Feldbreiten überhaupt nicht spezifiziert, da dann immer die minimal benötigte Breite belegt wird.

print(f"{x:.3f}")
print(f"{x**7:.3f}")

1.414
11.314

Bei der Ausrichtung von Zahlen ist auch das Vorzeichen relevant. Hierbei kann man angeben, wie bei einer positiven Zahl verfahren wird. Durch Eingabe eines Pluszeichens, eines Leerzeichens oder eines Minuszeichens in der Formatierungsangabe wird für positive Zahlen ein Plus, ein Leerzeichen bzw. gar nichts ausgegeben wie die folgenden Beispiele zeigen.

print(f"|{x:+4.2f}|")
print(f"|{-x:+4.2f}|")
print(f"|{x: 4.2f}|")
print(f"|{-x: 4.2f}|")
print(f"|{x:-4.2f}|")
print(f"|{-x:-4.2f}|")

|+1.41|
|-1.41|
| 1.41|
|-1.41|
|1.41|
|-1.41|

Hier haben wir bewusst die Feldbreite nur auf 4 gesetzt, um den Unterschied zwischen der dritten und fünften Eingabe zu verdeutlichen.

Bei der Ausgabe von Gleitkommazahlen gibt es nun aber das Problem, dass bei sehr kleinen oder sehr großen Zahlen eine feste Anzahl von Nachkommastellen nicht unbedingt geeignet ist.

print(f"{x:10.8f}")
print(f"{x/10e6:10.8f}")
print(f"{x*10e6:10.8f}")

1.41421356
0.00000014
14142135.62373095

Während in der zweiten Zeile die Zahl der ausgegebenen signifikanten Stellen dramatisch reduziert ist, ist sie in der dritten Zeile unter Umständen unerwünscht groß. In solchen Fällen bietet es sich an, eine Ausgabe in Exponentialdarstellung zu verlangen, die man mit Hilfe des Buchstabens e an Stelle des bisherigen f erhält.

print(f"|{x:10.8e}|")
print(f"|{x:10.4e}|")
print(f"|{x/10e6:14.8e}|")
print(f"|{x:20.8e}|")

|1.41421356e+00|
|1.4142e+00|
|1.41421356e-07|
|      1.41421356e+00|

Die erste Eingabe zeigt, wie man eine Exponentialdarstellung mit 8 Nachkommastellen erhält. Der Exponent wird mit ausgegeben, obwohl er nur für \(10^0=1\) steht. Die Zahl der Nachkommastellen lässt sich, wie erwartet und wie in der zweiten Eingabe zu sehen ist, bei Bedarf anpassen. In diesem Beispiel wird die Feldbreite von 10 gerade ausgenutzt. Das dritte Beispiel zeigt, dass wir nun auch bei der Ausgabe von kleinen Zahlen keine signifikanten Stellen verlieren. Auch für große Zahlen ändert sich die Zahl der signifikanten Stellen nicht. Macht man wie in der vierten Zeile die Feldlänge größer, so wird entsprechend viel Leerplatz auf der linken Seite ausgegeben.

Weiterführender Hinweis

Um etwas über die Möglichkeiten der Positionierung der Ausgabe zu erfahren, können Sie im letzten Beispiel folgende Formatspezifikationen ausprobieren: {:<20.8e}, {:=+20.8e} und {:^20.8e}.

Häufig möchte man die Exponentialschreibweise nur verwenden, wenn die auszugebende Zahl hinreichend groß oder klein ist. Ein solches Verhalten erreicht man durch Angabe des Buchstabens g.

print(f"|{x/10e4:15.8g}|")
print(f"|{x/10e3:15.8g}|")
print(f"|{x*10e6:15.8g}|")
print(f"|{x*10e7:15.8g}|")

|  1.4142136e-05|
|  0.00014142136|
|       14142136|
|  1.4142136e+08|

Hier wird durch den Wechsel der Darstellung insbesondere sichergestellt, dass immer die gleiche Anzahl von signifikanten Stellen ausgegeben wird. Die genaue Regel für die Umstellung der Darstellungsart kann man in der Dokumentation der Python-Standardbibliothek unter dem Thema Format Specification Mini-Language nachlesen, die auch alle weiteren Aspekte der Formatierung detailliert beschreibt.

Betrachten wir nun noch die Formatierung von Integers.

n = 42
print(f"|{n}|{n:5}|{n:05}|")

|42|   42|00042|

Integers in Dezimaldarstellung benötigen keinen Buchstaben zur Formatspezifikation. Man kann aber ein d für Dezimaldarstellung angeben. Ähnlich wie bei den Gleitkommazahlen lässt sich die Feldbreite festlegen. Gibt man vor der Feldbreite eine Null an, so wird das Feld vor der auszugebenden Zahl mit Nullen aufgefüllt. Dies kann zum Beispiel bei der Ausgabe in anderen Zahlensystemen interessant sein. Python unterstützt insbesondere die Ausgabe im Binärformat (b), Oktalformat (o) und im Hexadezimalformat (x).

print(f"|{n:}|{n:8b}|{n:8o}|{n:8x}|{n:08b}|")

|42|  101010|      52|      2a|00101010|

Frage

Was ändert sich, wenn man b, o und x durch die entsprechenden Großbuchstaben ersetzt? Welche Auswirkungen hat ein #, das vor der Feldbreite inklusive einer eventuell vorhandenen Null steht?

Abschließend sei noch angemerkt, dass die print()-Funktion standardmäßig einen Zeilenumbruch an das Ende des auszugebenden Textes anhängt. Dies ist jedoch nicht immer gewünscht und lässt sich mit Hilfe der Option end beeinflussen. Folgendes Beispiel zeigt die Funktionsweise.

print("x", end="..")
print("x", end="")
print("x")

x..xx

Aufgrund der ersten Zeile werden zwei Punkte an das x angehängt, ohne einen Zeilenumbruch zu verursachen. Letzteres wird auch in der zweiten Zeile vermieden. Es werden wegen der leeren Zeichenkette ("") aber keine weiteren Zeichen an das zweite x angehängt. In der dritten Zeile schließlich wird ein weiteres x angehängt. Zusätzlich wird ein Zeilenumbruch erzeugt, da das Argument end nicht gesetzt wurde.