Kontrollstrukturen

Inhalt

4. Kontrollstrukturen#

Im Kapitel 2 hatten wir bereits kurz die Möglichkeit angesprochen, den Ablauf eines Programms zu beeinflussen, sei es dadurch, dass ein Programmteil in einer Schleife mehrfach ausgeführt wird oder dass ein Programmteil nur dann ausgeführt wird, wenn eine gewisse Bedingung erfüllt ist. Solche Kontrollstrukturen sind essentiell, um die Abarbeitung eines Programms zu steuern. Wir werden in diesem Kapitel zwei Arten von Schleifen betrachten, die for-Schleife und die while-Schleife, bei denen auf verschiedene Weise die Zahl der Schleifendurchläufe kontrolliert wird. Anschließend werden wir uns mit Verzweigungen der Form if … else beschäftigen und auch komplexere Verzweigungen kennenlernen. Diese Programmkonstrukte finden sich in allen für das wissenschaftliche Rechnen relevanten Programmiersprachen, auch wenn die konkrete syntaktische Umsetzung unterschiedlich sein kann.

Wir hatten im vorigen Kapitel bereits gesehen, dass im Fehlerfall, zum Beispiel bei der Division durch null, Ausnahmen oder exceptions auftreten. Diese müssen nicht zwingend zum Abbruch des Programms führen, sondern sie können geeignet behandelt werden. Diesen Aspekt der Steuerung des Programmablaufs werden wir im letzten Abschnitt dieses Kapitels kennenlernen.

4.1. For-Schleife#

Sollen bestimmte Anweisungen mehrfach ausgeführt werden, wobei die Anzahl der Wiederholungen zuvor bestimmt werden kann, bietet sich die Verwendung einer for-Schleife an. Gegenüber der expliziten Wiederholung von Befehlen ergeben sich eine Reihe von Vorteilen. Zunächst einmal spart man sich Tipparbeit und verbessert erheblich die Lesbarkeit des Programms. Zudem ist eine explizite Wiederholung nur möglich, wenn die Zahl der Wiederholungen bereits beim Schreiben des Programms feststeht und nicht erst beim Ausführen des Programms berechnet wird.

Wir verdeutlichen das anhand eines Beispiels, in dem wir einige Quadratzahlen berechnen. In einer for-Schleife würde das für die Zahlen von 0 bis 4 folgendermaßen gehen.

for n in range(5):
    print(f"{n:4} {n**2:4}")

Verzichtet man auf die Schleife, so wäre der folgende Code erforderlich.

print(f"{0:4} {0**2:4}")
print(f"{1:4} {1**2:4}")
print(f"{2:4} {2**2:4}")
print(f"{3:4} {3**2:4}")
print(f"{4:4} {4**2:4}")

Es dürfte offensichtlich sein, dass die erste Variante zu bevorzugen ist. Dies gilt insbesondere, wenn die Zahl der Durchläufe variabel sein soll, wie im folgenden Fall.

nmax = 7
for n in range(nmax):
    print(f"{n:4} {n**2:4}")

Sehen wir uns den Aufbau der for-Schleife genauer an. Das Schlüsselwort for kennzeichnet den Beginn einer Schleife. Dann folgt der Name der Variable, in unserem Fall also n, die bei der Abarbeitung der Schleife vorgegebene Werte annimmt, und im Rahmen der Schleife verwendet werden kann. Im Allgemeinen können hier auch mehrere Variablennamen vorkommen, wie wir später im Kapitel 6 sehen werden. Die Werte, die die Variable n in unserem Beispiel annehmen kann, werden durch die range-Anweisung bestimmt. Zwar werden die Werte erst bei Bedarf generiert, aber wir können sie uns ansehen, indem wir explizit eine Liste der Werte erzeugen lassen.

list(range(5))

[0, 1, 2, 3, 4]

Es wird also eine Liste von aufeinanderfolgenden ganzen Zahlen erzeugt, die hier fünf Elemente enthält. Zu beachten ist, dass die Liste mit null beginnt und nicht mit Eins. Wir werden uns diesen zusammengesetzten Datentyp im Kapitel 6.1 noch genauer ansehen. Für den Moment genügt jedoch die intuitive Vorstellung von einer Liste. In der ersten Zeile der for-Schleife, die mit einem Doppelpunkt enden muss, wird also festgelegt, welchen Wert die Schleifenvariable n bei den aufeinanderfolgenden Schleifendurchläufen jeweils annimmt.

Mehr Flexibilität in der range()-Funktion

Mit nur einem Argument erzeugt die range()-Funktion wie oben gesehen ganze Zahlen von 0 bis ausschließlich dem angegebenen Wert. Gibt man zwei Argumente an, so entsprechen diese dem Startwert und dem Wert, der gerade nicht mehr angenommen wird. Gibt man ein drittes Argument an, so entspricht dieses der Schrittweite, die übrigens auch negativ sein kann. Alle Argumente müssen aber ganze Zahlen sein. Spielen Sie einfach mal ein bisschen mit der range()-Funktion herum.

Der Codeteil, der im Rahmen der Schleife im Allgemeinen mehrfach ausgeführt wird und im obigen Beispiel nur aus einer Zeile besteht, ist daran zu erkennen, dass er eingerückt ist. Zur Verdeutlichung vergleichen wir zwei Beispiele, die sich lediglich in der Einrückung der letzten Zeile unterscheiden. Im ersten Beispiel ist die letzte Zeile Bestandteil der Schleife und wird demnach zweimal ausgeführt.

for n in range(2):
    print(f"Schleifendurchlauf {n+1}")
    print("Das war's.")

Schleifendurchlauf 1
Das war's.
Schleifendurchlauf 2
Das war's.

Rückt man die letzte Zeile dagegen aus, so wird sie erst ausgeführt nachdem die Schleife zweimal durchlaufen wurde.

for n in range(2):
    print(f"Schleifendurchlauf {n+1}")
print("Das war's.")

Schleifendurchlauf 1
Schleifendurchlauf 2
Das war's.

Im vorliegenden Beispiel ist sicher die zweite Variante adäquat.

Entscheidend für die Zugehörigkeit zur Schleife ist also die Einrückung, wobei die Zahl der Leerstellen im Prinzip frei gewählt werden kann, aber innerhalb des ganzen Schleifenkörpers konstant sein muss. Ein guter Kompromiss zwischen kaum sichtbaren Einrückungen und zu großen Einrückungen, die bei geschachtelten Schleifen schnell zu Platzproblemen führen, ist eine Einrückung von vier Leerzeichen. So wird dies auch im PEP 8 empfohlen, dem Python Enhancement Proposal, das Empfehlungen zur Formatierung von in Python geschriebenem Programmcode gibt. Diese Empfehlungen sind zwar nicht verpflichtend, aber die wichtigsten Hinweise werden von den meisten Programmierern respektiert.

Weiterführender Hinweis

Im PEP 8 wird auch eine maximale Zeilenlänge von 79 Zeichen empfohlen. Sehr lange Zeilen sind unter Umständen schwer zu lesen und führen bei kleineren Bildschirmen zu Problemen mit Zeilenumbrüchen. Da heutzutage oft größere Monitore zum Einsatz kommen, geben manche Projekte eine Maximallänge von 99 Zeichen vor.

Da die Verwendung der Einrückung als syntaktisches Merkmal ungewöhnlich ist, wollen wir kurz zwei Beispiele aus anderen Programmiersprachen besprechen. In FORTRAN 90 könnte eine Schleife folgendermaßen aussehen:

PROGRAM Quadrat
DO n = 0, 4
   PRINT '(2I4)', n, n**2
END DO
END PROGRAM Quadrat

Hier wurde nur aus Gründen der Lesbarkeit eine Einrückung vorgenommen. Relevant für das Ende der Schleife ist lediglich das abschließende END DO. Während man sich hier selbst dazu zwingen muss, gut lesbaren Code zu schreiben, zwingt Python den Programmierer durch seine Syntax dazu, übersichtlichen Code zu produzieren.

Auch im folgenden C-Code sind die Einrückungen nur der Lesbarkeit wegen vorgenommen worden. Der Inhalt der Schleife wird durch die öffnende geschweifte Klammer in Zeile 6 und die schließende geschweifte Klammer in Zeile 9 definiert.

#include <stdio.h>

void main(){
   int i;
   int quadrat;
   for(i = 0; i < 5; i++){
         quadrat = i*i;
         printf("%4i %4i\n", i, quadrat);
   }
}

Würde man auf die Klammern verzichten, so wäre nur die der for-Anweisung folgende Zeile, also Zeile 7, Bestandteil der Schleife. Dagegen befände sich Zeile 8 trotz der Einrückung nicht mehr im Schleifenkörper.

Schleifen werden in Python häufig anders organisiert als dies in Sprachen wie Fortran und C der Fall ist. Diesen Unterschied können wir durch zwei Realisierungen der gleichen Problemstellung illustrieren. Im Kapitel 2 hatten wir eine Implementation des Schere-Papier-Stein-Spiels in Python besprochen. Darin kam unter anderem eine Liste der drei beteiligten Gegenstände vor. An dieser Stelle ist nur wichtig, dass wir Elemente einer Liste durch einen Index adressieren können, so wie wir das für die Komponenten eines Vektors in der Mathematik gewohnt sind.

Stellen wir uns nun vor, dass wir eine Liste der drei Gegenstände ausgeben wollen. Eine erste Variante besteht darin, mit Hilfe der range()-Funktion eine Schleife über die Indizes zu programmieren, in der dann die Elemente der Liste adressiert und ausgegeben werden.

objekte = ['Stein', 'Papier', 'Schere']
for idx in range(3):
    print(objekte[idx])

Stein
Papier
Schere

Eine solche Vorgehensweise ist für Sprachen wie Fortran und C typisch. Da der Index in gleichmäßigen Schritten hochgezählt wird, ist es für den Computer möglich, effizient auf die einzelnen Listenobjekte zuzugreifen. Dies gilt insbesondere, wenn es sich bei den Listenobjekten um Zahlen handelt, die alle gleich viel Speicher in Anspruch nehmen. Diese erste Variante wird in Python eigentlich nur in besonderen Fällen verwendet, in denen die Rechengeschwindigkeit im Vordergrund steht.

In Python üblicher ist die zweite Variante, bei der direkt über die Liste iteriert wird.

for objekt in ['Stein', 'Papier', 'Schere']:
    print(objekt)

Stein
Papier
Schere

Aus der zweiten Zeile wird hier offensichtlich, dass die Schleife über alle Elemente der Liste geht. Der Code ist insgesamt etwas leichter zu lesen und schneller zu schreiben als der Code der ersten Variante und wird daher normalerweise von Python-Programmierern bevorzugt.

Wir betrachten noch ein zweites Beispiel, das von seiner Struktur gerade beim numerischen Arbeiten typisch ist. Dabei wollen wir die Kreiszahl π mit Hilfe der Summendarstellung

\[\sum_{n=1}^\infty\frac{1}{n^2} = \frac{\pi^2}{6}\]

bestimmen. Dies geht allein schon deshalb nur näherungsweise, weil wir die Summe bei einem wählbaren maximalen Index abschneiden müssen. Dabei fällt der Fehler invers linear mit diesem maximalen Index. Betrachten wir nun den zugehörigen Python-Code.

from math import sqrt

nmax = 100000
summe = 0
for n in range(nmax):
    summe = summe + 1/(n+1)**2
print(sqrt(6*summe))

3.141583104326456

Den maximalen Summationsindex hätten wir hier auch direkt in das Argument der range()-Funktion schreiben können. Wollen wir diesen Wert aber ändern, so ist die betreffende Stelle leichter zu finden, da der Variablenname nmax auf die Bedeutung dieses Wert hinweist.

Zwei Aspekte wollen wir an diesem Beispiel betonen. Zum einen übersieht man leicht, dass im Nenner nicht einfach n**2 stehen darf. Dies würde zu einer Division durch null führen, da der erste Wert, der von der range()-Funktion geliefert wird, gerade null ist. Da die Summation bei 1 beginnt, müssen wir also im Nenner (n+1)**2 schreiben.

Ein zweiter Aspekt wird gerne übersehen. Im Schleifenkörper, der hier nur aus der vorletzten Zeile besteht, wird wie bei jeder Zuweisung zunächst die rechte Seite ausgewertet. Dabei erwartet der Pythoninterpreter schon beim ersten Durchlauf, dass die Variable summe einen Wert besitzt. Auch wenn wir einen fehlenden Wert intuitiv einfach auf null setzen würden, ist es für Python ein großer Unterschied, ob eine Variable den Wert null hat oder überhaupt keinen Wert besitzt. Dies bedeutet, dass unser Beispiel nicht mehr läuft, wenn wir die vierte Zeile weglassen. Aus technischen Gründen entfernen wir die Variable hier explizit, da sie sonst ihren Wert aus der obigen Zelle behält.

del summe

Unser neuer Code hat nun die folgende Form.

from math import sqrt

nmax = 100000
for n in range(nmax):
    summe = summe + 1/(n+1)**2
print(sqrt(6*summe))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[11], line 5
      3 nmax = 100000
      4 for n in range(nmax):
----> 5     summe = summe + 1/(n+1)**2
      6 print(sqrt(6*summe))

NameError: name 'summe' is not defined

Wie erwartet schlägt die Ausführung fehl, weil die Variable summe beim allerersten Schleifendurchlauf noch nicht definiert ist. Es ist also unbedingt erforderlich, die Variable vor der Schleife zu definieren. Man spricht hier auch von einer Initialisierung.

for-Schleifen können auch geschachtelt werden. Wir zeigen dies an einem Beispiel, das die Wahrheitswerttabelle für die logische UND-Verknüpfung (&) und die logische ODER-Verknüpfung (|) darstellt.

print("  arg1   arg2   arg1 & arg2   arg1 | arg2 ")
print("------------------------------------------")
for arg1 in [False, True]:
    for arg2 in [False, True]:
        print(f" {arg1!s:5}  {arg2!s:5}   {arg1&arg2!s:^11}   {arg1|arg2!s:^11}")

  arg1   arg2   arg1 & arg2   arg1 | arg2 
------------------------------------------
 False  False      False         False   
 False  True       False         True    
 True   False      False         True    
 True   True       True          True    

Weiterführender Hinweis

Unter anderem für solche Situationen stellt in Python das itertools-Modul der Standardbibliothek hilfreiche Funktionen zur Verfügung.

Wie man in den ersten beiden Spalten der Ausgabe sieht, wird zunächst in der äußeren Schleife arg1 auf False gesetzt. Anschließend wird die innere Schleife abgearbeitet, in der arg2 nacheinander die Werte False und True annimmt. Erst dann wird in der äußeren Schleife arg1 auf True gesetzt und danach wiederum die innere Schleife abgearbeitet.

Gerade in einer doppelten Schleife ist die Einrückung wichtig, die darüber bestimmt, in welcher Schleife eine Befehlszeile abgearbeitet wird. Da die print-Anweisung relativ zur inneren Schleife eingerückt ist, wird sie in dieser ausgeführt. und entsprechend werden zusätzlich zum Tabellenkopf vier Zeile ausgegeben. Würde man die letzte Zeile nur vier Leerzeichen weit einrücken, würde sie in die äußere Schleife wandern und nur zweimal ausgeführt werden.

Versucht man dies, gibt es zunächst allerdings ein Problem.

print("  arg1   arg2   arg1 & arg2   arg1 | arg2 ")
print("------------------------------------------")
for arg1 in [False, True]:
    for arg2 in [False, True]:
    print(f" {arg1!s:5}  {arg2!s:5}   {arg1&arg2!s:^11}   {arg1|arg2!s:^11}")

  Cell In[13], line 5
    print(f" {arg1!s:5}  {arg2!s:5}   {arg1&arg2!s:^11}   {arg1|arg2!s:^11}")
    ^
IndentationError: expected an indented block after 'for' statement on line 4

Jede Schleife erwartet nämlich einen eingerückten Block von mindestens einer Zeile Länge. In unserem Fall ist es eigentlich nicht sinnvoll, die innere Schleife leer zu lassen. Gerade bei der Programmentwicklung kann es aber vorkommen, dass man eine Schleife schon mal anlegen, aber erst später mit Code füllen will. Häufiger kommt dies bei Funktionen vor, in denen sich das gleiche Problem stellt. Dann hilft der Befehl pass weiter, der Python signalisiert, dass es hier nichts zu tun gibt.

print("  arg1   arg2   arg1 & arg2   arg1 | arg2 ")
print("------------------------------------------")
for arg1 in [False, True]:
    for arg2 in [False, True]:
        pass
    print(f" {arg1!s:5}  {arg2!s:5}   {arg1&arg2!s:^11}   {arg1|arg2!s:^11}")

  arg1   arg2   arg1 & arg2   arg1 | arg2 
------------------------------------------
 False  True       False         True    
 True   True       True          True    

Jetzt wird die print-Anweisung tatsächlich nur zweimal ausgeführt, nämlich jeweils am Ende der Abarbeitung der äußeren Schleifendurchläufe. Außerdem kann man hier noch feststellen, dass die Laufvariable arg2 der inneren Schleife auch nach der Abarbeitung der Schleife zur Verfügung steht. Sie hat dabei den Wert, der ihr zuletzt zugewiesen wurde, in unserem Fall also True.

4.2. While-Schleife#

Bei der gerade besprochenen for-Schleife kennt man im Vorhinein die Zahl der Durchläufe. Dies ist jedoch nicht immer der Fall. Gelegentlich möchte man eine Schleife ausführen, so lange eine bestimmte Bedingung erfüllt ist. Einen eher untypischen Fall hatten wir in Kapitel 2 kennengelernt. Dort war die Bedingung immer wahr, so dass die Schleife, zumindest im Prinzip, unendlich lange laufen konnte. In unserem Beispiel wollen wir dagegen eine Bedingung stellen, die entweder wahr oder falsch sein kann.

Konkret wollen wir uns vorstellen, dass wir mit einem Würfel so lange würfeln bis wir eine Sechs erhalten. Wir wollen uns fragen, wie lange es im Mittel dauert, bis wir eine Sechs gewürfelt haben und welche Wurfanzahl die häufigste ist. Diese Fragen lassen sich mathematisch streng beantworten, aber wir wollen nun den Computer heranziehen.

from random import randrange
import matplotlib.pyplot as plt

def wait_for_six():
    result = randrange(1, 7)
    ncasts = 1
    while result != 6:
        result = randrange(1, 7)
        ncasts = ncasts + 1
    return ncasts

waiting_sequence = [wait_for_six() for n in range(100000)]
plt.hist(waiting_sequence, bins=30, range=(1, 30), density=True)
plt.show()

_images/f4d1cf367ca60b13c30ef17fbee1a5d99bc499960cd787bd36d7d06919fd5b31.png

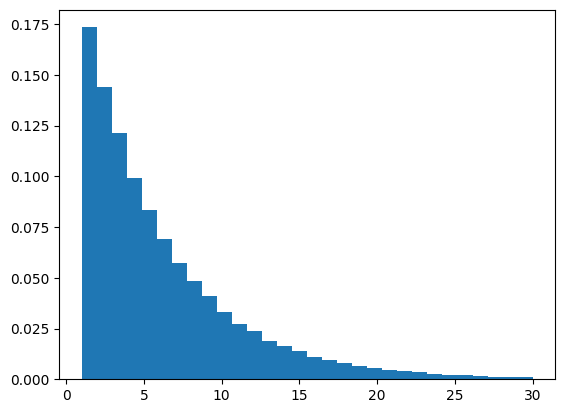
Das Histogramm gibt die Wahrscheinlichkeit an, dass eine 6 zum ersten Mal nach der entsprechenden Anzahl von Versuchen gewürfelt wird.

Bei der Besprechung des Codes wollen wir uns auf die Funktion wait_for_six() konzentrieren, die die while-Schleife enthält und für eine zufällige Realisierung von Würfen bestimmt, wie viele Würfe benötigt werden, um zum ersten Mal eine Sechs zu erhalten. Der Code setzt das Vorgehen beim Würfeln in direkter, wenn auch nicht unbedingt optimaler Weise um. Zunächst wird unter Verwendung der Zufallsfunktion randrange eine Zahl zwischen 1 und 6 gewürfelt. Gleichzeitig wird der Zähler ncasts, der die Anzahl der Würfe angibt, entsprechend auf eins gestellt. Wurde keine 6 gewürfelt, ist also die Bedingung result != 6 erfüllt, so wird die while-Schleife durchlaufen, wobei wieder gewürfelt und der Zähler ncasts um eins erhöht wird. Die while-Schleife wird erst verlassen, wenn eine 6 gewürfelt wurde, da dann die Bedingung result != 6 nicht erfüllt ist. Abschließend gibt die Funktion wait_for_six die Zahl der Würfe zurück.

Die grundsätzliche Struktur des Codes entspricht derjenigen, die wir von der for-Schleife bereits kennen. Vor der Schleife findet hier eine Initialisierung statt, der wir schon bei dem Summationsbeispiel im vorigen Abschnitt begegnet sind. Die erste Zeile der eigentlichen while-Schleife beginnt mit dem Schlüsselwort while anstelle des Schlüsselworts for. In beiden Fällen endet die Zeile mit einem Doppelpunkt. Bei der while-Schleife ist außerdem eine Bedingung, hier result != 6, anzugeben. Nur wenn diese Bedingung erfüllt ist, wird der eingerückte Block ausgeführt und anschließend wieder die Bedingung überprüft. Andernfalls wird die Ausführung des Programms nach dem eingerückten Block fortgesetzt.

Aufmerksamen Leserinnen und Lesern fällt in diesem Code vielleicht auf, dass der Code für das Würfeln wiederholt wird. Am Ende von Kapitel 2 hatten wir darauf angewiesen, dass in solchen Fällen die Gefahr von Programmierfehlern droht. Dies könnte beispielsweise der Fall sein, wenn man statt für einen normalen Würfel das Programm auf einen der in Abb. 4.1 gezeigten Würfel mit 12 oder 20 Flächen übertragen möchte. Dann kann es passieren, dass man aus Versehen nur einen der beiden Aufrufe der randrange()-Funktion korrigiert, womit das Programm fehlerhaft wäre.

_images/wuerfel.png — Abb. 4.1 Dodekaeder- und Ikosaederwürfel.#

Im Prinzip ließe sich unser Problem eleganter lösen, wenn man die Bedingung nicht zu Beginn der while-Schleife überprüfen würde, sondern an deren Ende. Dann würde die Schleife auf jeden Fall einmal durchlaufen werden. Es würde also auf jeden Fall einmal gewürfelt werden und wir würden nur eine Zeile mit einem Aufruf von randrange benötigen. In Python ist dies nicht direkt möglich, aber wir werden weiter unten auf alternative Lösungen zu sprechen kommen. In anderen Sprachen gibt es dagegen ein do … while, wie zum Beispiel in C, oder ein repeat … until wie in Pascal. Dabei wird am Ende getestet.

Ein einfaches Beispiel, das im Prinzip eine absteigende Folge von Quadratzahlen ausgibt, ist hier in C realisiert.

#include <stdio.h>

void main(){
   int i=-1;
   do {printf("%4i %4i\n", i, i*i);
       i = i-1;
   } while (i>0);
}

Nach der Kompilation des Codes kann man das Programm ausführen und erhält als Ausgabe

  -1    1

In Zeile 4 wird der Wert von i auf -1 gesetzt. Würde die Bedingung i>0 schon zu Beginn der Schleife ausgewertet werden, würde man keine Ausgabe erhalten. Im vorliegenden Code erfolgt die Überprüfung aber am Ende, so dass die Schleife für den Wert -1 für i durchlaufen wird. Anschließend hat i den Wert -2 und die Schleife wird beendet. Hier sei nochmals angemerkt, dass die Einrückungen in C nicht erforderlich sind, sondern dass stattdessen die geschweiften Klammerpaare relevant sind.

Entsprechend funktioniert das repeat … until-Konstrukt in Pascal.

program Quadrat;
var
  i: integer;
begin
  i := -1;

  repeat
    writeln(i, '   ', i*i);
    i := i-1;
  until i <= 0;

end.

Einen Unterschied gibt es im Verhalten, wenn die angegebene Bedingung erfüllt ist. Im C-Beispiel wird die Schleife dann fortgesetzt, während sie im Pascal-Beispiel beendet wird. Entsprechend sind die beiden Bedingungen verschieden formuliert.

Wie können wir nun unsere anfängliche Lösung so verbessern, dass der Aufruf von randrange in der Funktion wait_for_six nur einmal statt zweimal vorkommt? Eine Möglichkeit besteht darin, den Aufruf in die Bedingung zu verschieben.

from random import randrange

def wait_for_six():
    ncasts = 1
    while randrange(1, 7) != 6:
        ncasts = ncasts + 1
    return ncasts

waiting_sequence = [wait_for_six() for n in range(100000)]
average = sum(waiting_sequence)/len(waiting_sequence)
print(average)

6.00876

Hier wird zu Beginn der Anfangswert des Zählers ncasts schon im Vorgriff auf das anschließende Würfeln auf eins gesetzt. Auch die letzten beiden Zeilen wurden geändert, was aber nichts mit dem Code in der Funktion wait_for_sixzu tun hat. Diese Änderung soll lediglich dafür sorgen, dass statt einem Histogramm der Mittelwert der Würfe ausgegeben wird. Da das angezeigte Ergebnis auf einer endlichen Anzahl von Veruschen beruht, weicht es ein wenig vom analytischen Ergebnis, nämlich 6, ab.

Ein Nachteil dieser Lösung besteht darin, dass man das Ergebnis des Wurfes nicht ausgeben kann, da es keiner Variable zugewiesen wird. Seit Python 3.8 lässt sich dieses Problem mit dem sogenannten Walroß-Operator := lösen, dessen Name sich auf die Augen und Stoßzähne eines Walrosses bezieht. Der Code könnte dann folgendermaßen aussehen.

from random import randrange

def wait_for_six():
    ncasts = 1
    while (result := randrange(1, 7)) != 6:
        print(result)
        ncasts = ncasts + 1
    print(result)
    return ncasts

wait_for_six()

Eine do … while- oder repeat … until-Konstruktion, bei der Bedingung tatsächlich erst am Ende abgeprüft wird, lässt sich in Python mit einer Endlosschleife realisieren.

from random import randrange

def wait_for_six():
    ncasts = 0
    while 1:
        result = randrange(1, 7)
        ncasts = ncasts + 1
        if result == 6:
            break
    return ncasts

waiting_sequence = [wait_for_six() for n in range(100000)]
average = sum(waiting_sequence)/len(waiting_sequence)
print(average)

5.98405

Hier macht man sich zunutze, dass eine Schleife mit der break-Anweisung verlassen werden kann. Zu beachten ist dabei, dass die Bedingung angepasst werden muss, da das Verlassen erfolgen soll, falls eine 6 gewürfelt wurde.

Abschließend sei betont, dass der Programmierer bei der Verwendung von while-Schleifen und ähnlichen Konstrukten selbst dafür verantwortlich ist sicherzustellen, dass die Schleife irgendwann beendet wird. Andernfalls liegt eine Endlosschleife vor und das Programm muss von außen abgebrochen werden. Eine Endlosschleife hat dabei nicht immer die mehr oder wenige offensichtliche Form wie im obigen Code mit while 1 oder while True. Vergisst man zum Beispiel, eine für die Bedingung relevante Variable zu aktualisieren, so kann es sein, dass die while-Schleife nie zu einem Ende kommt. Ein sehr simples Beispiel zeigt das folgende Codestück.

n = 0
while n < 10:
    print(n, n**2)

Hier wurde vergessen, den Zähler n in der Schleife adäquat zu verändern.

4.3. Verzweigungen#

Eine andere Art von Kontrollstruktur, die nicht die Wiederholung von Programmcode regelt, sondern vielmehr auf der Basis einer gegebenen Bedingung entscheidet, welcher Code ausgeführt wird, sind Verzweigungen.

Im einfachsten Fall wird zusätzlicher Code ausgeführt, wenn eine Bedingung erfüllt ist. Diese Kontrollstruktur basiert auf der if-Anweisung. Zur Illustration greifen wir auf die näherungsweise Berechnung der Kreiszahl zurück, die wir im Kapitel 4.1 betrachtet hatten. Insbesondere wenn die Rechnung insgesamt länger dauert, möchte man vielleicht die Konvergenz der Summation bereits während des Programmlaufs beurteilen. So können wir uns zum Beispiel jeweils das Zwischenergebnis nach zehntausend Iterationen ausgeben lassen.

from math import sqrt

nmax = 100000
summe = 0
for n in range(nmax):
    summe = summe + 1/(n+1)**2
    if n % 10000 == 0:
        print(f"{n:10}  {summe:18.16f}")
print(sqrt(6*summe))

         0  1.0000000000000000
1.6448340818460654
1.6448840705979586
1.6449007351814806
1.6449090677856950
1.6449140674482257
1.6449174005982372
1.6449197814400827
1.6449215670826174
1.6449229559223180
141583104326456

Hier wird in der if-Anweisung überprüft, ob der Schleifenzähler ohne Rest durch Zehntausend teilbar ist. Dann ist der Wahrheitswert des logischen Ausdrucks gleich True und der folgende Code-Block wird ausgeführt. Andernfalls wird dieser Block einfach übersprungen. Wie wir es schon von den for- und while-Schleifen kennen, ist der Code-Block, der zur if-Anweisung gehört, durch die Einrückung kenntlich gemacht. Die print-Anweisung in der letzten Zeile ist nicht mehr eingerückt und gehört damit weder zur if-Anweisung noch zur for-Schleife. Sie wir also erst am Ende des Programmlaufs genau einmal ausgeführt.

Besteht der Code-Block einer if-Anweisung nur aus einer einzigen Zeile, so kann man den gesamten Code in einer einzigen Zeile schreiben. Dies ist allerdings nur sinnvoll, wenn die Anweisung im Code-Block relativ kurz ist. Statt

x = -4
if x < 0:
    x = -x
print(f'{x = } ist bestimmt nicht negativ.')

x = 4 ist bestimmt nicht negativ.

kann man also auch

x = -4
if x < 0: x = -x
print(f'{x = } ist bestimmt nicht negativ.')

x = 4 ist bestimmt nicht negativ.

schreiben. Meistens wird aber die erste Variante übersichtlicher sein.

Bei komplizierteren logischen Ausdrücken kann es auch sinnvoll sein, einen Variablennamen einzuführen, um die Bedeutung des Ausdrucks zu verdeutlichen. Wir illustrieren das anhand eines kleinen Programms, das eine Liste von Schaltjahren ausgibt.

nyear = 0
for year in range(1860, 2210):
    is_leapyear = ((year % 4 == 0) and (year % 100)) or (year % 400 == 0)
    if is_leapyear:
        nyear = nyear + 1
        if nyear % 12:
            print(year, end=' ')
        else:
            print(year)

1864 1868 1872 1876 1880 1884 1888 1892 1896 1904 1908
1916 1920 1924 1928 1932 1936 1940 1944 1948 1952 1956
1964 1968 1972 1976 1980 1984 1988 1992 1996 2000 2004
2012 2016 2020 2024 2028 2032 2036 2040 2044 2048 2052
2060 2064 2068 2072 2076 2080 2084 2088 2092 2096 2104
2112 2116 2120 2124 2128 2132 2136 2140 2144 2148 2152
2160 2164 2168 2172 2176 2180 2184 2188 2192 2196 2204


In der dritten Zeile wird der logische Ausdruck, der auswertet, ob es sich beidem vorgegebenen Jahr um ein Schaltjahr handelt, der Variable is_leapyear zugewiesen. Nur wenn diese Variable den Wert True besitzt, wird das Jahr ausgegeben. Alternativ hätte man natürlich auch eine Funktion definieren können.

def is_leapyear(year):
    return ((year % 4 == 0) and (year % 100)) or (year % 400 == 0)

nyear = 0
for year in range(1860, 2210):
    if is_leapyear(year):
        nyear = nyear + 1
        if nyear % 12:
            print(year, end=' ')
        else:
            print(year)

1864 1868 1872 1876 1880 1884 1888 1892 1896 1904 1908
1916 1920 1924 1928 1932 1936 1940 1944 1948 1952 1956
1964 1968 1972 1976 1980 1984 1988 1992 1996 2000 2004
2012 2016 2020 2024 2028 2032 2036 2040 2044 2048 2052
2060 2064 2068 2072 2076 2080 2084 2088 2092 2096 2104
2112 2116 2120 2124 2128 2132 2136 2140 2144 2148 2152
2160 2164 2168 2172 2176 2180 2184 2188 2192 2196 2204


Die letzten vier Zeilen dieser beiden Codebeispiele illustrieren zugleich eine Erweiterung der if-Anweisung, in der auch eine Alternative im else-Zweig vorgesehen ist. Falls nyear % 12 den Wahrheitswert True ergibt, also bei der Division von nyear durch 12 ein Rest bleibt, wird der if-Zweig ausgeführt. Nach der Jahreszahl wird dann noch ein Leerzeichen ausgegeben, der Zeilenumbruch entfällt aber. Im allen anderen Fällen, also wenn nyear ohne Rest durch 12 teilbar ist, wird die Anweisung im else-Zweig ausgeführt, so dass nach der Ausgabe der Jahreszahl ein Zeilenumbruch folgt. Auf diese Weise werden zwölf Jahreszahlen je Zeile ausgegeben.

Wichtig ist, dass die else-Anweisung so weit eingerückt ist, wie die zugehörige if-Anweisung. Wäre sie nur einfach eingerückt, würde sie die Alternative zur ersten if-Anweisung bilden. In diesem Fall würde jedes Jahr zwischen 1860 und 2209 mit Ausnahme jedes zwölften Schaltjahres ausgegeben werden. Nach den Schaltjahren würde nur ein Leerzeichen gesetzt werden, aber auf ein Zeilenumbruch verzichtet werden. Dagegen würde nach jedem Jahr, das kein Schaltjahr ist, ein Zeilenumbruch vorgenommen werden. Korrektes Einrücken ist also essentiell dafür, dass der Code wie gewünscht abgearbeitet wird.

nyear = 0
for year in range(1860, 2210):
    is_leapyear = ((year % 4 == 0) and (year % 100)) or (year % 400 == 0)
    if is_leapyear:
        nyear = nyear + 1
        if nyear % 12:
            print(year, end=' ')
    else:
        print(year)

In einfachen Fällen lässt sich eine if … else-Konstruktion auch in einer einzigen Zeile schreiben. Statt

if nyear % 12:
    print(year, end=' ')
else:
    print(year)

könnte man auch

end_string = ' ' if nyear % 12 else ''
print(year, end=end_string)

verwenden.

Die if … else-Konstruktion lässt in der bisher besprochene Weise zwei mögliche Wege abhängig davon zu, ob eine Bedingung erfüllt ist oder nicht. Man kann aber auch mehr als zwei Alternativen vorsehen. Eine erste Möglichkeit, die noch nicht wirklich optimal ist, beruht auf einer Schachtelung von if…else-Verzweigungen.

for n in range(-2, 3):
    if n > 0:
        print(f'{n} ist positiv.')
    else:
        if n == 0:
            print(f'{n} ist gleich null.')
        else:
            print(f'{n} ist negativ.')

-2 ist negativ.
-1 ist negativ.
0 ist gleich null.
1 ist positiv.
2 ist positiv.

Unter Verwendung der elif-Anweisung, die gewissermaßen eine else-Anweisung und eine if-Anweisung zusammenzieht, kann man die Verzweigungen etwas weniger hierarchisch hinschreiben.

for n in range(-2, 3):
    if n > 0:
        print(f'{n} ist positiv.')
    elif n == 0:
        print(f'{n} ist gleich null.')
    else:
        print(f'{n} ist negativ.')

-2 ist negativ.
-1 ist negativ.
0 ist gleich null.
1 ist positiv.
2 ist positiv.

Hierbei werden nacheinander die Bedingungen n > 0 und n == 0 abgeprüft und für den Fall, dass keiner der beiden Ausdrücke gleich True ist, die letzte Alternative ausgeführt. Wichtig ist dabei, dass die Verzweigungsstruktur verlassen wird, sobald eine Bedingung erfüllt war und der zugehörige Code ausgeführt wurde. Dieses Verhalten wird im folgenden Beispiel illustriert.

for n in range(-2, 3):
    if n > 0:
        print(f'{n} ist positiv.')
    elif n % 2 == 0:
        print(f'{n} ist gerade.')
    else:
        print(f'{n} ist negativ und nicht gerade.')

-2 ist gerade.
-1 ist negativ und nicht gerade.
0 ist gerade.
1 ist positiv.
2 ist positiv.

Nachdem die 2 als positive Zahl erkannt und entsprechend behandelt wurde, wurde wegen des in elif enthaltenen else nicht mehr überprüft, ob die Zahl auch gerade ist.

Im Prinzip kann man mehrere elif-Ebenen in einer Verzweigungsstruktur vorsehen. Als erstes muss jedoch immer eine if-Verzweigung stehen. Ein abschließendes else, das alle nicht behandelten Fälle abfängt, kann, muss aber nicht am Ende der Verzweigungsstruktur stehen. Zu bedenken ist allerdings, dass eine lange Hierarchie von Verzweigungen insbesondere dann nicht günstig ist, wenn erst eine der unteren Bedingung erfüllt ist, da dann zunächst einmal viele Bedingungen erfolglos ausgewertet werden müssen. In einem solchen Fall kann zumindest versuchen, dafür zu sorgen, dass die wahrscheinlichsten Fälle weiter oben stehen. In vielen Fällen kann man aber einen zusammengesetzten Datentyp, das so genannte dictionary verwenden, das wir im Kapitel 6.4 genauer besprechen werden.

4.4. Abfangen von Ausnahmen#

In Kapitel 3.2 hatten wir festgestellt, dass Python auf den Versuch, durch null zu teilen, mit einer Ausnahme oder exception reagiert, dem ZeroDivisionError. Unbehandelt führt eine solche Ausnahme zur Ausgabe einer Fehlermeldung und dem Abbruch der Programmausführung. Man kann solche Ausnahmen aber auch in geeigneter Weise behandeln. Zur Illustration betrachten wir die Funktion

\[f(x)=\frac{\sin(x)}{x}\,.\]

Eine numerische Auswertung dieser Funktion an der Stelle \(x=0\) führt zu einer Division durch null und damit zu einem ZeroDivisionError obwohl der Wert der Funktion im Grenzübergang \(x\to 0\) gleich \(1\) ist.

Den speziellen Wert bei \(x=0\) könnte man nun mit Hilfe einer Verzweigung behandeln.

from math import sin

def f(x):
    if x == 0:
        return 1
    else:
        return sin(x)/x

for x in (-0.02, -0.01, 0, 0.01, 0.02):
    print(f"{x:5.2f}  {f(x):8.6f}")

-0.02  0.999933
-0.01  0.999983
 0.00  1.000000
 0.01  0.999983
 0.02  0.999933

Allerdings muss hier jedes Mal überprüft werden, ob \(x=0\) ist, selbst dann, wenn dies in der Anwendung vielleicht nur selten oder überhaupt nicht vorkommt. Dennoch wird man den Spezialfall in vielen Programmiersprachen in dieser Weise behandeln.

In Python folgt man stattdessen meistens dem Motto, dass um Verzeihung zu bitten einfacher ist als um Erlaubnis zu fragen. Anstatt also immer erst zu überprüfen, ob \(x=0\) ist, dividiert man einfach durch \(x\) und kümmert sich dann darum, wenn es Probleme gibt.

from math import sin

def f(x):
    try:
        return sin(x)/x
    except ZeroDivisionError:
        return 1

for x in (-0.02, -0.01, 0, 0.01, 0.02):
    print(f"{x:5.2f}  {f(x):8.6f}")

-0.02  0.999933
-0.01  0.999983
 0.00  1.000000
 0.01  0.999983
 0.02  0.999933

Es wird also zunächst versucht, den Code im try-Block auszuführen. Wenn dabei eine ZeroDivisionError-Ausnahme auftritt, wird der entsprechende Block ausgeführt.

Es ist zwar im Prinzip nicht erforderlich, im Zusammenhang mit except eine oder mehrere Ausnahmen explizit zu benennen. Es ist aber sinnvoll, in der Nennung der Ausnahmen möglichst restriktiv zu sein, da sonst Fehler eventuell unentdeckt bleiben können, wie in dem folgenden Beispiel gezeigt ist.

from math import sin

def f(x):
    try:
        return sin(x)/x
    except:
        return 1

for x in (-0.01, 0, 'xxx'):
    print(f"{x:7}  {f(x):8.6f}")

  -0.01  0.999983
      0  1.000000
xxx      1.000000

Übergibt man als Argument hier eine Zeichenkette, so kommt es bei der Division zu einem TypeError, der hier vom except-Block mit behandelt wird. Besser wäre es, diesen beispielsweise in einem zweiten except-Block separat und adäquat zu behandeln.

Weiterführender Hinweis

Nach dem try- und einem oder mehreren except-Blöcken kann noch ein else- oder ein finally-Block folgen. Der else-Block wird nur dann ausgeführt, wenn keine Ausnahme die Abarbeitung eines except-Blocks erzwingt. Dadurch ist es leicht möglich, den try-Block auf den relevanten Codeteil zu begrenzen. Ein finally-Block wird dagegen immer ausgeführt, zum Beispiel um notwendige Aufräumarbeiten auszuführen.

Abschließend wollen wir noch kurz demonstrieren, wie man Ausnahmen selbst gezielt zur Fehlerbehandlung einsetzen kann. Dazu greifen wir auf die Funktion get_result des Spiels zurück, das wir in Kapitel 2 gesprochen hatten. Dabei mussten die beiden Argumente ganze Zahlen zwischen 0 und 2 einschließlich sein. Für unsere Zwecke nehmen wir an, dass sichergestellt sei, dass die Argumente ganze Zahlen sind. Wir wollen aber den Fehlerfall von Argumenten außerhalb des vorgegebenen Bereichs behandeln.

from random import randrange

def get_result(n_self, n_other):
    if not(0 <= n_self <=2 and 0 <= n_other <= 2):
        raise ValueError(
            f"{n_self = } und {n_other = } müssen beide zwischen 0 und 2 liegen.")
    return (n_self-n_other) % 3

for _ in range(5):
    n_self = randrange(-1, 4)
    n_other = randrange(-1, 4)
    try:
        result = get_result(n_self, n_other)
    except ValueError as e:
        print(e)
    else:
        print(f"Ergebnis für {n_self = } und {n_other = }: {result}")

n_self = 3 und n_other = 1 müssen beide zwischen 0 und 2 liegen.
Ergebnis für n_self = 0 und n_other = 2: 1
Ergebnis für n_self = 2 und n_other = 2: 0
Ergebnis für n_self = 0 und n_other = 2: 1
Ergebnis für n_self = 2 und n_other = 2: 0

Hinweis

In diesem Codebeispiel wird in der for-Schleife ein Unterstrich als Variablenname verwendet. Von dieser Möglichkeit sollte man nur sparsamen Gebrauch machen, da ein Unterstrich im Allgemeinen nicht sehr aussagekräftig ist. Im vorliegenden Fall deutet der Unterstrich an, dass die Laufvariable in der Schleife nicht weiter verwendet wird.

In der Funktion get_result wird mit Hilfe der raise-Anweisung im Fehlerfall eine ValueError-Ausnahme ausgelöst, die zudem eine informative Fehlermeldung enthält. Im aufrufenden Programm wird mit einer try…except-Konstruktion der ValueError abgefangen und die in der hier e genannten Variable enthaltene Fehlermeldung ausgegeben.

Einen Überblick über die von Python vordefinierten Ausnahmen findet man in der Dokumentation der Python-Standardbibliothek. Darüber hinaus ist es auch möglich, eigene Ausnahmen zu definieren.