8. Numerische Programmbibliotheken am Beispiel von NumPy/SciPy#
In den bisherigen Kapiteln hatten wir immer wieder Gelegenheit, auf Möglichkeiten hinzuweisen, die die Python-Standardbibliothek bietet. Wenn man die dort zur Verfügung gestellten Module verwendet, kann man sich Einiges an Arbeit sparen und dabei auch den Code effizienter und übersichtlicher gestalten. Neben der Python-Standardbibliothek gibt es aber auch noch viele interessante Programmpakete, die häufig über den Python Package Index zur Verfügung gestellt werden.
Gerade für Problemstellungen in den Natur- und Ingenieurwissenschaften gibt es
eine oft als scientific ecosystem of Python oder scientific stack
bezeichnete Sammlung von zentralen Paketen. Hierzu gehört als Basispaket
zunächst NumPy, das den Datentyp ndarray sowie Methoden
zur Verfügung stellt, um mit ndarray-Objekten zu arbeiten. Damit wird das
Rechnen mit Vektoren und Matrizen ermöglicht, das wir bei der Besprechung von
Listen in Kapitel 6.1 vermisst hatten.
Ein weiteres wichtiges Paket ist SciPy, das vielfältige numerische Werkzeuge zur Verfügung stellt, beispielsweise zur numerischen Integration oder der Lösung von Differentialgleichungssystemen, zur Lösung von Optimierungsproblemen oder zur Berechnung von speziellen Funktion sowie vielem Anderem mehr. In diesem Kapitel werden wir einen ersten Eindruck von den Möglichkeiten geben, die NumPy und SciPy bereitstellen.
Weitere zentrale Pakete, die in diesem Zusammenhang zu nennen sind, wären Matplotlib zur graphischen Darstellung von Daten, IPython, eine interaktive Python-Konsole, die für das Projekt Jupyter, das unter anderem die Jupyter Notebooks zur Verfügung stellt, von zentraler Bedeutung war und ist, SymPy für das symbolische Rechnen sowie das im Kapitel 7.2 bereits erwähnte pandas, das fortgeschrittene Datenstrukturen und vielfältige Methoden zu einer effizienten Datenanalyse bereithält.
Auf der Basis dieser Pakete haben einzelne wissenschaftliche Disziplinen umfangreiche, auf ihre speziellen Bedürfnisse zugeschnittene Programmpakete entwickelt. So kann Astropy als Standard in der Astronomie angesehen werden. QuTiP, die Quantum Toolbox in Python erlaubt die Simulation von Quantensystemen. Für Problemstellungen, die sich mit finite-Elemente-Methoden lösen lassen, steht FEniCS zur Verfügung. Diese Aufzählung könnte fast beliebig fortgesetzt werden und soll nur dazu dienen, einen allerersten Eindruck von der Vielfalt der zur Verfügung stehenden Python-Programmbibliotheken zu geben.
Nachdem die Benutzung professioneller Programmpakete gelegentlich mit hohen Kosten verbunden sein kann, ist es erwähnenswert, dass die hier aufgeführten Pakete frei verfügbar, aber dennoch von sehr hoher Qualität sind. Zwei Beispiele prominenter Forschungsprojekte, deren Arbeit wesentlich auf einigen der hier genannten Pakete, sind in Kapitel 1.2 genannt. Darüber hinaus ist der Quellcode der Pakete verfügbar, so dass man sich bei Bedarf auch die konkrete Implementierung ansehen sowie zur Weiterentwicklung beitragen kann.
8.1. Installation#
Da NumPy und SciPy nicht in der Python-Standardbibliothek enthalten sind, stehen
diese Programmpakete auch bei einer vorhandenen Python-Installation nicht
automatisch zur Verfügung. Dies lässt sich leicht überprüfen, indem man versucht,
die beiden Pakete zu importieren. Schlägt dies fehl, so erhält man einen
ImportError, der impliziert, dass Python die Pakete nicht finden kann.
Außerdem lässt sich die installierte Version anzeigen, was deswegen interessant
sein kann, weil gelegentlich neue Funktionalität zu den Paketen hinzugefügt
wird. Beachten Sie, dass vor und nach version jeweils zwei Unterstriche
stehen müssen.
import numpy
import scipy
print(f'{numpy.__version__ = }')
print(f'{scipy.__version__ = }')
numpy.__version__ = '2.3.3'
scipy.__version__ = '1.16.2'
Eine einfache und empfehlenswerte Möglichkeit, NumPy und SciPy unter Windows, MacOS oder Linuxvarianten wie Ubuntu verfügbar zu machen, besteht darin, die Anaconda-Distribution zu installieren. Dabei werden allerdings gleichzeitig zahlreiche andere, für wissenschaftliche Zwecke interessante Programmpakete installiert. Ist dies nicht erwünscht, zum Beispiel wegen des relativ großen Bedarfs an Speicherplatz, kann man NumPy und SciPy auch gezielt auf einem der Wege installieren, die in der Installationsanleitung für NumPy und der Installationsanleitung für SciPy beschrieben sind.
8.2. Arrays und Anwendungen#
Für die Arbeit mit dem NumPy-Paket ist es üblich, für numpy die Abkürzung
np einzuführen.
import numpy as np
Dies bedeutet, dass man bei der Verwendung von NumPy vor die entsprechenden
Funktionen jeweils np. setzen muss. Diese Abkürzung verringert den Tippaufwand
und macht zum anderen sofort erkenntlich, wenn es sich um eine Funktion aus dem
NumPy-Paket handelt. Dies ist unter anderem deswegen wichtig, weil NumPy unter
anderem auch Funktionen wie die Exponentialfunktion exp() zur Verfügung
stellt, die von der Exponentialfunktion aus dem math-Modul unterschieden werden
muss.
Das zentrale Objekt, das durch das NumPy-Paket zur Verfügung gestellt wird, ist
das ndarray, wobei die Abkürzung für N-dimensionales Array steht. Hiermit lassen
sich also Vektoren und Matrizen von im Prinzip beliebiger Dimension darstellen,
wobei alle Einträge vom gleichen Datentyp sind.
Es gibt eine ganze Reihe von Möglichkeiten, solche Arrays zu konstruieren. Wir beginnen damit eine Matrix aus einer Liste oder im Allgemeinen Listen von Listen zu erzeugen.
matrixA = np.array([[1.3, 2.5], [-1.7, 3.9]])
print(type(matrixA))
print(matrixA)
<class 'numpy.ndarray'>
[[ 1.3 2.5]
[-1.7 3.9]]
Für ndarrays ist eine Matrixmultiplikation definiert. Um dies zu demonstrieren,
definieren wir ein zweites Array und führen die Matrixmultiplikation aus. Dafür
können wir die Funktion np.dot verwenden oder den @-Operator, der in moderneren
Versionen des NumPy-Pakets definiert ist. Anschließend überprüfen wir das Ergebnis
am 00-Element.
matrixB = np.array([[2.1, -4.5], [0.9, -2.1]])
print(matrixA)
print()
print(matrixB)
print()
print(matrixA @ matrixB)
print()
print(f'{matrixA[0, 0]}*{matrixB[0, 0]} + {matrixA[0, 1]}*{matrixB[1, 0]} = '
f'{matrixA[0, 0]*matrixB[0, 0] + matrixA[0, 1]*matrixB[1, 0]}')
[[ 1.3 2.5]
[-1.7 3.9]]
[[ 2.1 -4.5]
[ 0.9 -2.1]]
[[ 4.98 -11.1 ]
[ -0.06 -0.54]]
1.3*2.1 + 2.5*0.9 = 4.98
Dabei zeigen die letzten beiden Zeilen, wie man Elemente des Arrays adressieren kann, nämlich indem die Indizes für die einzelnen Dimensionen durch Komma getrennt in eckigen Klammern angegeben werden.
Multiplikationsoperatoren @ und *
Beachten Sie, dass der normale Multiplikationsoperator * die beiden Matrizen
elementweise multipliziert und somit keine Matrixmultiplikation ausführt, wie
es @ verlangt. Probieren Sie es an einem Beispiel selbst aus!
Wie bei Listen kann die Adressierung auch mit Hilfe von Slices erfolgen, so dass
man bequem Untermatrizen extrahieren kann. Wichtig dabei ist, dass hier kein neues
Array erzeugt wird, sondern nur eine andere Sicht auf das bereits existierende Array
bereitgestellt wird. Dadurch ist ein solcher Zugriff sehr effizient. In diesem
Beispiel verwenden wird zur schnellen Erzeugung eines etwas größeren Arrays die
arange()-Funktion, die mit mit range() vergleichbar ist, aber eben ein
zunächst eindimensionales Array erzeugt. Dieses können wir dann mit der
reshape()-Methode beispielsweise in ein zweidimensionales Array umwandeln.
matrixC = np.arange(36).reshape(6, 6)
print(matrixC)
print()
print(matrixC[1:3, 3:5])
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]
[24 25 26 27 28 29]
[30 31 32 33 34 35]]
[[ 9 10]
[15 16]]
In der letzten Zeile extrahieren wir eine Untermatrix. Dabei bezieht sich das erste Slice auf die Zeilen und das zweite Slice auf die Spalten. So können wir auch eine Zerlegung in Blockmatrizen vornehmen.
print(matrixC[:3, :3])
print()
print(matrixC[:3, 3:])
print()
print(matrixC[3:, :3])
print()
print(matrixC[3:, 3:])
[[ 0 1 2]
[ 6 7 8]
[12 13 14]]
[[ 3 4 5]
[ 9 10 11]
[15 16 17]]
[[18 19 20]
[24 25 26]
[30 31 32]]
[[21 22 23]
[27 28 29]
[33 34 35]]
Zudem kann die Möglichkeit eines Slices, die Schrittweite anzugeben, verwenden.
print(matrixC[::2, ::3])
[[ 0 3]
[12 15]
[24 27]]
Während wir bei Listen gewohnt sind, diese mit der append()-Methode um weitere
Elemente zu erweitern, sollte man ein solches Vorgehen bei Arrays vermeiden. Da dabei
jeweils ein neues Array erzeugt wird, wäre ein solches Vorgehen äußerst ineffizient.
Stattdessen legt man das Array zunächst in der benötigten Größe an, zum Beispiel mit
Hilfe von np.zeros() oder np.ones(). Das folgende Beispiel illustriert,
wie man die Dimension des Arrays sowie den Datentyp festlegen kann und was die
Multiplikation des Arrays mit einer Zahl bedeutet.
5*np.ones(shape=(2, 3, 4), dtype=np.int64)
array([[[5, 5, 5, 5],
[5, 5, 5, 5],
[5, 5, 5, 5]],
[[5, 5, 5, 5],
[5, 5, 5, 5],
[5, 5, 5, 5]]])
Integer-Arrays
Bei Python sind wir gewohnt, dass Integer im Prinzip beliebig groß werden können.
Bei ndarrays mit Datentyp Integer ist dies nicht der Fall. Der mögliche
Zahlenbereich ist je nach dem gewählten Integertyp eingeschränkt. Genaueres hierzu
findet man in der NumPy-Dokumentation zu Datentypen.
Statt NumPy-Arrays im Detail zu diskutieren, wollen wir im Folgenden einen Eindruck von
einigen Möglichkeiten geben, die dieser Datentyp bietet. Für die Arbeit mit ndarrays
sollten man sich aber auf jeden Fall genauer mit diesen vertraut machen. Wir verweisen
hierzu zum Beispiel auf die NumPy-Dokumentation, aber auch
auf Teil 1 und Teil 2 eines
Videotutorials.
Zu Beginn des Kapitels hatten wir gesehen, wie man Matrizen miteinander multiplizieren kann. Für Vektoren erhält man auf diese Weise unmittelbar das Skalarprodukt. Darüber hinaus kann man auch das Kreuzprodukt und das dyadische Produkt mit Hilfe von NumPy berechnen.
vecA = np.array([2, -3, 0])
vecB = np.array([5, 4, 0])
print(np.dot(vecA, vecB))
print()
print(np.cross(vecA, vecB))
print()
print(np.outer(vecA, vecB))
-2
[ 0 0 23]
[[ 10 8 0]
[-15 -12 0]
[ 0 0 0]]
Statt np.dot() hätten wir natürlich auch wieder den @-Operator verwenden können.
Interessant sind die von NumPy zur Verfügung gestellten universal functions oder ufuncs,
die als Argumente NumPy-Arrays akzeptieren und damit effizient Funktionen in einem Schritt
für eine größere Anzahl von Argumenten auswerten können. In dem folgenden Beispiel demonstrieren
wir zugleich die Verwendung der linspace()-Funktion, um eine Liste äquidistanter Werte
zu erzeugen.
x = np.linspace(0, 2, 11)
print(x)
y = np.exp(x)
print(y)
[0. 0.2 0.4 0.6 0.8 1. 1.2 1.4 1.6 1.8 2. ]
[1. 1.22140276 1.4918247 1.8221188 2.22554093 2.71828183
3.32011692 4.05519997 4.95303242 6.04964746 7.3890561 ]
Die Exponentialfunktion aus dem math-Modul ist dagegen nicht in der Lage, NumPy-Arrays als
Argument zu akzeptieren.
import math
y = math.exp(x)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[11], line 2
1 import math
----> 2 y = math.exp(x)
TypeError: only length-1 arrays can be converted to Python scalars
An dieser Stelle wird deutlich, wie nützlich es sein kann, aus dem Code direkt ersehen zu können, aus welchem Modul die Exponentialfunktion verwendet wird. Das NumPy-Paket stellt ufuncs für die üblichen Standardfunktionen zur Verfügung. Für viele spezielle Funktionen wird man im SciPy-Paket fündig.
Zum Abschluss dieses kurzen Einblicks in das NumPy-Paket wollen wir noch einen Blick auf
häufig benötigte Funktionen aus der linearen Algebra werfen. Diese befinden sich im linalg-Modul
von NumPy, das üblicherweise unter dem Namen LA importiert wird.
from numpy import linalg as LA
Für die Beispiele verwenden wir der Übersichtlichkeit halber nur 2×2-Matrizen, für die wir alle Rechnungen natürlich auch leicht analytisch durchführen könnten. Selbstverständlich kann NumPy auch mit viel größeren Matrizen umgehen. Wir definieren also eine 2×2-Matrix und berechnen zunächst ihre Determinante.
a = np.array([[1, 3], [2, 5]])
print(LA.det(a))
-1.0
Als nächstes berechnen wir die Inverse und obwohl bei diesem Wert der Determinante die Korrektheit des Ergebnisses mehr oder weniger offensichtlich ist, berechnen wir gleich noch das Produkt aus der Matrix und ihrer Inversen, das erwartungsgemäß die Einheitsmatrix ergibt.
a_inv = LA.inv(a)
print(a_inv)
print(a @ a_inv)
[[-5. 3.]
[ 2. -1.]]
[[1. 0.]
[0. 1.]]
Für Anwendungen sehr wichtig ist die Möglichkeit, Eigenwertprobleme zu lösen. Berechnen wir also die Eigenwerte und Eigenvektoren der Matrix.
eigenwerte, eigenvektoren = LA.eig(a)
print(eigenwerte)
print(eigenwerte[0]*eigenwerte[1])
print(eigenvektoren)
[-0.16227766 6.16227766]
-0.9999999999999984
[[-0.93246475 -0.50245469]
[ 0.36126098 -0.86460354]]
der zweiten Ausgabezeile entnehmen als ersten Test, dass das Produkt der Eigenwerte, bis auf Rundungsfehler, gleich der oben erhaltenen Determinanten ist. Überprüfen wir zum Abschluss noch die Korrektheit der Eigenvektoren.
for idx in range(2):
print(a @ eigenvektoren[:, idx],
eigenwerte[idx] * eigenvektoren[:, idx])
[ 0.1513182 -0.05862459] [ 0.1513182 -0.05862459]
[-3.09626531 -5.32792709] [-3.09626531 -5.32792709]
Da der erste Index des Array eigenvektoren der Zeilenindex ist, während der zweite Index der
Spaltenindex ist, sehen wir, dass die Eigenvektoren in diesem Array in den Spalten stehen.
8.3. Numerische Integration#
SciPy ist eine umfangreiche numerische Bibliothek, die wesentlich auf dem gerade besprochenen NumPy-Paket basiert. Sie deckt vielfältige Problemstellungen ab wie zum Beispiel numerische Integration und Lösung von gewöhnlichen Differentialgleichungen, Interpolation, Fouriertransformation, Lösung von Optimierungsproblemen und Nullstellensuche, Signalverarbeitung oder spezielle mathematische Funktionen. Hier wird es uns nur möglich sein, einen ersten Eindruck davon zu geben, wie man mit Hilfe von SciPy numerische Problemstellungen lösen kann. Wir wollen dies anhand der numerischen Auswertung von Integralen sowie der Lösung einer gewöhnlichen Differentialgleichung tun.
In diesem Kapitel wollen wir an zwei Beispielen die Auswertung von Integralen und zeigen und betrachten zunächst das Integral
Das Ergebnis lässt sich durch eine spezielle Funktion, nämlich die Besselfunktion erster Gattung und
nullter Ordnung \(J_0\), an der Stelle angeben. Mit Hilfe des SciPy-Pakets können wir sowohl das
Integral auf der rechten Seite als auch die Besselfunktion auf der linken Seite unabhängig voneinander
auswerten lassen und die beiden Ergebnisse miteinander vergleichen. Betrachten wir zunächst die
numerische Integration. Hierfür steht im integrate-Modul die Funktion quad() zur Verfügung,
die als wesentliche Argumente den Integranden und die Integrationsgrenzen erwartet. Darüber hinaus
gibt es noch weitere Argumente, die wir hier einfach auf ihren Defaultwerten belassen. Den Integranden
stellen wir mit Hilfe einer Lambdafunktion zur Verfügung.
from math import cos, pi
from scipy.integrate import quad
resultat, fehler = quad(lambda x: cos(cos(x))/pi, 0, pi)
print(resultat, fehler)
0.7651976865579665 7.610963315273956e-11
Wir erhalten sowohl das Resultat des numerischen Fehlers als auch eine Abschätzung für den absoluten Integrationsfehler.
Zum Vergleich werten wir die Besselfunktion \(J_0\) nun direkt an der Stelle 1 aus. Dazu importieren
wir die entsprechende Funktion aus dem special-Modul von SciPy.
from scipy.special import j0
print(j0(1))
0.7651976865579665
In diesem Fall stimmen die beiden Ergebnisse perfekt überein, was aber im Allgemeinen nicht erwartet werden kann. Problematisch sind insbesondere Integranden, die Singularitäten enthalten oder sehr schnell oszillieren.
Um zu demonstrieren, dass SciPy auch mit uneigentlichen Integralen umgehen kann, betrachten wir noch das Integral
dessen Wert man ebenfalls analytisch kennt. Dies erlaubt uns wiederum, einen Eindruck davon zu gewinnen,
wie gut das Integrationsergebnis ist. Um mit den Integrationsgrenzen umzugehen, verwenden wir die
Konstante inf aus NumPy.
import numpy as np
resultat, fehler = quad(lambda x: 1/(x*x+1), -np.inf, np.inf)
print(resultat, fehler)
print(pi)
3.141592653589793 5.155583041103855e-10
3.141592653589793
Auch in diesem Fall ist die Übereinstimmung perfekt, so dass wir nochmals betonen wollen, dass dies im Allgemeinen keineswegs zu erwarten ist.
Neben der Funktion quad() stellt noch weitere Funktionen zur Verfügung, in denen zum Beispiel
andere Integrationsverfahren verwendet werden oder mit denen auch mehrdimensionale Integrale
berechnet werden können. Weitere Informationen findet man in der Dokumentation des
scipy.integrate-Moduls.
8.4. Integration gewöhnlicher Differentialgleichungen#
In Natur- und Ingenieurwissenschaften steht man häufig vor der Aufgabe, Differentialgleichungen numerisch
zu lösen, wobei zwischen gewöhnlichen und partiellen Differentialgleichungen sowie zwischen Anfangs- und
Randwertproblemen unterschieden werden muss. In diesem Kapitel wollen wir anhand von zwei Beispielen zeigen,
wie mit Hilfe von SciPy gewöhnliche Differentialgleichungen mit Anfangsbedingungen gelöst werden können.
Dazu werden wir die Funktion solve_ivp() aus dem integrate-Modul verwenden, wobei ivp als Abkürzung
für initial value problem zu lesen ist.
Zunächst ist es sinnvoll, sich darüber zu informieren, wie diese Funktion aufzurufen ist.
from scipy.integrate import solve_ivp
help(solve_ivp)
Help on function solve_ivp in module scipy.integrate._ivp.ivp:
solve_ivp(
fun,
t_span,
y0,
method='RK45',
t_eval=None,
dense_output=False,
events=None,
vectorized=False,
args=None,
**options
)
Solve an initial value problem for a system of ODEs.
This function numerically integrates a system of ordinary differential
equations given an initial value::
dy / dt = f(t, y)
y(t0) = y0
Here t is a 1-D independent variable (time), y(t) is an
N-D vector-valued function (state), and an N-D
vector-valued function f(t, y) determines the differential equations.
The goal is to find y(t) approximately satisfying the differential
equations, given an initial value y(t0)=y0.
Some of the solvers support integration in the complex domain, but note
that for stiff ODE solvers, the right-hand side must be
complex-differentiable (satisfy Cauchy-Riemann equations [11]_).
To solve a problem in the complex domain, pass y0 with a complex data type.
Another option always available is to rewrite your problem for real and
imaginary parts separately.
Parameters
----------
fun : callable
Right-hand side of the system: the time derivative of the state ``y``
at time ``t``. The calling signature is ``fun(t, y)``, where ``t`` is a
scalar and ``y`` is an ndarray with ``len(y) = len(y0)``. Additional
arguments need to be passed if ``args`` is used (see documentation of
``args`` argument). ``fun`` must return an array of the same shape as
``y``. See `vectorized` for more information.
t_span : 2-member sequence
Interval of integration (t0, tf). The solver starts with t=t0 and
integrates until it reaches t=tf. Both t0 and tf must be floats
or values interpretable by the float conversion function.
y0 : array_like, shape (n,)
Initial state. For problems in the complex domain, pass `y0` with a
complex data type (even if the initial value is purely real).
method : string or `OdeSolver`, optional
Integration method to use:
* 'RK45' (default): Explicit Runge-Kutta method of order 5(4) [1]_.
The error is controlled assuming accuracy of the fourth-order
method, but steps are taken using the fifth-order accurate
formula (local extrapolation is done). A quartic interpolation
polynomial is used for the dense output [2]_. Can be applied in
the complex domain.
* 'RK23': Explicit Runge-Kutta method of order 3(2) [3]_. The error
is controlled assuming accuracy of the second-order method, but
steps are taken using the third-order accurate formula (local
extrapolation is done). A cubic Hermite polynomial is used for the
dense output. Can be applied in the complex domain.
* 'DOP853': Explicit Runge-Kutta method of order 8 [13]_.
Python implementation of the "DOP853" algorithm originally
written in Fortran [14]_. A 7-th order interpolation polynomial
accurate to 7-th order is used for the dense output.
Can be applied in the complex domain.
* 'Radau': Implicit Runge-Kutta method of the Radau IIA family of
order 5 [4]_. The error is controlled with a third-order accurate
embedded formula. A cubic polynomial which satisfies the
collocation conditions is used for the dense output.
* 'BDF': Implicit multi-step variable-order (1 to 5) method based
on a backward differentiation formula for the derivative
approximation [5]_. The implementation follows the one described
in [6]_. A quasi-constant step scheme is used and accuracy is
enhanced using the NDF modification. Can be applied in the
complex domain.
* 'LSODA': Adams/BDF method with automatic stiffness detection and
switching [7]_, [8]_. This is a wrapper of the Fortran solver
from ODEPACK.
Explicit Runge-Kutta methods ('RK23', 'RK45', 'DOP853') should be used
for non-stiff problems and implicit methods ('Radau', 'BDF') for
stiff problems [9]_. Among Runge-Kutta methods, 'DOP853' is recommended
for solving with high precision (low values of `rtol` and `atol`).
If not sure, first try to run 'RK45'. If it makes unusually many
iterations, diverges, or fails, your problem is likely to be stiff and
you should use 'Radau' or 'BDF'. 'LSODA' can also be a good universal
choice, but it might be somewhat less convenient to work with as it
wraps old Fortran code.
You can also pass an arbitrary class derived from `OdeSolver` which
implements the solver.
t_eval : array_like or None, optional
Times at which to store the computed solution, must be sorted and lie
within `t_span`. If None (default), use points selected by the solver.
dense_output : bool, optional
Whether to compute a continuous solution. Default is False.
events : callable, or list of callables, optional
Events to track. If None (default), no events will be tracked.
Each event occurs at the zeros of a continuous function of time and
state. Each function must have the signature ``event(t, y)`` where
additional argument have to be passed if ``args`` is used (see
documentation of ``args`` argument). Each function must return a
float. The solver will find an accurate value of `t` at which
``event(t, y(t)) = 0`` using a root-finding algorithm. By default,
all zeros will be found. The solver looks for a sign change over
each step, so if multiple zero crossings occur within one step,
events may be missed. Additionally each `event` function might
have the following attributes:
terminal: bool or int, optional
When boolean, whether to terminate integration if this event occurs.
When integral, termination occurs after the specified the number of
occurrences of this event.
Implicitly False if not assigned.
direction: float, optional
Direction of a zero crossing. If `direction` is positive,
`event` will only trigger when going from negative to positive,
and vice versa if `direction` is negative. If 0, then either
direction will trigger event. Implicitly 0 if not assigned.
You can assign attributes like ``event.terminal = True`` to any
function in Python.
vectorized : bool, optional
Whether `fun` can be called in a vectorized fashion. Default is False.
If ``vectorized`` is False, `fun` will always be called with ``y`` of
shape ``(n,)``, where ``n = len(y0)``.
If ``vectorized`` is True, `fun` may be called with ``y`` of shape
``(n, k)``, where ``k`` is an integer. In this case, `fun` must behave
such that ``fun(t, y)[:, i] == fun(t, y[:, i])`` (i.e. each column of
the returned array is the time derivative of the state corresponding
with a column of ``y``).
Setting ``vectorized=True`` allows for faster finite difference
approximation of the Jacobian by methods 'Radau' and 'BDF', but
will result in slower execution for other methods and for 'Radau' and
'BDF' in some circumstances (e.g. small ``len(y0)``).
args : tuple, optional
Additional arguments to pass to the user-defined functions. If given,
the additional arguments are passed to all user-defined functions.
So if, for example, `fun` has the signature ``fun(t, y, a, b, c)``,
then `jac` (if given) and any event functions must have the same
signature, and `args` must be a tuple of length 3.
**options
Options passed to a chosen solver. All options available for already
implemented solvers are listed below.
first_step : float or None, optional
Initial step size. Default is `None` which means that the algorithm
should choose.
max_step : float, optional
Maximum allowed step size. Default is np.inf, i.e., the step size is not
bounded and determined solely by the solver.
rtol, atol : float or array_like, optional
Relative and absolute tolerances. The solver keeps the local error
estimates less than ``atol + rtol * abs(y)``. Here `rtol` controls a
relative accuracy (number of correct digits), while `atol` controls
absolute accuracy (number of correct decimal places). To achieve the
desired `rtol`, set `atol` to be smaller than the smallest value that
can be expected from ``rtol * abs(y)`` so that `rtol` dominates the
allowable error. If `atol` is larger than ``rtol * abs(y)`` the
number of correct digits is not guaranteed. Conversely, to achieve the
desired `atol` set `rtol` such that ``rtol * abs(y)`` is always smaller
than `atol`. If components of y have different scales, it might be
beneficial to set different `atol` values for different components by
passing array_like with shape (n,) for `atol`. Default values are
1e-3 for `rtol` and 1e-6 for `atol`.
jac : array_like, sparse_matrix, callable or None, optional
Jacobian matrix of the right-hand side of the system with respect
to y, required by the 'Radau', 'BDF' and 'LSODA' method. The
Jacobian matrix has shape (n, n) and its element (i, j) is equal to
``d f_i / d y_j``. There are three ways to define the Jacobian:
* If array_like or sparse_matrix, the Jacobian is assumed to
be constant. Not supported by 'LSODA'.
* If callable, the Jacobian is assumed to depend on both
t and y; it will be called as ``jac(t, y)``, as necessary.
Additional arguments have to be passed if ``args`` is
used (see documentation of ``args`` argument).
For 'Radau' and 'BDF' methods, the return value might be a
sparse matrix.
* If None (default), the Jacobian will be approximated by
finite differences.
It is generally recommended to provide the Jacobian rather than
relying on a finite-difference approximation.
jac_sparsity : array_like, sparse matrix or None, optional
Defines a sparsity structure of the Jacobian matrix for a finite-
difference approximation. Its shape must be (n, n). This argument
is ignored if `jac` is not `None`. If the Jacobian has only few
non-zero elements in *each* row, providing the sparsity structure
will greatly speed up the computations [10]_. A zero entry means that
a corresponding element in the Jacobian is always zero. If None
(default), the Jacobian is assumed to be dense.
Not supported by 'LSODA', see `lband` and `uband` instead.
lband, uband : int or None, optional
Parameters defining the bandwidth of the Jacobian for the 'LSODA'
method, i.e., ``jac[i, j] != 0 only for i - lband <= j <= i + uband``.
Default is None. Setting these requires your jac routine to return the
Jacobian in the packed format: the returned array must have ``n``
columns and ``uband + lband + 1`` rows in which Jacobian diagonals are
written. Specifically ``jac_packed[uband + i - j , j] = jac[i, j]``.
The same format is used in `scipy.linalg.solve_banded` (check for an
illustration). These parameters can be also used with ``jac=None`` to
reduce the number of Jacobian elements estimated by finite differences.
min_step : float, optional
The minimum allowed step size for 'LSODA' method.
By default `min_step` is zero.
Returns
-------
Bunch object with the following fields defined:
t : ndarray, shape (n_points,)
Time points.
y : ndarray, shape (n, n_points)
Values of the solution at `t`.
sol : `OdeSolution` or None
Found solution as `OdeSolution` instance; None if `dense_output` was
set to False.
t_events : list of ndarray or None
Contains for each event type a list of arrays at which an event of
that type event was detected. None if `events` was None.
y_events : list of ndarray or None
For each value of `t_events`, the corresponding value of the solution.
None if `events` was None.
nfev : int
Number of evaluations of the right-hand side.
njev : int
Number of evaluations of the Jacobian.
nlu : int
Number of LU decompositions.
status : int
Reason for algorithm termination:
* -1: Integration step failed.
* 0: The solver successfully reached the end of `tspan`.
* 1: A termination event occurred.
message : string
Human-readable description of the termination reason.
success : bool
True if the solver reached the interval end or a termination event
occurred (``status >= 0``).
References
----------
.. [1] J. R. Dormand, P. J. Prince, "A family of embedded Runge-Kutta
formulae", Journal of Computational and Applied Mathematics, Vol. 6,
No. 1, pp. 19-26, 1980.
.. [2] L. W. Shampine, "Some Practical Runge-Kutta Formulas", Mathematics
of Computation,, Vol. 46, No. 173, pp. 135-150, 1986.
.. [3] P. Bogacki, L.F. Shampine, "A 3(2) Pair of Runge-Kutta Formulas",
Appl. Math. Lett. Vol. 2, No. 4. pp. 321-325, 1989.
.. [4] E. Hairer, G. Wanner, "Solving Ordinary Differential Equations II:
Stiff and Differential-Algebraic Problems", Sec. IV.8.
.. [5] `Backward Differentiation Formula
<https://en.wikipedia.org/wiki/Backward_differentiation_formula>`_
on Wikipedia.
.. [6] L. F. Shampine, M. W. Reichelt, "THE MATLAB ODE SUITE", SIAM J. SCI.
COMPUTE., Vol. 18, No. 1, pp. 1-22, January 1997.
.. [7] A. C. Hindmarsh, "ODEPACK, A Systematized Collection of ODE
Solvers," IMACS Transactions on Scientific Computation, Vol 1.,
pp. 55-64, 1983.
.. [8] L. Petzold, "Automatic selection of methods for solving stiff and
nonstiff systems of ordinary differential equations", SIAM Journal
on Scientific and Statistical Computing, Vol. 4, No. 1, pp. 136-148,
1983.
.. [9] `Stiff equation <https://en.wikipedia.org/wiki/Stiff_equation>`_ on
Wikipedia.
.. [10] A. Curtis, M. J. D. Powell, and J. Reid, "On the estimation of
sparse Jacobian matrices", Journal of the Institute of Mathematics
and its Applications, 13, pp. 117-120, 1974.
.. [11] `Cauchy-Riemann equations
<https://en.wikipedia.org/wiki/Cauchy-Riemann_equations>`_ on
Wikipedia.
.. [12] `Lotka-Volterra equations
<https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations>`_
on Wikipedia.
.. [13] E. Hairer, S. P. Norsett G. Wanner, "Solving Ordinary Differential
Equations I: Nonstiff Problems", Sec. II.
.. [14] `Page with original Fortran code of DOP853
<http://www.unige.ch/~hairer/software.html>`_.
Examples
--------
Basic exponential decay showing automatically chosen time points.
>>> import numpy as np
>>> from scipy.integrate import solve_ivp
>>> def exponential_decay(t, y): return -0.5 * y
>>> sol = solve_ivp(exponential_decay, [0, 10], [2, 4, 8])
>>> print(sol.t)
[ 0. 0.11487653 1.26364188 3.06061781 4.81611105 6.57445806
8.33328988 10. ]
>>> print(sol.y)
[[2. 1.88836035 1.06327177 0.43319312 0.18017253 0.07483045
0.03107158 0.01350781]
[4. 3.7767207 2.12654355 0.86638624 0.36034507 0.14966091
0.06214316 0.02701561]
[8. 7.5534414 4.25308709 1.73277247 0.72069014 0.29932181
0.12428631 0.05403123]]
Specifying points where the solution is desired.
>>> sol = solve_ivp(exponential_decay, [0, 10], [2, 4, 8],
... t_eval=[0, 1, 2, 4, 10])
>>> print(sol.t)
[ 0 1 2 4 10]
>>> print(sol.y)
[[2. 1.21305369 0.73534021 0.27066736 0.01350938]
[4. 2.42610739 1.47068043 0.54133472 0.02701876]
[8. 4.85221478 2.94136085 1.08266944 0.05403753]]
Cannon fired upward with terminal event upon impact. The ``terminal`` and
``direction`` fields of an event are applied by monkey patching a function.
Here ``y[0]`` is position and ``y[1]`` is velocity. The projectile starts
at position 0 with velocity +10. Note that the integration never reaches
t=100 because the event is terminal.
>>> def upward_cannon(t, y): return [y[1], -0.5]
>>> def hit_ground(t, y): return y[0]
>>> hit_ground.terminal = True
>>> hit_ground.direction = -1
>>> sol = solve_ivp(upward_cannon, [0, 100], [0, 10], events=hit_ground)
>>> print(sol.t_events)
[array([40.])]
>>> print(sol.t)
[0.00000000e+00 9.99900010e-05 1.09989001e-03 1.10988901e-02
1.11088891e-01 1.11098890e+00 1.11099890e+01 4.00000000e+01]
Use `dense_output` and `events` to find position, which is 100, at the apex
of the cannonball's trajectory. Apex is not defined as terminal, so both
apex and hit_ground are found. There is no information at t=20, so the sol
attribute is used to evaluate the solution. The sol attribute is returned
by setting ``dense_output=True``. Alternatively, the `y_events` attribute
can be used to access the solution at the time of the event.
>>> def apex(t, y): return y[1]
>>> sol = solve_ivp(upward_cannon, [0, 100], [0, 10],
... events=(hit_ground, apex), dense_output=True)
>>> print(sol.t_events)
[array([40.]), array([20.])]
>>> print(sol.t)
[0.00000000e+00 9.99900010e-05 1.09989001e-03 1.10988901e-02
1.11088891e-01 1.11098890e+00 1.11099890e+01 4.00000000e+01]
>>> print(sol.sol(sol.t_events[1][0]))
[100. 0.]
>>> print(sol.y_events)
[array([[-5.68434189e-14, -1.00000000e+01]]),
array([[1.00000000e+02, 1.77635684e-15]])]
As an example of a system with additional parameters, we'll implement
the Lotka-Volterra equations [12]_.
>>> def lotkavolterra(t, z, a, b, c, d):
... x, y = z
... return [a*x - b*x*y, -c*y + d*x*y]
...
We pass in the parameter values a=1.5, b=1, c=3 and d=1 with the `args`
argument.
>>> sol = solve_ivp(lotkavolterra, [0, 15], [10, 5], args=(1.5, 1, 3, 1),
... dense_output=True)
Compute a dense solution and plot it.
>>> t = np.linspace(0, 15, 300)
>>> z = sol.sol(t)
>>> import matplotlib.pyplot as plt
>>> plt.plot(t, z.T)
>>> plt.xlabel('t')
>>> plt.legend(['x', 'y'], shadow=True)
>>> plt.title('Lotka-Volterra System')
>>> plt.show()
A couple examples of using solve_ivp to solve the differential
equation ``y' = Ay`` with complex matrix ``A``.
>>> A = np.array([[-0.25 + 0.14j, 0, 0.33 + 0.44j],
... [0.25 + 0.58j, -0.2 + 0.14j, 0],
... [0, 0.2 + 0.4j, -0.1 + 0.97j]])
Solving an IVP with ``A`` from above and ``y`` as 3x1 vector:
>>> def deriv_vec(t, y):
... return A @ y
>>> result = solve_ivp(deriv_vec, [0, 25],
... np.array([10 + 0j, 20 + 0j, 30 + 0j]),
... t_eval=np.linspace(0, 25, 101))
>>> print(result.y[:, 0])
[10.+0.j 20.+0.j 30.+0.j]
>>> print(result.y[:, -1])
[18.46291039+45.25653651j 10.01569306+36.23293216j
-4.98662741+80.07360388j]
Solving an IVP with ``A`` from above with ``y`` as 3x3 matrix :
>>> def deriv_mat(t, y):
... return (A @ y.reshape(3, 3)).flatten()
>>> y0 = np.array([[2 + 0j, 3 + 0j, 4 + 0j],
... [5 + 0j, 6 + 0j, 7 + 0j],
... [9 + 0j, 34 + 0j, 78 + 0j]])
>>> result = solve_ivp(deriv_mat, [0, 25], y0.flatten(),
... t_eval=np.linspace(0, 25, 101))
>>> print(result.y[:, 0].reshape(3, 3))
[[ 2.+0.j 3.+0.j 4.+0.j]
[ 5.+0.j 6.+0.j 7.+0.j]
[ 9.+0.j 34.+0.j 78.+0.j]]
>>> print(result.y[:, -1].reshape(3, 3))
[[ 5.67451179 +12.07938445j 17.2888073 +31.03278837j
37.83405768 +63.25138759j]
[ 3.39949503 +11.82123994j 21.32530996 +44.88668871j
53.17531184+103.80400411j]
[ -2.26105874 +22.19277664j -15.1255713 +70.19616341j
-38.34616845+153.29039931j]]
Wichtig für uns ist insbesondere die Beschreibung zu Beginn des Hilfetexts sowie die ersten Argumente. Für die weiter hinten stehenden Argumente ist es zunächst sinnvoll, die Defaultwerte zu belassen. Interessant ist aber auch das Ende des Hilfetexts, wo einige konkrete Beispiele aufgeführt werden.
Wie wir der Beschreibung entnehmen können, ist solve_ivp() in der Lage, Systeme gewöhnlicher
Differentialgleichungen zu lösen. Wir wollen mit dem einfachsten Fall, nämlich einer einzigen
Differentialgleichung erster Ordnung, beginnen. Konkret wollen wir die Differentialgleichung
mit der Anfangsbedingung \(x(0)=1\) lösen. Hierbei handelt es sich um eine nichtlineare Differentialgleichung, die sich mittels des Verfahrens der Trennung der Variablen analytisch lösen lässt. Die zugehörige Lösung
erlaubt es uns, die Qualität der numerischen Lösung einzuschätzen. Wie wir dem Hilfetext entnehmen können, besitzen die ersten drei Argumente keinen Defaultwert, so dass wir diese Argumente auf jeden Fall spezifizieren müssen. Dabei handelt es sich um die Funktion auf der rechten Seite der Differentialgleichung
um ein Tupel, das die Anfangszeit \(t_\text{i}\) und die Endzeit \(t_\text{f}\) enthält, sowie den oder die Anfangswerte \(y(0)\). Zu beachten ist, dass \(t\) eine allgemeine unabhängige Variable ist, also keineswegs die Bedeutung einer Zeit haben muss. \(y\) ist in unserem Fall eine skalare Funktion, für Systeme von Differentialgleichungen dagegen eine vektorwertige Funktion. Entsprechend ist \(y(0)\) entweder ein Skalar oder ein Vektor.
Damit sind wir nun in der Lage, solve_ivp() zur Lösung unserer Differentialgleichung einzusetzen.
Um hinreichend viele Datenpunkte für eine graphische Darstellung zu erhalten, wollen wir außerdem die
gewünschten Zeitpunkte festlegen, zu denen die Lösung ausgegeben wird.
import numpy as np
t_span = (0, 5)
y0 = [1]
t_eval = np.linspace(*t_span, 100)
sol = solve_ivp(lambda t, y: -y*y, t_span, y0, t_eval=t_eval)
An dieser Stelle sind noch ein paar Anmerkungen sinnvoll. Der Anfangswert y0 muss laut Hilfetext immer
Array-artig sein, und wir verwenden daher hier einfach eine Liste mit einem Element. t_eval enthält die
uns interessierenden Zeitpunkte, wobei im ersten Argument der linspace() der Stern bedeutet, dass
das Tupel t_span ausgepackt wird. Dies erspart es uns, explizit t_span[0] und t_span[1] anzugeben.
Das Argument t_eval können wir hier nicht über die Position übergeben, da sonst als viertes Argument
zunächst die Lösungsmethode angegeben werden müssen. Wir belassen es hier bei der defaultmäßig vorgesehenen
Runge-Kutta-Methode. Schließlich entnehmen wir dem Hilfetext, dass sol eine ganze Reihe von Informationen
über die Lösung enthält. Uns interessiert natürlich besonders die Lösung, die in sol.y enthalten ist.
Damit können wir nun die numerische Lösung graphisch darstellen und mit der analytischen Lösung vergleichen.
import matplotlib.pyplot as plt
y_analytisch = 1/(1+t_eval)
plt.plot(t_eval, sol.y[0], 'o')
plt.plot(t_eval, y_analytisch)
plt.show()
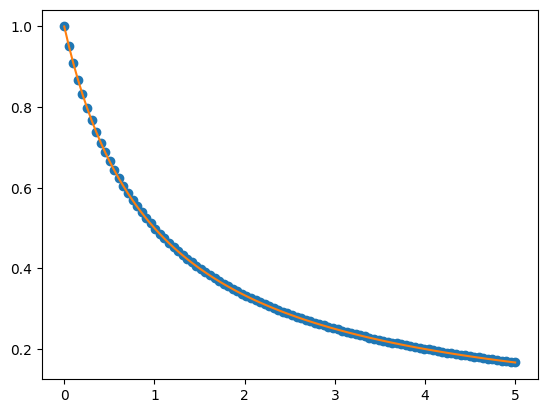
Da es schwierig ist, den Fehler der durch die blauen Punkte dargestellten numerischen Lösung im Vergleich zur als orangefarbige Linie dargestellten analytischen Lösung mit bloßem Auge zu beurteilen, stellen wir auch noch den relativen Fehler dar.
plt.plot(t_eval, 1-sol.y[0]/y_analytisch)
plt.show()
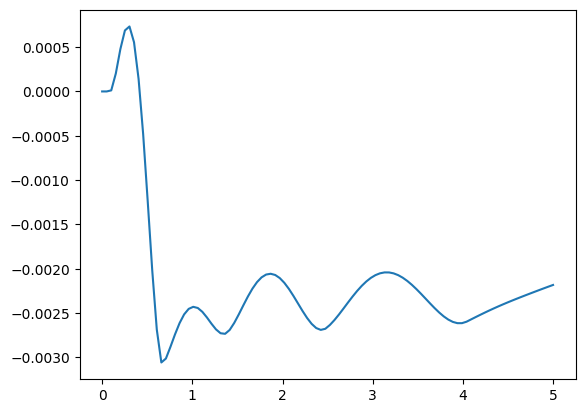
Aus der Abbildung lässt sich entnehmen, dass der relative Fehler hier immerhin bis zu 3‰ beträgt.
Auf den ersten Blick könnte man meinen, dass solve_ivp() nur zur Lösung von Differentialgleichungen
erster Ordnung geeignet ist. Wie sieht es also zum Beispiel mit der Lösung der Bewegungsgleichung eines
gedämpften harmonischen Oszillators
aus? Der Trick besteht darin, diese Differentialgleichung zweiter Ordnung durch Einführung der Geschwindigkeit als Hilfsvariable in zwei Differentialgleichungen erster Ordnung umzuschreiben, womit wir ein System gewöhnlicher Differentialgleichungen erster Ordnung
erhalten. Dieses können wir mit Hilfe von solve_ivp() lösen. Als Anfangsbedingungen wollen wir
\(x(0) = 0, v(0) = 1\) wählen, das gedämpfte Pendel also in der Ruhelage anstoßen. Natürlich hätten wir
eine kompliziertere Differentialgleichung wählen können, für die keine analytische Lösung zur Verfügung
steht. Wir wollen aber auch hier am Ende die numerische mit der analytischen Lösung vergleichen.
def ableitung(t, y, alpha):
x, v = y
return [v, -x-alpha*v]
t_span = (0, 20)
t_eval = np.linspace(*t_span, 300)
anfangsbedingungen = [0, 1]
alpha = 0.3
sol = solve_ivp(ableitung, t_span, anfangsbedingungen, t_eval=t_eval, args=(alpha,))
plt.plot(t_eval, sol.y[0])
plt.plot(t_eval, sol.y[1])
plt.show()
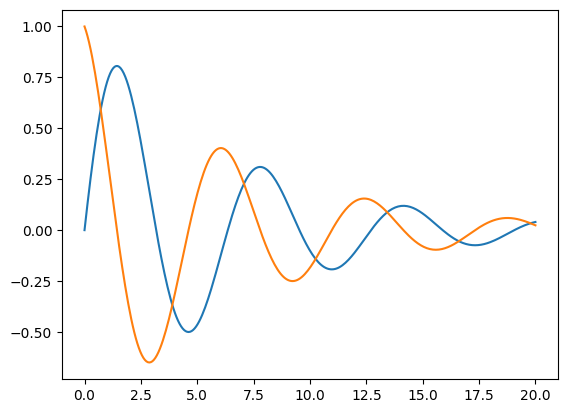
Im Gegensatz zum ersten Beispiel verlangt die Funktion, die wir hier ableitung genannt haben, neben
den Argumenten t und y noch den Parameter alpha. Dieser wird in einem Tupel an das Argument args
von solve_ivp() übergeben. Die Lösung in sol.y ist ein Vektor, so dass wir bereits im ersten
Beispiel explizit sol.y[0] angeben mussten, um die Lösungsfunktion zu erhalten. Hier können wir nun
sowohl den Ort (blau dargestellt) als auch die Geschwindigkeit (orange dargestellt) als Komponenten
extrahieren.
Sehen wir uns abschließend noch die Differenz zur analytischen Lösung an.
def y_analytisch(t, alpha):
omega = np.sqrt(1-0.25*alpha**2)
return np.exp(-0.5*alpha*t)*np.sin(omega*t)/omega
plt.plot(t_eval, sol.y[0]-y_analytisch(t_eval, alpha))
plt.show()
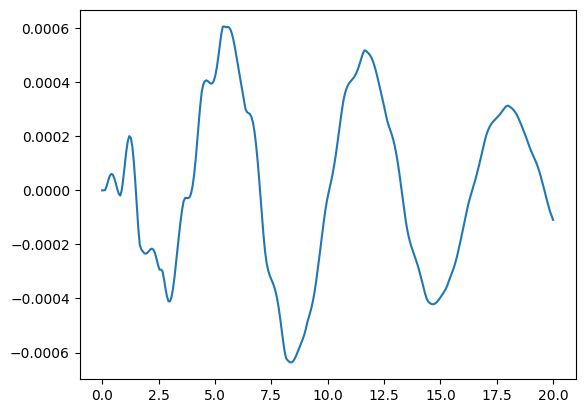
Auch in diesem Fall erhalten wir einen Fehler von einigen Promille. Benötigt man eine genauere Lösung,
so kann die Parameter atol für den absoluten Fehler und rtol für den relativen Fehler entsprechend
anpassen. Weitere Informationen hierzu finden sich in obigem Hilfetext zu solve_ivp().
Zum Abschluss dieses Kapitels betonen wir noch einmal, dass wir hier nur einen winzigen Eindruck von den vielfältigen Möglichkeiten geben konnten, die NumPy und SciPy bieten. Es lohnt sich daher, einen Blick in die Dokumentation von NumPy und die Dokumentation von SciPy oder zumindest die Überschriften der API-Dokumentation von SciPy zu werfen.
