NumPy¶
In der Vorlesung »Einführung in das Programmieren für Physiker und Naturwissenschaftler« wurde am Beispiel von NumPy und SciPy eine kurze Einführung in die Benutzung numerischer Programmbibliotheken gegeben. Dabei wurde an einigen wenigen Beispielen gezeigt, wie man in Python mit Vektoren und Matrizen arbeiten und einfache Problemstellungen der linearen Algebra lösen kann. Im Folgenden wollen wir uns etwas genauer mit NumPy beschäftigen, das die Basis für wichtige wissenschaftliche Programmbibliotheken bildet, wie das bereits genannte SciPy, Matplotlib für die Erstellung von Grafiken, Pandas für die Analyse großer Datenmengen, Scikit-image für die Bildbearbeitung, Scikit-learn für maschinenbasiertes Lernen und einige andere mehr.
Wegen des großen Umfangs der von NumPy zur Verfügung gestellten Funktionalität werden wir uns auf wesentliche Aspekte beschränken und keine vollständige Beschreibung anstreben. Bei Bedarf sollte daher die NumPy Referenzdokumentation herangezogen werden. Als Informationsquelle sind zudem die Python Scientific Lecture Notes empfehlenswert. Dort werden auch weitere Programmbibliotheken diskutiert, die in naturwissenschaftlichen Anwendungen hilfreich sein können.
Python-Listen und Matrizen¶
Viele naturwissenschaftliche Problemstellungen lassen sich in natürlicher Weise mit Hilfe von Vektoren und Matrizen formulieren. Dies kann entweder eine Eigenschaft des ursprünglichen Problems sein, beispielsweise bei der Beschreibung eines gekoppelten schwingenden Systems mit Hilfe von gekoppelten Differentialgleichungen. Es kann aber auch vorkommen, dass erst die numerische Umsetzung zu einer Formulierung in Vektoren und Matrizen führt, zum Beispiel bei der Diskretisierung einer partiellen Differentialgleichung.
Will man solche Problemstellungen mit den Standardmitteln bearbeiten, die von Python zur Verfügung gestellt werden, so wird man auf Listen zurückgreifen müssen. Um eine zweidimensionale Matrix zu definieren, würde man eine Liste von Listen anlegen und könnte dann durch eine doppelte Indizierung auf ein einzelnes Element zugreifen.
In [1]: matrix = [[1.1, 2.2, 3.3], [4.4, 5.5, 6.6], [7.7, 8.8, 9.9]]
In [2]: matrix[0]
Out[2]: [1.1, 2.2, 3.3]
In [3]: matrix[0][2]
Out[3]: 3.3
Das Beispiel erklärt die doppelte Indizierung. Durch den ersten Index, hier [0], wird
die erste Unterliste ausgewählt, aus der wiederum ein einzelnes Element, hier das dritte,
ausgewählt werden kann.
Eine Zeile kann man entweder wie oben in der Eingabe 2 erhalten oder auch etwas umständlicher mit
In [4]: matrix[0][:]
Out[4]: [1.1, 2.2, 3.3]
Hier ist explizit angegeben, dass wir alle Elemente der ersten Zeile haben wollen. Ein enstprechender Zugriff auf eine Spalte funktioniert jedoch nicht:
In [5]: matrix[:][0]
Out[5]: [1.1, 2.2, 3.3]
Hier gibt matrix[:] eine Liste mit allen Unterlisten, also einfach die
ursprüngliche Liste zurück. Somit ist matrix[:][0] nichts anderes als die
erste Unterliste. Wir erhalten also wiederum die erste Zeile und keineswegs die
erste Spalte. Auch wenn es beispielsweise mit Hilfe einer list comprehension
möglich ist, eine Spalte aus einer Matrix zu extrahieren, zeigt das Beispiel,
dass Zeilen und Spalten in einer durch eine Liste dargestellten Matrix nicht in
gleicher Weise behandelt werden können. Für eine Matrix würde man eine
Gleichbehandlung jedoch auf jeden Fall erwarten.
Ein weiterer Nachteil besteht in der Flexibilität von Listen, die ja bekanntlich beliebige
Objekte enthalten können. Python muss daher einen erheblichen Aufwand bei der Verwaltung
von Listen treiben. Dies betrifft alleine schon die Adressierung eines einzelnen Elements.
Andererseits wird diese Flexibilität bei Matrizen überhaupt nicht benötigt, da dort alle
Einträge vom gleichen Datentyp sind. Es sollte also möglich sein, erheblich effizientere
Programme zu schreiben, indem man Matrizen nicht durch Listen darstellt, sondern durch
einen auf diese Aufgabe zugeschnittenen Datentypen. Hierzu greift man auf das von NumPy
zur Verfügung gestellte ndarray-Objekt, also ein N-dimensionales Array, zurück.
NumPy-Arrays¶
Bevor wir mit NumPy-Arrays [1] arbeiten können, müssen wir NumPy importieren.
Da der Namensraum von NumPy sehr groß ist, empfiehlt es sich, diesen nicht mit
from numpy import * zu importieren. Auch der Import einzelner Objekte empfiehlt
sich nicht. Importiert man beispielsweise die Sinusfunktion aus NumPy, so ist
weiter unten in einem Pythonskript nicht mehr ohne Weiteres erkennbar, ob es sich
um den Sinus aus NumPy oder aus dem math-Modul handelt. Üblicherweise importiert
man daher NumPy in folgender Weise:
In [1]: import numpy as np
Die Abkürzung np erspart dabei etwas Schreibarbeit, macht aber zugleich die Herkunft
eines Objekts deutlich. Hält man sich an diese Konvention, so trägt man zur Verständlichkeit
des Codes bei.
Um die Eigenschaften von Arrays zu untersuchen, müssen wir zunächst wissen, wie sich ein
Array erzeugen lässt. Nachdem wir im vorigen Unterkapitel die Verwendung von
Listen für die Darstellung von Matrizen diskutiert haben, mag man versucht sein,
zu diesem Zweck die append-Methode von NumPy zu verwenden. Hiervon ist
allerdings abzuraten, da bei jeder Ausführung von append eine Kopie des
NumPy-Arrays erstellt wird. Vor allem bei großen Arrays kann bereits das Anlegen
einer Kopie im Speicher sehr zeitaufwendig sein, und dies gilt ganz besonders,
wenn dieser Kopiervorgang häufig durchgeführt werden muss. Bei der Arbeit mit
NumPy-Arrays wird man also nach Möglichkeit immer darauf achten, dass keine
unnötigen Kopien von Arrays angelegt werden. Für die Erzeugung von NumPy-Arrays
bedeutet dies, dass man am besten die Größe bereits zu Beginn festlegt und dann aus den
vielen zur Verfügung stehenden Methoden eine geeignete auswählt, um das Array
mit Werten zu füllen.
In NumPy ist es sehr einfach, die Dokumentation nach einem bestimmten Text zu durchsuchen. Die zahlreichen Möglichkeiten, ein Array zu erzeugen, lassen sich folgendermaßen erhalten:
In [2]: np.lookfor('create array')
Search results for 'create array'
---------------------------------
numpy.array
Create an array.
numpy.memmap
Create a memory-map to an array stored in a *binary* file on disk.
numpy.diagflat
Create a two-dimensional array with the flattened input as a diagonal.
numpy.fromiter
Create a new 1-dimensional array from an iterable object.
...
Dabei wurde hier nur ein Teil der Ausgabe dargestellt. Gleich der erste Eintrag verrät
uns, wie man aus einer Liste von Listen ein Array erzeugen kann. Details hierzu erhält
man bei Bedarf wie üblich mit help(np.array) oder alternativ mit
np.info(np.array).
In [3]: matrix = [[0, 1, 2],
...: [3, 4, 5],
...: [6, 7, 8]]
In [4]: myarray = np.array(matrix)
In [5]: myarray
Out[5]:
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
In [6]: type(myarray)
Out[6]: numpy.ndarray
Ein Array besitzt als wesentliche Bestandteile die Daten im eigentlichen Sinne, also die Werte der einzelnen Matrixelemente, sowie Information darüber, wie auf ein spezifisches Matrixelement zugegriffen werden kann. Die Daten sind im Speicher einfach hintereinander, also in eindimensionaler Form, abgelegt. Dabei gibt es die Möglichkeit, die Matrix zeilenweise oder spaltenweise abzuspeichern. Ersteres wird von der Programmiersprache C verwendet, während die zweite Variante von Fortran verwendet wird.
Nachdem die Daten strukturlos im Speicher abgelegt sind, müssen
ndarray-Objekte, wie schon erwähnt, neben den Daten auch Informationen
darüber besitzen, wie auf einzelne Matrixelemente zugegriffen wird. Auf diese
Weise lässt sich sehr leicht die Adresse der Daten eines Matrixelements
bestimmen. Zudem ist es möglich, die gleichen Daten im Speicher auf verschiedene
Weise anzusehen. Damit ist es häufig möglich, unnötige Kopiervorgänge im
Speicher zu vermeiden. Wie weiter oben schon angedeutet ist dies von großer
Bedeutung für die Effizienz des Programms. Aus diesem Grunde ist es wichtig zu
wissen, ob NumPy im Einzelfall nur eine andere Sicht auf die Daten zur Verfügung
stellt oder tatsächlich ein neues Array erzeugt.
Um die Informationen über die Struktur eines Arrays besser zu verstehen, definieren wir uns eine Funktion, die einige Attribute des Arrays ausgibt.
In [7]: def array_attributes(a):
...: for attr in ('ndim', 'size', 'itemsize', 'dtype', 'shape', 'strides'):
...: print('{:8s}: {}'.format(attr, getattr(a, attr)))
Zum Experimentieren mit Arrays ist die arange-Methode sehr praktisch, die
ähnlich wie das uns bereits bekannte range eine Reihe von Zahlen erzeugt,
nun jedoch in einem Array.
In [8]: matrix = np.arange(16)
In [9]: matrix
Out[9]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
In [10]: array_attributes(matrix)
ndim : 1
size : 16
itemsize: 8
dtype : int64
shape : (16,)
strides : (8,)
Das Attribut ndim gibt an, dass wir es mit einem eindimensionalen Array
zu tun haben, während das Attribut size anzeigt, dass das Array insgesamt
16 Elemente besitzt. Jedes Element besitzt den Datentyp (dtype) int64.
Es handelt sich also um 64-Bit-Integers, die eine Größe von 8 Byte (itemsize)
besitzen. Die Attribute können wir auch direkt in der üblichen objektorientierten
Schreibweise ansprechen. Zum Beispiel gibt
In [11]: matrix.nbytes
Out[11]: 128
den Speicherplatzbedarf des Arrays in Bytes an.
Für Arrays kommen eine ganze Reihe verschiedener Datentypen in Frage, zum Beispiel
Integers verschiedener Länge (int8, int16, int32, int64) oder
auch ohne Vorzeichen (uint8, …), Gleitkommazahlen (float16, float32,
float64), komplexe Zahlen (complex64, complex128), Wahrheitswerte
(bool8) und sogar Unicode-Strings als nichtnumerischer Datentyp. Wenn der
Datentyp nicht angegeben oder durch die Konstruktion des Arrays bestimmt ist,
werden die im jeweiligen System standardmäßig verwendeten Gleitkommazahlen
herangezogen, also meistens float64. Bei Integers ist zu beachten, dass
es im Gegensatz zu Python-Integers wegen der endlichen Länge zu einem Überlauf
kommen kann, wie das folgende Beispiel demonstriert.
In [12]: np.arange(1, 160, 10, dtype=np.int8)
Out[12]:
array([ 1, 11, 21, 31, 41, 51, 61, 71, 81, 91, 101,
111, 121, -125, -115, -105], dtype=int8)
 Wie kann man diese Ausgabe verstehen?
Wie kann man diese Ausgabe verstehen?
Besonders interessant sind die beiden Attribute shape und strides. Der
Wert des Attributs shape, in unserem Beispiel das Tupel (16,), gibt die
Zahl der Elemente in der jeweiligen Dimension an. Um dies besser zu verstehen,
ändern wir dieses Attribut ab, wobei darauf zu achten ist, dass die Zahl der
Elemente des Arrays erhalten bleibt. Wir wandeln das eindimensionale Array mit
16 Elementen in ein 4×4-Array um.
In [13]: matrix.shape = (4, 4)
In [14]: matrix
Out[14]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
In [15]: matrix.strides
Out[15]: (32, 8)
Dabei wird deutlich, dass nicht nur die Form (shape) modifiziert wurde, sondern
auch aus dem Tupel (8,) des Attributs strides [2] das Tupel (32, 8) wurde.
Die strides geben an, um wieviel Bytes man weitergehen muss, um zum nächsten Element
in dieser Dimension zu gelangen. Die folgende Abbildung zeigt dies an einem
kleinen Array.
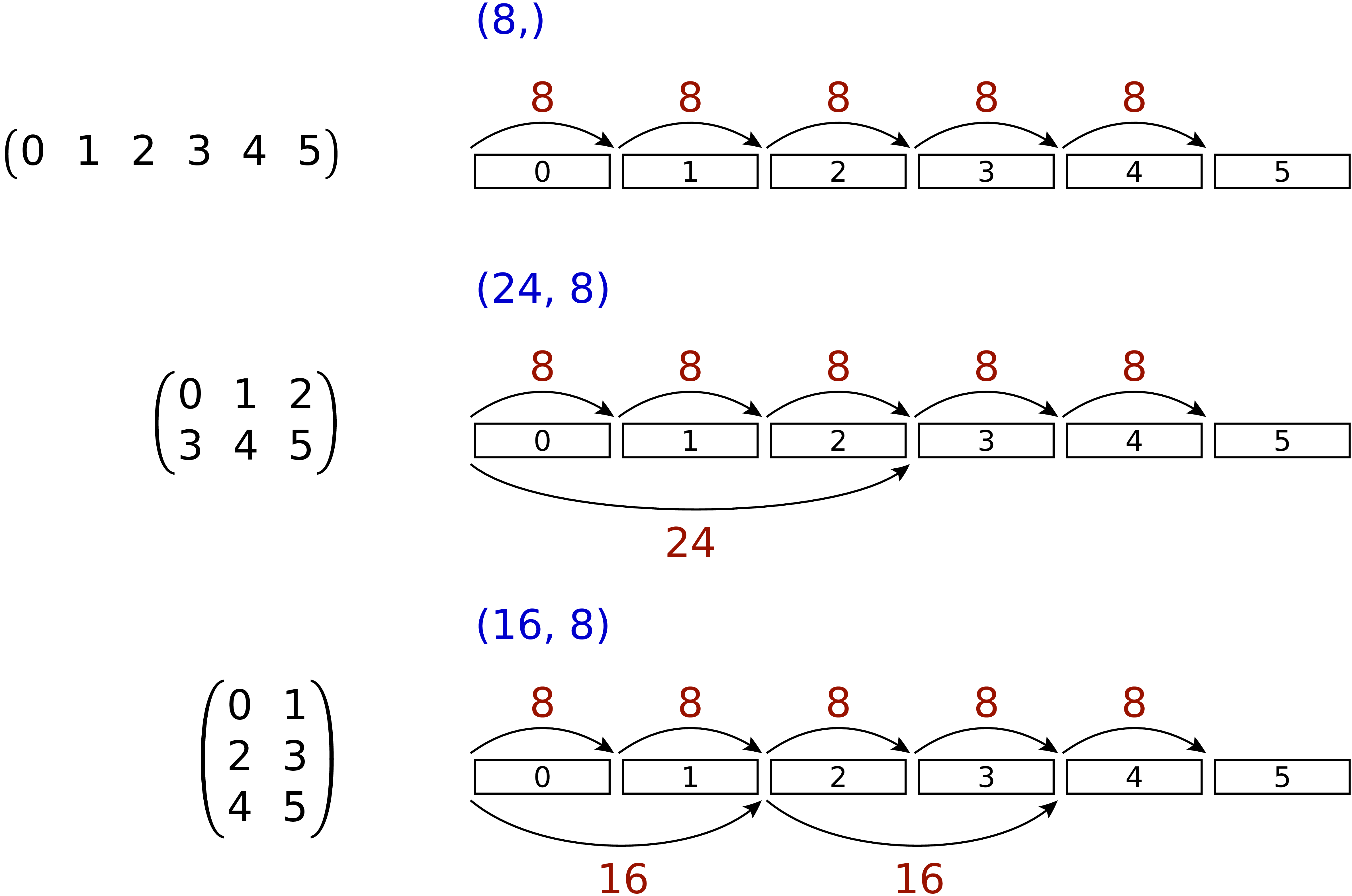
Greifen wir speziell den mittleren Fall mit den strides (24, 8) heraus.
Bewegt man sich in einer Zeile der Matrix von Element zu Element, so muss man
im Speicher jeweils um 8 Bytes weitergehen, wenn ein Datentyp int64
vorliegt. Entlang einer Spalte beträgt die Schrittweite dagegen 24 Bytes.
 Wie verändern sich die strides in dem 16-elementigen Array
Wie verändern sich die strides in dem 16-elementigen Array np.arange(16),
wenn man einen shape von (2, 2, 2, 2) wählt?
Für die Anwendung ist es wichtig zu wissen, dass die Manipulation der Attribute
shape und strides nicht die Daten im Speicher verändert. Es wird also
nur eine neue Sicht auf die vorhandenen Daten vermittelt. Dies ist insofern von
Bedeutung als das Kopieren von größeren Datenmengen durchaus mit einem nicht
unerheblichen Zeitaufwand verbunden sein kann.
Um uns davon zu überzeugen, dass tatsächlich kein neues Array erzeugt wird, generieren
wir nochmals ein eindimensionales Array und daraus mit Hilfe von reshape ein
zweidimensionales Array.
In [16]: m1 = np.arange(16)
In [17]: m1
Out[17]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
In [18]: m2 = m1.reshape(4, 4)
In [19]: m2
Out[19]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
Nun ändern wir das erste Element in dem eindimensionalen Array ab und stellen in der Tat fest, dass sich diese Änderung auch auf das zweidimensionale Array auswirkt.
In [20]: m1[0] = 99
In [21]: m1
Out[21]: array([99, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
In [22]: m2
Out[22]:
array([[99, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
Eine Matrix lässt sich auch transponieren, ohne dass Matrixelemente im Speicher hin und her kopiert werden müssen. Stattdessen werden nur die beiden Werte der strides vertauscht.
In [23]: m2.strides
Out[23]: (32, 8)
In [24]: m2.T
Out[24]:
array([[99, 4, 8, 12],
[ 1, 5, 9, 13],
[ 2, 6, 10, 14],
[ 3, 7, 11, 15]])
In [25]: m2.T.strides
Out[25]: (8, 32)
Obwohl die Daten im Speicher nicht verändert wurden, kann man jetzt mit der transponierten Matrix arbeiten.
Mit Hilfe der Attribute shape und strides lässt sich die Sicht auf ein
Array auf sehr flexible Weise festlegen. Allerdings ist der Benutzer selbst für
die Folgen verantwortlich, wie der zweite Teil des folgenden Beispiels zeigt.
Dazu gehen wir zu unserem ursprünglichen 4×4-Array zurück und verändern das
Attribut strides mit Hilfe der as_strided-Methode.
In [26]: matrix = np.arange(16).reshape(4, 4)
In [27]: matrix1 = np.lib.stride_tricks.as_strided(matrix, strides=(16, 16))
In [28]: matrix1
Out[28]:
array([[ 0, 2, 4, 6],
[ 2, 4, 6, 8],
[ 4, 6, 8, 10],
[ 6, 8, 10, 12]])
In [29]: matrix2 = np.lib.stride_tricks.as_strided(matrix, shape=(4, 4), strides=(16, 4))
In [30]: matrix2
Out[30]:
array([[ 0, 4294967296, 1, 8589934592],
[ 2, 12884901888, 3, 17179869184],
[ 4, 21474836480, 5, 25769803776],
[ 6, 30064771072, 7, 34359738368]])
Im ersten Fall ist der Wert der strides gerade das Doppelte der Datenbreite, so dass in einer Zeile von einem Wert zum nächsten jeweils ein Wert im Array übersprungen wird. Beim Übergang von einer Zeile zur nächsten wird gegenüber dem Beginn der vorherigen Zeile auch nur um zwei Werte vorangeschritten, so dass sich das gezeigte Resultat ergibt.
Im zweiten Beispiel wurde ein stride gewählt, der nur die Hälfte einer Datenbreite beträgt. Der berechnete Beginn eines neuen Werts im Speicher liegt damit nicht an einer Stelle, die einem tatsächlichen Beginn eines Werts entspricht. Python interpretiert dennoch die erhaltene Information und erzeugt so das obige Array. In unserem Beispiel erreicht man bei jedem zweiten Wert wieder eine korrekte Datengrenze. Die Manipulation von strides erfordert also eine gewisse Sorgfalt, und man ist für eventuelle Fehler selbst verantwortlich.
Erzeugung von NumPy-Arrays¶
NumPy-Arrays lassen sich je nach Bedarf auf verschiedene Arten erzeugen. Die
Basis bildet die ndarray-Methode, auf die man immer zurückgreifen kann.
In den meisten Fällen wird es aber praktischer sein, eine der spezialisierteren
Methoden zu verwenden, die wir im Folgenden besprechen wollen.
Um ein mit Nullen aufgefülltes 2×2-Array zu erzeugen, geht man folgendermaßen vor:
In [1]: matrix1 = np.zeros((2, 2))
In [2]: matrix1, matrix1.dtype
Out[2]:
(array([[ 0., 0.],
[ 0., 0.]]), dtype('float64'))
Das Tupel im Argument gibt dabei die Form des Arrays vor. Wird der Datentyp der Einträge nicht weiter spezifiziert, so werden Gleitkommazahlen mit einer Länge von 8 Bytes verwendet. Man kann aber auch explizit zum Beispiel Integereinträge verlangen:
In [3]: np.zeros((2, 2), dtype=np.int)
Out[3]:
array([[0, 0],
[0, 0]])
Neben der zeros-Funktion gibt es auch noch die empty-Funktion, die zwar
den benötigten Speicherplatz zur Verfügung stellt, diesen jedoch nicht initialisiert.
Im Allgemeinen werden also die Arrayelemente von den hier im Beispiel gezeigten
abweichen.
In [4]: np.empty((3, 3))
Out[4]:
array([[ 6.91153891e-310, 2.32617410e-316, 6.91153265e-310],
[ 6.91153265e-310, 6.91153265e-310, 6.91153265e-310],
[ 6.91153265e-310, 6.91153265e-310, 3.95252517e-322]])
Die empty-Funktion sollte also nur verwendet werden, wenn die Arrayelemente
später noch belegt werden.
Will man alle Elemente eines Arrays mit einem konstanten Wert ungleich Null
füllen, so kann man ones verwenden und das sich ergebende Array mit einem
Faktor multiplizieren.
In [5]: 2*np.ones((2, 3))
Out[5]:
array([[ 2., 2., 2.],
[ 2., 2., 2.]])
Häufig benötigt man eine Einheitsmatrix, die man mit Hilfe von identity
erhält:
In [6]: np.identity(3)
Out[6]:
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
Hierbei wird immer eine Diagonalmatrix erzeugt. Will man dies nicht, so kann
man eye verwenden, das nicht nur nicht quadratische Arrays erzeugen kann,
sondern auch die Diagonale nach oben oder unten verschieben lässt.
In [7]: np.eye(2, 4)
Out[7]:
array([[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.]])
Zu beachten ist hier, dass die Form des Arrays nicht als Tupel vorgegeben wird,
da ohnehin nur zweidimensionale Arrays erzeugt werden können. Lässt man das
zweite Argument weg, so wird ein quadratisches Array erzeugt. Will man die
Diagonaleinträge verschieben, so gibt man dies mit Hilfe des Parameters k an:
In [8]: np.eye(4, k=1)-np.eye(4, k=-1)
Out[8]:
array([[ 0., 1., 0., 0.],
[-1., 0., 1., 0.],
[ 0., -1., 0., 1.],
[ 0., 0., -1., 0.]])
Eine Diagonalmatrix mit unterschiedlichen Einträgen lässt sich aus einem eindimensionalen Array folgendermaßen erzeugen:
In [9]: np.diag([1, 2, 3, 4])
Out[9]:
array([[1, 0, 0, 0],
[0, 2, 0, 0],
[0, 0, 3, 0],
[0, 0, 0, 4]])
Dabei lässt sich wie bei der eye-Funktion die Diagonale verschieben.
In [10]: np.diag([1, 2, 3, 4], k=1)
Out[10]:
array([[0, 1, 0, 0, 0],
[0, 0, 2, 0, 0],
[0, 0, 0, 3, 0],
[0, 0, 0, 0, 4],
[0, 0, 0, 0, 0]])
Umgekehrt kann man mit der diag-Funktion auch die Diagonalelemente eines
zweidimensionalen Arrays extrahieren.
In [11]: matrix = np.arange(16).reshape(4, 4)
In [12]: matrix
Out[12]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
In [13]: np.diag(matrix)
Out[13]: array([ 0, 5, 10, 15])
Lassen sich die Arrayeinträge als Funktion der Indizes ausdrücken, so kann
man die fromfunction-Funktion verwenden, wie in dem folgenden Beispiel
zu sehen ist, das eine Multiplikationstabelle erzeugt.
In [14]: np.fromfunction(lambda i, j: (i+1)*(j+1), (6, 6), dtype=np.int)
Out[14]:
array([[ 1, 2, 3, 4, 5, 6],
[ 2, 4, 6, 8, 10, 12],
[ 3, 6, 9, 12, 15, 18],
[ 4, 8, 12, 16, 20, 24],
[ 5, 10, 15, 20, 25, 30],
[ 6, 12, 18, 24, 30, 36]])
Diese Funktion ist nicht auf zweidimensionale Arrays beschränkt.
Bei der Konstruktion von Arrays sind auch Funktionen interessant, die als
Verallgemeinerung der in Python eingebauten Funktion range angesehen werden
können. Ihr Nutzen ergibt sich vor allem aus der Tatsache, dass man gewissen
Funktionen, den universellen Funktionen oder ufuncs in NumPy, die wir im
Abschnitt Universelle Funktionen besprechen werden, ganze Arrays als Argumente übergeben
kann. Damit wird eine besonders effiziente Auswertung dieser Funktionen
möglich.
Eindimensionale Arrays lassen sich mit Hilfe von arange, linspace und
logspace erzeugen:
In [15]: np.arange(1, 2, 0.1)
Out[15]: array([ 1. , 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9])
Ähnlich wie bei range erzeugt arange aus der Angabe eines Start- und
eines Endwerts sowie einer Schrittweite eine Folge von Werten. Allerdings
können diese auch Gleitkommazahlen sein. Zudem wird statt einer Liste ein Array
erzeugt. Wie bei range ist der Endwert hierin nicht enthalten. Allerdings
können Rundungsfehler zu unerwarteten Effekten führen.
In [16]: np.arange(1, 1.5, 0.1)
Out[16]: array([ 1. , 1.1, 1.2, 1.3, 1.4])
In [17]: np.arange(1, 1.6, 0.1)
Out[17]: array([ 1. , 1.1, 1.2, 1.3, 1.4, 1.5, 1.6])
In [18]: np.arange(1, 1.601, 0.1)
Out[18]: array([ 1. , 1.1, 1.2, 1.3, 1.4, 1.5, 1.6])
Dieses Problem kann man umgehen, wenn man statt der Schrittweite eine Anzahl
von Punkten in dem gegebenen Intervall vorgibt. Dafür ist linspace eine
geeignete Funktion, sofern die Schrittweite konstant sein soll. Bei Bedarf kann
man sich neben dem Array auch noch die Schrittweite ausgeben lassen. Benötigt
man eine logarithmische Skala, so verwendet man logspace, das den
Exponenten linear zwischen einem Start- und einem Endwert verändert. Die Basis
ist standardmäßig 10, sie kann aber durch Setzen des Parameters base an
spezielle Erfordernisse angepasst werden.
In [19]: np.linspace(1, 2, 11)
Out[19]: array([ 1. , 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2. ])
In [20]: np.linspace(1, 2, 4, retstep=True)
Out[20]:
(array([ 1. , 1.33333333, 1.66666667, 2. ]),
0.3333333333333333)
In [21]: np.logspace(0, 3, 6)
Out[21]:
array([ 1. , 3.98107171, 15.84893192, 63.09573445,
251.18864315, 1000. ])
In [22]: np.logspace(0, 3, 4, base=2)
Out[22]: array([ 1., 2., 4., 8.])
Gerade bei der graphischen Darstellung von Funktionen sind linspace
und logspace besonders nützlich. Im folgenden Beispiel verwenden
wir die matplotlib-Bibliothek, die im Abschnitt Erstellung von Grafiken mit matplotlib besprochen wird.
In [23]: import matplotlib.pyplot as plt
In [24]: x = np.linspace(0, 2*np.pi)
In [25]: y = np.sin(x)
In [26]: plt.plot(x, y)
Out[26]: [<matplotlib.lines.Line2D at 0x7f3ad50b76a0>]

Möchte man eine Funktion auf einem Gitter auswerten und benötigt man dazu
separate Arrays für die x- und y-Werte, so hilft meshgrid weiter.
In [27]: xvals, yvals = np.meshgrid([-1, 0, 1], [2, 3, 4])
In [28]: xvals
Out[28]:
array([[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]])
In [29]: yvals
Out[29]:
array([[2, 2, 2],
[3, 3, 3],
[4, 4, 4]])
In diesem Zusammenhang sind auch die Funktionen mgrid und ogrid von
Interesse, die wir im Abschnitt Universelle Funktionen besprechen werden, nachdem wir die
Adressierung von Arrays genauer angesehen haben.
Zur graphischen Darstellung von Daten ist es häufig erforderlich, die Daten
zunächst aus einer Datei einzulesen und in einem Array zu speichern. Neben wir
an, wir hätten eine Datei x_von_t.dat mit folgendem Inhalt:
# Zeit Ort
0.0 0.0
0.1 0.1
0.2 0.4
0.3 0.9
Hierbei zeigt das #-Zeichen in der ersten Zeile an, dass es sich um eine
Kommentarzeile handelt, die nicht in das Array übernommen werden soll. Unter
Verwendung von loadtxt kann man die Daten nun einlesen:
In [30]: np.loadtxt("x_von_t.dat")
Out[30]:
array([[ 0. , 0. ],
[ 0.1, 0.1],
[ 0.2, 0.4],
[ 0.3, 0.9]])
Bei der loadtxt-Funktion lassen sich zum Beispiel das Kommentarzeichen oder
die Trennzeichen zwischen Einträgen konfigurieren. Noch wesentlich flexibler
ist genfromtxt, das es unter anderem erlaubt, Spaltenüberschriften aus der
Datei zu entnehmen oder mit fehlenden Einträgen umzugehen. Für Details wird auf
die zugehörige Dokumentation
verwiesen.
Abschließend betrachten wir noch kurz die Erzeugung von Zufallszahlen, die man zum Beispiel für Simulationszwecke benötigt. Statt viele einzelne Zufallszahlen zu erzeugen ist es häufig effizienter, gleich ein ganzes Array mit Zufallszahlen zu füllen. Im folgenden Beispiel erzeugen wir ein Array mit zehn im Intervall zwischen 0 und 1 gleich verteilten Pseudozufallszahlen. Reproduzierbar werden die Zahlenwerte, wenn zunächst ein Startwert für die Berechnung, ein seed, gesetzt wird.
In [31]: np.random.rand(2, 5)
Out[31]:
array([[ 0.99281469, 0.90376223, 0.81096671, 0.33726814, 0.34463236],
[ 0.74234766, 0.05862623, 0.49005243, 0.73496906, 0.21421244]])
In [32]: np.random.rand(2, 5)
Out[32]:
array([[ 0.51071925, 0.11952145, 0.12714712, 0.98081263, 0.05736099],
[ 0.35101524, 0.86407263, 0.80264858, 0.36629556, 0.59562485]])
In [33]: np.random.seed(1234)
In [34]: np.random.rand(2, 5)
Out[34]:
array([[ 0.19151945, 0.62210877, 0.43772774, 0.78535858, 0.77997581],
[ 0.27259261, 0.27646426, 0.80187218, 0.95813935, 0.87593263]])
In [35]: np.random.rand(2, 5)
Out[35]:
array([[ 0.19151945, 0.62210877, 0.43772774, 0.78535858, 0.77997581],
[ 0.27259261, 0.27646426, 0.80187218, 0.95813935, 0.87593263]])
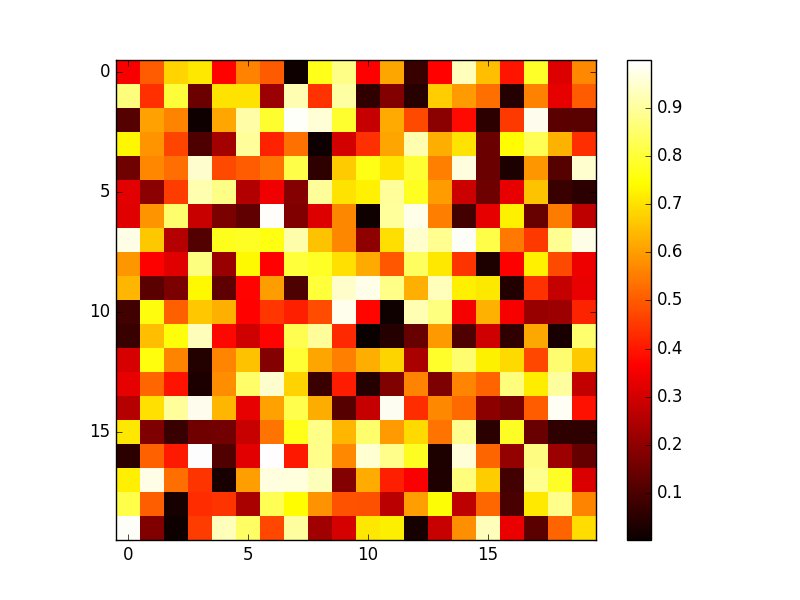
Die Zufälligkeit der Daten lässt sich graphisch darstellen.
In [36]: data = np.random.rand(20, 20)
In [37]: plt.imshow(data, cmap=plt.cm.hot, interpolation='none')
Out[37]: <matplotlib.image.AxesImage at 0x7f4eacf147b8>
In [38]: plt.colorbar()
Out[38]: <matplotlib.colorbar.Colorbar at 0x7f4eac6a60f0>
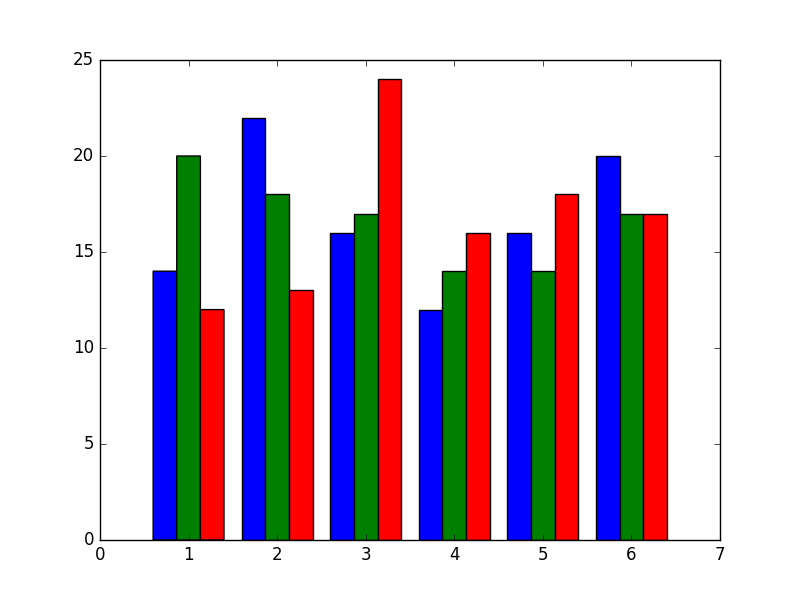
Als Anwendung betrachten wir drei Realisierungen von hundert Würfen eines
Würfels. Dazu erzeugen wir mit randint(1, 7) ganzzahlige Pseudozufallszahlen
zwischen 1 und 6 in einem zweidimensionalen Array der Form (100, 3). Diese
drei Spalten zu je 100 Zahlen werden jeweils als Histogramm dargestellt.
In [14]: wuerfe = np.random.randint(1, 7, (100, 3))
In [15]: plt.hist(wuerfe, np.linspace(0.5, 6.5, 7))
Out[15]:
([array([ 14., 22., 16., 12., 16., 20.]),
array([ 20., 18., 17., 14., 14., 17.]),
array([ 12., 13., 24., 16., 18., 17.])],
array([ 0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5]),
<a list of 3 Lists of Patches objects>)
Adressierung von NumPy-Arrays¶
Die Adressierungsmöglichkeiten für NumPy-Arrays basieren auf der so genannten
slice-Syntax, die wir von Python-Listen her kennen und uns hier noch einmal
kurz in Erinnerung rufen wollen. Einen Ausschnitt aus einer Liste, ein slice,
erhält man durch die Notation [start:stop:step]. Hierbei werden ausgehend
von dem Element mit dem Index start die Elemente bis vor das Element mit dem
Index stop mit einer Schrittweite step ausgewählt. Wird die Schrittweite
nicht angegeben, so nimmt step den Defaultwert 1 an. Negative Schrittweiten
führen in der Liste von hinten nach vorne. Fehlen start und/oder
stop so beginnen die ausgewählten Elemente mit dem ersten Element bzw. enden
mit dem letzten Element. Negative Indexwerte werden vom Ende der Liste her genommen.
Das letzte Element kann also mit dem Index -1, das vorletzten Element mit
dem Index -2 usw. angesprochen werden. Diese Indizierung funktioniert so auch
für NumPy-Arrays wie die folgenden Beispiele zeigen.
In [1]: a = np.arange(10)
In [2]: a
Out[2]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [3]: a[:]
Out[3]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [4]: a[::2]
Out[4]: array([0, 2, 4, 6, 8])
In [5]: a[1:4]
Out[5]: array([1, 2, 3])
In [6]: a[6:-2]
Out[6]: array([6, 7])
In [7]: a[::-1]
Out[7]: array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
Für mehrdimensionale Arrays wird die Notation direkt verallgemeinert. Im Gegensatz zu der im Abschnitt Python-Listen und Matrizen beschriebenen Notation für Listen von Listen werden hier die diversen Indexangaben durch Kommas getrennt zusammengefasst. Einige Beispiele für zweidimensionale Arrays sollen das illustrieren.
In [8]: a = np.arange(36).reshape(6, 6)
In [9]: a
Out[9]:
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29],
[30, 31, 32, 33, 34, 35]])
In [10]: a[:, :]
Out[10]:
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29],
[30, 31, 32, 33, 34, 35]])
In [11]: a[2:4, 2:4]
Out[11]:
array([[14, 15],
[20, 21]])
In [12]: a[2:4, 3:5]
Out[12]:
array([[15, 16],
[21, 22]])
In [13]: a[::2, ::2]
Out[13]:
array([[ 0, 2, 4],
[12, 14, 16],
[24, 26, 28]])
In [14]: a[2::2, ::2]
Out[14]:
array([[12, 14, 16],
[24, 26, 28]])
In [15]: a[2:4]
Out[15]:
array([[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])
Wie das letzte Beispiel zeigt, ergänzt NumPy bei fehlenden Indexangaben jeweils einen Doppelpunkt, so dass alle Elemente ausgewählt werden, die mit den explizit gemachten Indexangaben konsistent sind.
Will man eine Spalte (oder auch eine Zeile) in einer zweidimensionalen Array auswählen, so hat man zwei verschiedene Möglichkeiten:
In [16]: a[:, 0:1]
Out[16]:
array([[ 0],
[ 6],
[12],
[18],
[24],
[30]])
In [17]: a[:, 0]
Out[17]: array([ 0, 6, 12, 18, 24, 30])
Im ersten Fall sorgt die für beide Dimensionen vorhandene Indexnotation dafür, dass ein zweidimensionales Array erzeugt wird, das die Elemente der ersten Spalte enthält. Im zweiten Fall wird für die zweite Dimension ein fester Index angegeben, so dass nun ein eindimensionales Array erzeugt wird, die wiederum aus den Elementen der ersten Spalte besteht.
In einigen NumPy-Methoden gibt es einen Parameter axis, der die Richtung
in dem Array angibt, in der die Methode ausgeführt werden soll. Die Achsennummer
ergibt sich aus der Position der zugehörigen Indexangabe. Wie man aus den obigen
Beispielen entnehmen kann, verläuft die Achse 0 von oben nach unten, während die
Achse 1 von links nach rechts verläuft. Dies wird auch durch die folgende
Abbildung veranschaulicht.

Das Aufsummieren von Elementen unserer Beispielmatrix erfolgt dann mit Hilfe
der sum-Methode entweder von oben nach unten, von links nach rechts oder
über alle Elemente.
In [18]: a.sum(axis=0)
Out[18]: array([ 90, 96, 102, 108, 114, 120])
In [19]: a.sum(axis=1)
Out[19]: array([ 15, 51, 87, 123, 159, 195])
In [20]: a.sum()
Out[20]: 630
Zur Verdeutlichung betrachten wir noch ein dreidimensionales Array das im Folgenden graphisch dargestellt ist.
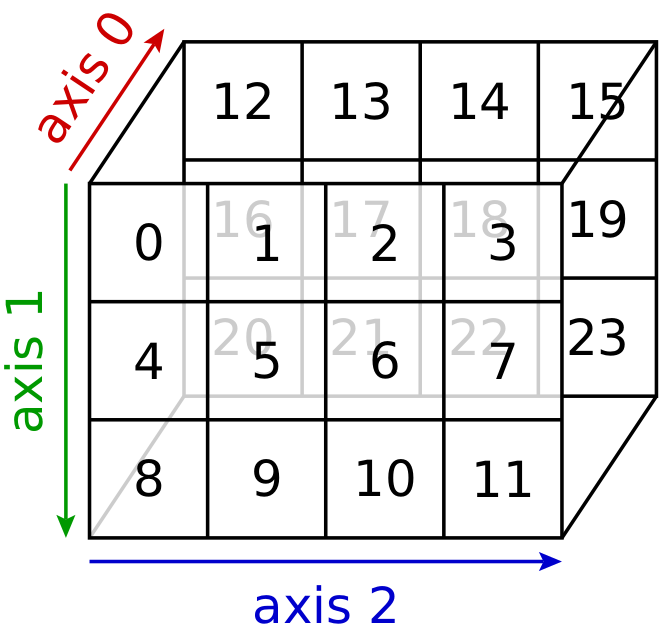
In [21]: b = np.arange(24).reshape(2, 3, 4)
In [22]: b
Out[22]:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
In [23]: b[0:1]
Out[23]:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]]])
In [24]: b[:, 0:1]
Out[24]:
array([[[ 0, 1, 2, 3]],
[[12, 13, 14, 15]]])
In [25]: b[:, :, 0:1]
Out[25]:
array([[[ 0],
[ 4],
[ 8]],
[[12],
[16],
[20]]])
In [26]: b[..., 0:1]
Out[26]:
array([[[ 0],
[ 4],
[ 8]],
[[12],
[16],
[20]]])
Man sieht hier deutlich, wie je nach Wahl der Achse ein entsprechender Schnitt
durch das als Würfel vorstellbare Array gemacht wird. Das letzte Beispiel zeigt
die Benutzung des Auslassungszeichens ... (im Englischen ellipsis genannt).
Es steht für die Anzahl von Doppelpunkten, die nötig sind, um die Indizes für
alle Dimensionen zu spezifizieren. Allerdings funktioniert dies nur beim ersten
Auftreten des Auslassungszeichens, da sonst nicht klar ist, wie viele Indexspezifikation
für jedes Auslassungszeichen einzusetzen sind. Alle weiteren Auslassungszeichen
werden daher durch einen einzelnen Doppelpunkt ersetzt.
Weiter oben hatten wir in einem Beispiel gesehen, dass die Angabe eines festen
Index die Dimension des Arrays effektiv um Eins vermindert. Umgekehrt ist es
auch möglich, eine zusätzliche Dimension der Länge Eins hinzuzufügen. Hierzu
dient newaxis, das an der gewünschten Stelle als Index eingesetzt werden kann.
Die folgenden Beispiele zeigen, wie aus einem eindimensionalen Array so zwei
verschiedene zweidimensionale Arrays konstruiert werden können.
In [27]: c = np.arange(5)
In [28]: c
Out[28]: array([0, 1, 2, 3, 4])
In [29]: c[:, np.newaxis]
Out[29]:
array([[0],
[1],
[2],
[3],
[4]])
In [30]: c[np.newaxis, :]
Out[30]: array([[0, 1, 2, 3, 4]])
Eine Anwendung hiervon werden wir weiter unten in diesem Kapitel kennenlernen, wenn wir uns mit der Erweiterung von Arrays auf eine Zielgröße, dem so genannten broadcasting beschäftigen.
Zunächst wollen wir aber noch eine weitere Indizierungsmethode, das so genannte fancy indexing, ansprechen. Obwohl es sich hierbei um ein sehr flexibles und mächtiges Verfahren handelt, sollte man bedenken, dass hier immer eine Kopie des Arrays erzeugt wird und nicht einfach nur eine neue Sicht auf bereits vorhandene Daten. Da Letzteres effizienter ist, sollte man fancy indexing in erster Linie in Situationen einsetzen, in denen das normale Indizieren nicht ausreicht.
Beim fancy indexing werden die möglichen Indizes als Arrays oder zum Beispiel als Liste, nicht jedoch als Tupel, angegeben. Die Elemente können dabei Integer oder Boolean sein. Beginnen wir mit dem ersten Fall, wobei wir zunächst von einem eindimensionalen Array ausgehen.
In [31]: a = np.arange(10, 20)
In [32]: a[[0, 3, 0, 5]]
Out[32]: array([10, 13, 10, 15])
In [33]: a[np.array([[0, 2], [1, 4]])]
Out[33]:
array([[10, 12],
[11, 14]])
Im ersten Fall werden einzelne Arrayelemente durch Angabe der Indizes ausgewählt, wobei auch Wiederholungen sowie eine nichtmonotone Wahl von Indizes möglich sind. Sind die Indizes als Array angegeben, so wird ein Array der gleichen Form erzeugt.
Bei der Auswahl von Elementen aus einem mehrdimensionalen Arrays muss man gegebenenfalls weitere Indexlisten oder -arrays angeben.
In [34]: a = np.arange(16).reshape(4, 4)
In [35]: a
Out[35]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
In [36]: a[[0, 1, 2]]
Out[36]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
In [37]: a[[0, 1, 2], [1, 2, 3]]
Out[37]: array([ 1, 6, 11])
Interessant ist die Verwendung von Indexarrays mit Elementen vom Typ Boolean. Ein solches Indexarray lässt sich zum Beispiel mit Hilfe einer logischen Operation auf einem Array erzeugen, wie das folgende Beispiel demonstriert. Eine Reihe von Zufallszahlen soll dabei bei einem Schwellenwert nach unten abgeschnitten werden.
1threshold = 0.3
2a = np.random.random(12)
3print a
4print "-"*30
5indexarray = a < threshold
6print indexarray
7print "-"*30
8a[indexarray] = threshold
9print a
Damit ergibt sich beispielsweise die folgende Ausgabe:
[ 0.11859559 0.49034494 0.08552061 0.69204077 0.18406457 0.06819091
0.36785529 0.16873423 0.44615435 0.57774615 0.54327126 0.57381642]
------------------------------
[ True False True False True True False True False False False False]
------------------------------
[ 0.3 0.49034494 0.3 0.69204077 0.3 0.3
0.36785529 0.3 0.44615435 0.57774615 0.54327126 0.57381642]
In Zeile 5 wird ein Array indexarray erzeugt, das an den Stellen, an denen die Elemente
des Arrays a kleiner als der Schwellwert sind, den Wahrheitswert True
besitzt. In Zeile 8 werden die auf diese Weise indizierten Elemente dann auf
den Schwellwert gesetzt. Es sei noch angemerkt, dass sich diese Funktionalität
auch direkt mit der clip-Funktion erreichen lässt.
Als Anwendungsbeispiel für die Indizierung von Arrays durch slicing und durch fancy indexing betrachten wir das Sieb des Eratosthenes zur Bestimmung von Primzahlen. Die folgende Abbildung illustriert das Prinzip.
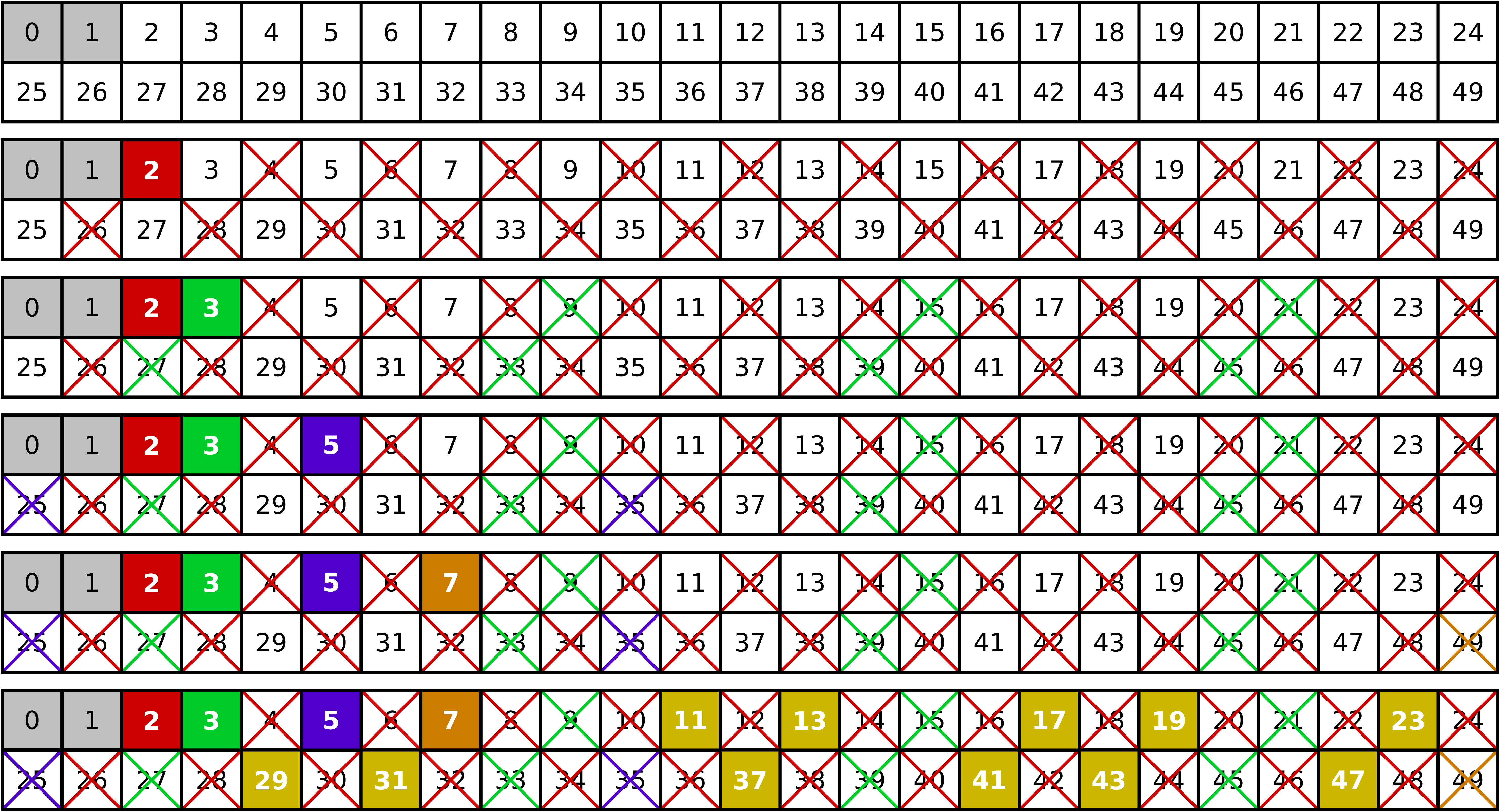
Ausgehend von der Zwei als kleinster Primzahl werden in aufsteigender Reihenfolge für alle Primzahlen deren Vielfache als Nichtprimzahlen identifiziert. Dies ist in der Abbildung durch Kreuze in der entsprechenden Farbe angedeutet. Beim Durchstreichen genügt es, mit dem Quadrat der jeweiligen Primzahl zu beginnen, da kleinere Vielfache bereits bei der Betrachtung einer kleineren Primzahl berücksichtigt wurden. So werden nacheinander alle Zahlen in der Liste identifiziert, die keine Primzahlen sind. Übrig bleiben somit die gesuchten Primzahlen. Eine Realisierung dieses Verfahrens unter Verwendung der Möglichkeiten von NumPy könnte folgendermaßen aussehen.
1nmax = 50
2integers = np.arange(nmax)
3is_prime = np.ones(nmax, dtype=bool)
4is_prime[:2] = False
5for j in range(2, int(np.sqrt(nmax))+1):
6 if is_prime[j]:
7 is_prime[j*j::j] = False
8print(integers[is_prime])
Als Ergebnis wird am Ende die Liste
[ 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47]
ausgegeben. Um die Indizierung leicht nachvollziehbar zu machen, enthält das
Array integers der zu untersuchenden Zahlen auch die Null und die Eins.
Nachdem in Zeile 3 zunächst alle Zahlen als potentielle Primzahlen markiert
werden, wird dies in Zeile 4 für die Null und die Eins gleich wieder rückgängig
gemacht. Da das Wegstreichen von Zahlen erst mit dem Quadrat einer Primzahl
beginnt, müssen nur Primzahlen bis zur Wurzel aus der maximalen Zahl nmax
betrachtet werden. In der Schleife der Zeilen 6 und 7 werden für jede dieser
Primzahlen beginnend bei deren Quadrat die Vielfachen der Primzahl bis zum Ende
der Liste zu Nichtprimzahlen erklärt. Die Ausgabe in Zeile 8 benutzt dann fancy
indexing mit Hilfe des booleschen Arrays is_prime, um die tatsächlichen
Primzahlen aus der Liste der potentiellen Primzahlen integers auszuwählen.
In einem Beispiel zum fancy indexing haben wir in der Vergleichsoperation a
< threshold ein Array (a) und ein Skalar (threshold) miteinander
verglichen. Wie kann dies funktionieren? Den Vergleich zweier Arrays derselben
Form kann man sinnvoll elementweise definieren. Soll ein Array mit einem Skalar
verglichen werden, so wird der Skalar von NumPy zunächst mit gleichen Elementen
so erweitert, das ein Array mit der benötigten Form entsteht. Dieser als
broadcasting bezeichnete Prozess kommt beispielsweise auch bei arithmetischen
Operationen zum Einsatz. Die beiden folgenden Anweisungen sind daher äquivalent:
In [38]: a = np.arange(5)
In [39]: a*3
Out[39]: array([ 0, 3, 6, 9, 12])
In [40]: a*np.array([3, 3, 3, 3, 3])
Out[40]: array([ 0, 3, 6, 9, 12])
Broadcasting ist genau dann möglich, wenn beim Vergleich der Achsen der beiden beteiligten Arrays von der letzten Achse beginnend die Länge der Achsen jeweils gleich ist oder eine Achse die Länge Eins besitzt. Eine Achse der Länge Eins wird durch Wiederholen der Elemente im erforderlichen Umfang verlängert. Entsprechendes geschieht beim Hinzufügen von Achsen von vorne, um die Dimensionen der Arrays identisch zu machen. Die folgende Abbildung illustriert das broadcasting.
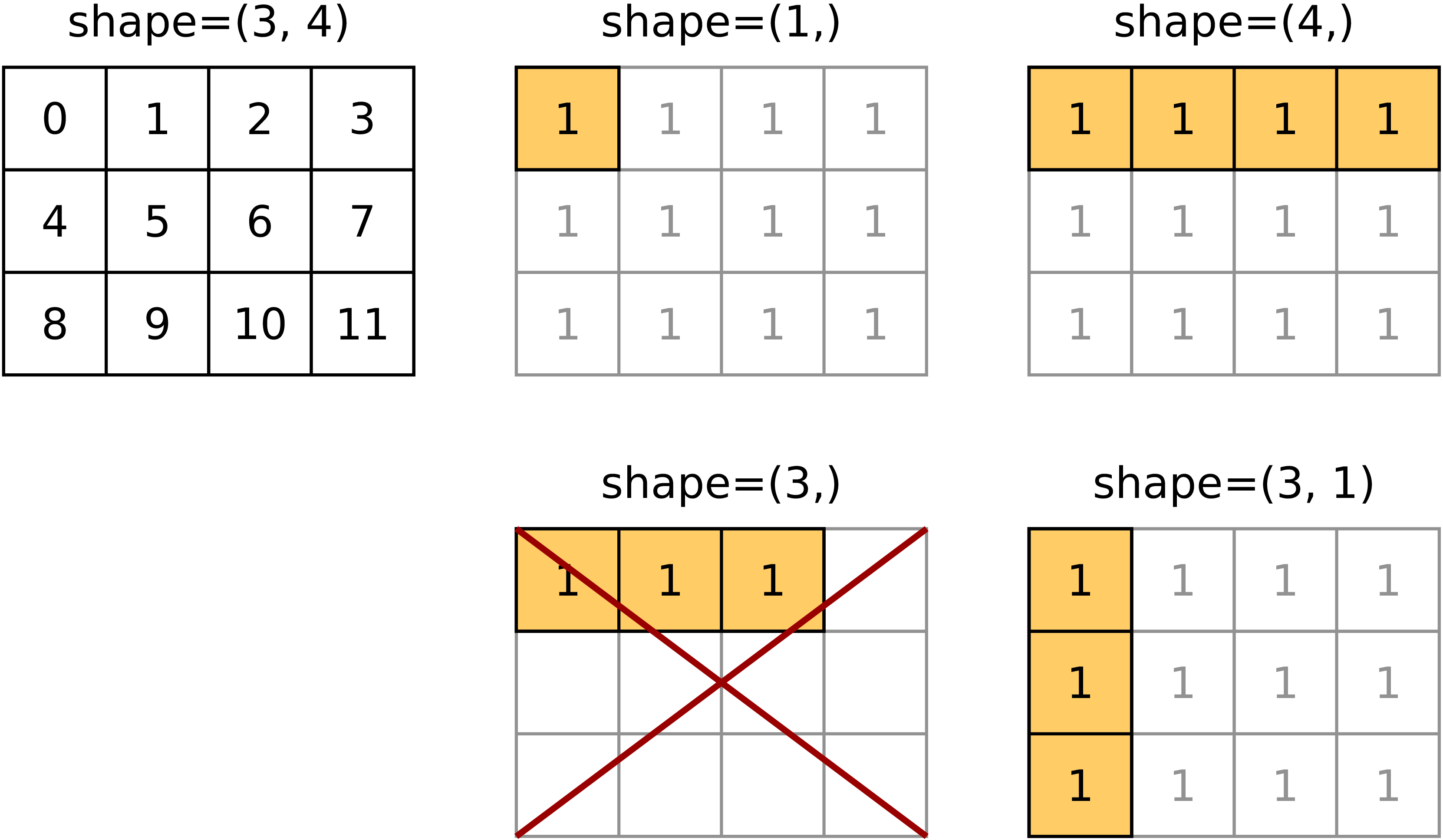
Hier ist ein Array der Form (3, 4) vorgegeben. Für ein Array der Form
(1,) wird die Länge auf die Länge der Achse 1 des ersten Array, also 4,
erweitert. Zudem wird eine weitere Achse 0 mit der gleichen Länge wie im
ursprünglichen Array hinzugefügt. Geht man von einem Array der Form (4,)
aus, so muss nur noch in gleicher Weise die Achse 0 hinzugefügt werden. Dagegen
genügt ein Array der Form (3,) nicht den Bedingungen des broadcasting, da
die Achse weder die Länge Eins noch die Länge der Achse 1 des ursprünglichen
Arrays besitzt. Anders ist dies bei einem Array der Form (3, 1), bei dem nur
die Länge der Achse 1 auf 4 erhöht werden muss.
Betrachten wir abschließend noch entsprechende Codebeispiele.
In [41]: a = np.arange(12.).reshape(3, 4)
In [42]: a
Out[42]:
array([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]])
In [43]: a+1.
Out[43]:
array([[ 1., 2., 3., 4.],
[ 5., 6., 7., 8.],
[ 9., 10., 11., 12.]])
In [44]: a+np.ones(4)
Out[44]:
array([[ 1., 2., 3., 4.],
[ 5., 6., 7., 8.],
[ 9., 10., 11., 12.]])
In [45]: a+np.ones(3)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-7-1b5c4daa3b16> in <module>()
----> 1 a+np.ones(3)
ValueError: operands could not be broadcast together with shapes (3,4) (3,)
In [46]: a+np.ones(3)[:, np.newaxis]
Out[46]:
array([[ 1., 2., 3., 4.],
[ 5., 6., 7., 8.],
[ 9., 10., 11., 12.]])
In [47]: a+np.ones(3).reshape(3, 1)
Out[47]:
array([[ 1., 2., 3., 4.],
[ 5., 6., 7., 8.],
[ 9., 10., 11., 12.]])
Universelle Funktionen¶
Im Abschnitt Erzeugung von NumPy-Arrays hatten wir in einem Beispiel bereits eine
Funktion auf ein Array angewandt. Um dieses Vorgehen besser zu verstehen,
importieren wir zusätzlich zum numpy-Paket, das in diesem Kapitel immer
importiert sein sollte, noch das math-Modul und versuchen dann, den Sinus
eines Arrays auszuwerten.
In [1]: import math
In [2]: math.sin(np.linspace(0, math.pi, 11))
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython console> in <module>()
TypeError: only length-1 arrays can be converted to Python scalars
Dabei scheitern wir jedoch, da der Sinus aus dem math-Modul nur mit skalaren Größen
umgehen kann. Hätte unser Array nur ein Element enthalten, so wären wir noch erfolgreich
gewesen. Im Beispiel hatten wir jedoch mehr als ein Element, genauer gesagt elf Elemente,
und somit kommt es zu einer TypeError-Ausnahme.
Den Ausweg bietet in diesem Fall das numpy-Paket selbst, das neben einer ganzen
Reihe weiterer Funktionen auch eine eigene Sinusfunktion zur Verfügung stellt. Diese ist
in der Lage, mit Arrays beliebiger Dimension umzugehen. Dabei wird die Funktion
elementweise angewandt und wieder ein Array der ursprünglichen Form erzeugt.
In [3]: np.sin(np.linspace(0, math.pi, 11))
Out[3]:
array([ 0.00000000e+00, 3.09016994e-01, 5.87785252e-01,
8.09016994e-01, 9.51056516e-01, 1.00000000e+00,
9.51056516e-01, 8.09016994e-01, 5.87785252e-01,
3.09016994e-01, 1.22460635e-16])
In [4]: np.sin(math.pi/6*np.arange(12).reshape(2, 6))
Out[4]:
array([[ 0.00000000e+00, 5.00000000e-01, 8.66025404e-01,
1.00000000e+00, 8.66025404e-01, 5.00000000e-01],
[ 1.22460635e-16, -5.00000000e-01, -8.66025404e-01,
-1.00000000e+00, -8.66025404e-01, -5.00000000e-01]])
Statt die Kreiszahl aus dem math-Modul zu nehmen, hätten wir sie genauso gut aus dem
numpy-Paket nehmen können.
Funktionen wie die gerade benutzte Sinusfunktion aus dem numpy-Paket, die
Arrays als Argumente akzeptieren, werden universelle Funktionen (universal
function oder kurz ufunc) genannt. Die im numpy-Paket verfügbaren
universellen Funktionen sind in der NumPy-Dokumentation zu ufuncs
aufgeführt. Implementationen von speziellen Funktionen als universelle Funktion
sind im scipy-Paket zu finden. Viele Funktionen in scipy.special,
jedoch nicht alle, sind als ufuncs implementiert. Als nur eines von vielen
möglichen Beispielen wählen wir die Gammafunktion:
In [5]: import scipy.special
In [6]: scipy.special.gamma(np.linspace(1, 5, 9))
Out[6]:
array([ 1. , 0.88622693, 1. , 1.32934039,
2. , 3.32335097, 6. , 11.6317284 , 24. ])
Gelegentlich benötigt man eine Funktion von zwei Variablen auf einem Gitter.
Man könnte hierzu die meshgrid-Funktion heranziehen, die wir im Abschnitt
Erzeugung von NumPy-Arrays erwähnt hatten. Dabei muss allerdings entweder die
Gitterpunkte explizit angeben oder beispielsweise mit linspace erzeugen.
Dann ist es häufig einfacher, ein mgrid-Gitter zu verwenden.
In [7]: np.mgrid[0:3, 0:3]
Out[7]:
array([[[0, 0, 0],
[1, 1, 1],
[2, 2, 2]],
[[0, 1, 2],
[0, 1, 2],
[0, 1, 2]]])
In [8]: np.mgrid[0:3:7j, 0:3:7j]
Out[8]:
array([[[ 0. , 0. , 0. , 0. , 0. , 0. , 0. ],
[ 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5],
[ 1. , 1. , 1. , 1. , 1. , 1. , 1. ],
[ 1.5, 1.5, 1.5, 1.5, 1.5, 1.5, 1.5],
[ 2. , 2. , 2. , 2. , 2. , 2. , 2. ],
[ 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5],
[ 3. , 3. , 3. , 3. , 3. , 3. , 3. ]],
[[ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. ],
[ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. ],
[ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. ],
[ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. ],
[ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. ],
[ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. ],
[ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. ]]])
Man beachte, dass im zweiten Fall das dritte Element in der slice-Syntax imaginär ist. Damit wird
angedeutet, dass nicht die Schrittweite gemeint ist, sondern die Anzahl der Werte im durch die
ersten beiden Zahlen spezifizierten Intervall. Das folgende Beispiel zeigt eine
weitere Anwendung. Man sieht hier, dass die Schrittweite in mgrid auch durch
eine Gleitkommazahl gegeben sein kann.
In [9]: x, y = np.mgrid[-10:10:0.1, -10:10:0.1]
In [10]: plt.imshow(np.sin(x*y))
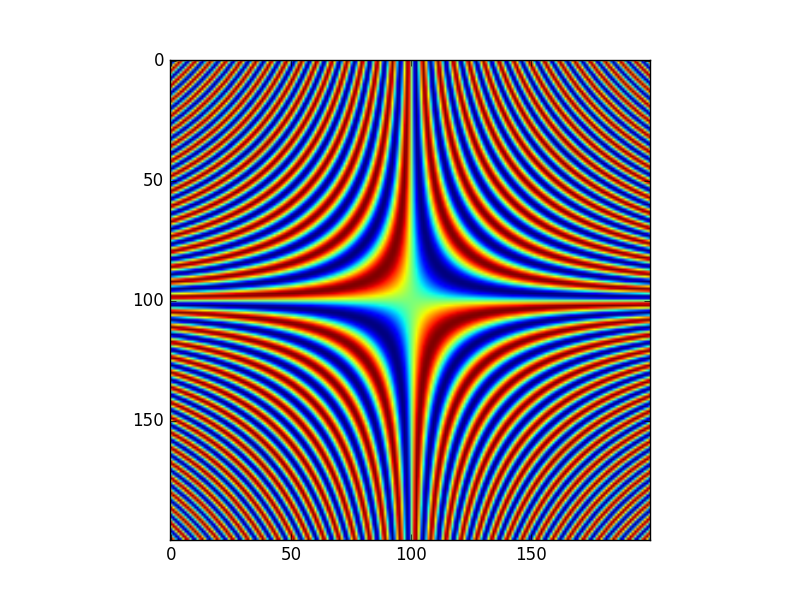
Unter Verwendung des broadcasting genügt auch ein mit ogrid erzeugtes Gitter,
das wesentlich weniger Speicherplatz erfordert.
In [11]: np.ogrid[0:3:7j, 0:3:7j]
Out[11]:
[array([[ 0. ],
[ 0.5],
[ 1. ],
[ 1.5],
[ 2. ],
[ 2.5],
[ 3. ]]),
array([[ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. ]])]
Alternativ kann man die Werte für x und y auch expliziter wie folgt
erzeugen.
In [12]: x = np.linspace(-40, 40, 200)
In [13]: y = x[:, np.newaxis]
In [14]: z = np.sin(np.hypot(x-10, y))+np.sin(np.hypot(x+10, y))
In [15]: plt.imshow(z, cmap='viridis')
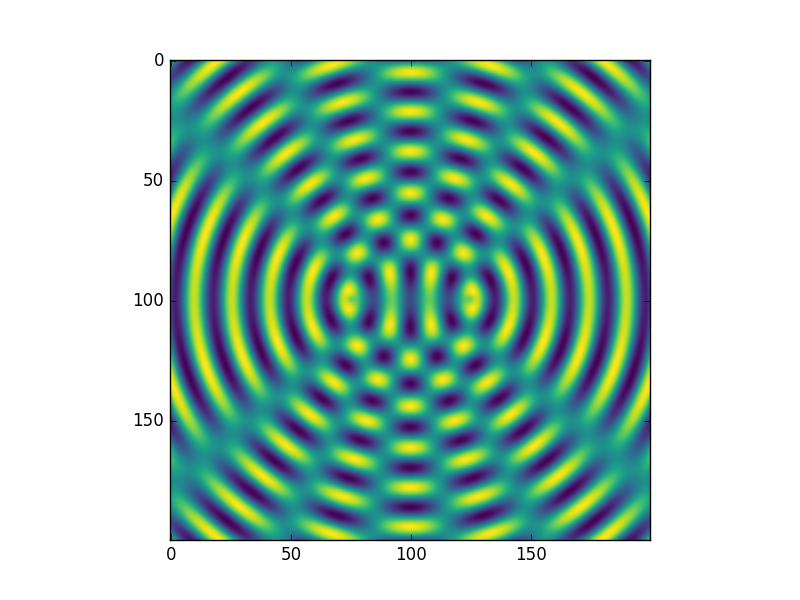
In Eingabe 13 ist es wichtig, dass eine weitere Achse hinzugefügt wird. Erst
dann spannen x und y durch broadcasting ein zweidimensionales Gitter
auf. In Eingabe 14 berechnet hypot die Länge der Hypotenuse eines
rechtwinkligen Dreiecks mit den durch die Argumente gegebenen Kathetenlängen.
Es ist nicht nur praktisch, Funktionen von Arrays direkt berechnen zu können, sondern es spart häufig auch Rechenzeit. Wir wollen dies an einem Beispiel illustrieren, in dem wir den Sinus entweder einzeln in einer Schleife oder mit Hilfe einer universellen Funktion berechnen.
1import math
2import matplotlib.pyplot as plt
3import numpy as np
4import time
5
6def sin_math(nmax):
7 xvals = np.linspace(0, 2*np.pi, nmax)
8 start = time.time()
9 for x in xvals:
10 y = math.sin(x)
11 return time.time()-start
12
13def sin_numpy(nmax):
14 xvals = np.linspace(0, 2*np.pi, nmax)
15 start = time.time()
16 yvals = np.sin(xvals)
17 return time.time()-start
18
19maxpower = 27
20nvals = np.empty(maxpower)
21tvals = np.empty_like(nvals)
22for nr, nmax in enumerate(np.logspace(1, maxpower, maxpower, base=2)):
23 nvals[nr] = nmax
24 tvals[nr] = sin_math(nmax)/sin_numpy(nmax)
25plt.rc('text', usetex=True)
26plt.xscale('log')
27plt.xlabel('$n_\mathrm{max}$', fontsize=20)
28plt.ylabel('$t_\mathrm{math}/t_\mathrm{numpy}$', fontsize=20)
29plt.plot(nvals, tvals, 'o')
30plt.show()
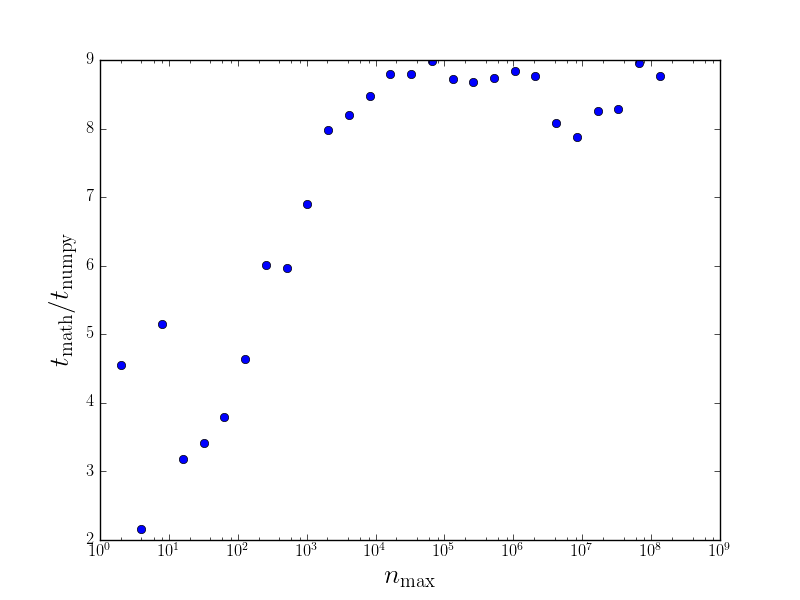
Ist die jeweilige Funktion häufig zu berechnen, so kann man etwa eine
Größenordnung an Rechenzeit einsparen. Der Vorteil der universellen Funktion
wird noch etwas größer, wenn man verlangt, dass das Ergebnis in einem Array
oder in einer Liste abgespeichert wird. In der Funktion sin_numpy ist das
bereits der Fall, nicht jedoch in der Funktion sin_math.
Wegen der genannten Rechenzeitvorteile lohnt es sich, einen Blick in die Liste der von NumPy zur Verfügung gestellten mathematischen Funktionen zu werfen.
Lineare Algebra¶
Physikalische Fragestellungen, die sich mit Hilfe von Vektoren und Matrizen formulieren lassen,
benötigen zur Lösung sehr häufig Methoden der linearen Algebra. NumPy leistet hierbei Unterstützung,
insbesondere mit dem linalg-Paket. Im Folgenden gehen wir auf einige Aspekte ein, ohne
Vollständigkeit anzustreben. Daher empfiehlt es sich, auch einen Blick in den
entsprechenden Abschnitt der Dokumentation
zu werfen. Zunächst importieren wir die Module, die wir für die Beispiele dieses Kapitels benötigen:
In [1]: import numpy as np
In [2]: import numpy.linalg as LA
Beim Arbeiten mit Matrizen und NumPy muss man immer bedenken, dass der Multiplikationsoperator * nicht für eine Matrixmultiplikation steht. Vielmehr wird damit eine elementweise Multiplikation ausgeführt:
In [3]: a1 = np.array([[1, -3], [-2, 5]])
In [4]: a1
Out[4]:
array([[ 1, -3],
[-2, 5]])
In [5]: a2 = np.array([[3, -6], [2, -1]])
In [6]: a2
Out[6]:
array([[ 3, -6],
[ 2, -1]])
In [7]: a1*a2
Out[7]:
array([[ 3, 18],
[-4, -5]])
Möchte man dagegen eine Matrixmultiplikation ausführen, so verwendet man das dot-Produkt:
In [8]: np.dot(a1, a2)
Out[8]:
array([[-3, -3],
[ 4, 7]])
Ab Python 3.5 und NumPy 1.10 steht hierfür auch ein spezieller Operator zur Verfügung.
In [9]: a1 @ a2
Out[9]:
array([[-3, -3],
[ 4, 7]])
Man könnte die Norm eines Vektors ebenfalls mit Hilfe des dot-Produkts bestimmen. Es bietet
sich jedoch an, hierzu direkt die norm-Funktion zu verwenden:
In [10]: vec = np.array([1, -2, 3])
In [11]: LA.norm(vec)
Out[11]: 3.7416573867739413
In [12]: LA.norm(vec)**2
Out[12]: 14.0
Als nächstes wollen wir ein inhomogenes lineares Gleichungssystem ax = b lösen, wobei die
Matrix a und der Vektor b gegeben sind und der Vektor x gesucht ist.
In [13]: a = np.array([[2, -1], [-3, 2]])
In [14]: b = np.array([1, 2])
In [15]: LA.det(a)
Out[15]: 0.99999999999999978
In [16]: np.dot(LA.inv(a), b)
Out[16]: array([ 4., 7.])
In Eingabe 15 haben wir zunächst überprüft, dass die Determinante der Matrix
a ungleich Null ist, so dass die invertierte Matrix existiert. Anschließend
haben wir den Vektor b von links mit der Inversen von a multipliziert,
um den Lösungsvektor zu erhalten. Allerdings erfolgt die numerische Lösung
eines inhomogenen linearen Gleichungssystems normalerweise nicht über eine
Inversion der Matrix, sondern mit Hilfe einer geeignet durchgeführten Gauß-Elimination.
NumPy stell hierzu die solve-Funktion zur Verfügung:
In [17]: LA.solve(a, b)
Out[17]: array([ 4., 7.])
Eine nicht invertierbare Matrix führt hier wie auch bei der Bestimmung der Determinante
auf eine LinAlgError-Ausnahme mit dem Hinweis auf eine singuläre Matrix.
Eine häufig vorkommende Problemstellung im Bereich der linearen Algebra sind
Eigenwertprobleme. Die eig-Funktion bestimmt rechtsseitige Eigenvektoren und
die zugehörigen Eigenwerte für beliebige quadratische Matrizen:
In [18]: a = np.array([[1, 3], [4, -1]])
In [19]: evals, evecs = LA.eig(a)
In [20]: evals
Out[20]: array([ 3.60555128, -3.60555128])
In [21]: evecs
Out[21]:
array([[ 0.75499722, -0.54580557],
[ 0.65572799, 0.83791185]])
In [22]: for n in range(evecs.shape[0]):
print(np.dot(a, evecs[:, n]), evals[n]*evecs[:, n])
Out[22]:
[ 2.72218119 2.36426089] [ 2.72218119 2.36426089]
[ 1.96792999 -3.02113415] [ 1.96792999 -3.02113415]
Die Ausgabe am Ende zeigt, dass die Eigenvektoren und -werte in der Tat korrekt
sind. Zudem wird hier deutlich, dass die Eigenvektoren als Spaltenvektoren in
der Matrix evecs gespeichert sind. Benötigt man nur die Eigenwerte einer
Matrix, so kann man durch Benutzung der eigvals-Funktion Rechenzeit sparen.
Für die Lösung eines Eigenwertproblems von symmetrischen oder hermiteschen [3]
Matrizen gibt es die Funktionen eigh und eigvalsh, bei denen es genügt,
nur die obere oder die untere Hälfte der Matrix zu spezifizieren. Viel
wichtiger ist jedoch, dass diese Funktionen einen erheblichen Zeitvorteil
bieten können:
In [23]: a = np.random.random(250000).reshape(500, 500)
In [24]: a = a+a.T
In [25]: %timeit LA.eig(a)
1 loop, best of 3: 209 ms per loop
In [26]: %timeit LA.eigh(a)
10 loops, best of 3: 28.2 ms per loop
Hier wird in Eingabe 24 durch Addition der Transponierten eine symmetrische
Matrix erzeugt, so dass die beiden Funktionen eig und eigh mit der
gleichen Matrix arbeiten. Die Funktion eigh ist in diesem Beispiel etwa
siebenmal so schnell.
Einfache Anwendungen¶
In diesem Abschnitt stellen wir einige einfache Problemstellungen vor, die sich mit Hilfe von NumPy gut bearbeiten lassen. Wir verzichten dabei bewusst auf die Angabe der Lösung, zeigen jedoch die zu erwartenden Resultate.
Mandelbrot-Menge¶
Betrachtet man die Rekursionsformel \(z_{n+1} = z_n^2+c\) mit \(z_0=0\), so ist die Mandelbrot-Menge durch die komplexen Zahlen \(c\) definiert, für die Folge der \(z_n\) beschränkt bleibt. Überschreitet der Betrag von \(z\) die Schwelle 2, so divergiert die Folge. In der Praxis wird man natürlich nur eine endliche Zahl von Iterationen ausführen können.
In der linken der beiden folgenden Abbildung ist die Mandelbrot-Menge in weiß dargestellt. Bei der Berechnung wird man möglicherweise Überlaufwarnungen erhalten. Diese kann man vermeiden, wenn man die Berechnung nur für die Werte von \(c\) fortsetzt, für die die Schwelle von Zwei noch nicht überschritten wurde. Dann eröffnet sich auch die Möglichkeit, die Zahl der Iterationen bis zum Erreichen der Schwelle abzuspeichern und in einer Farbabbildung darzustellen. Dies ist im rechten Bild für einen Ausschnitt gezeigt.
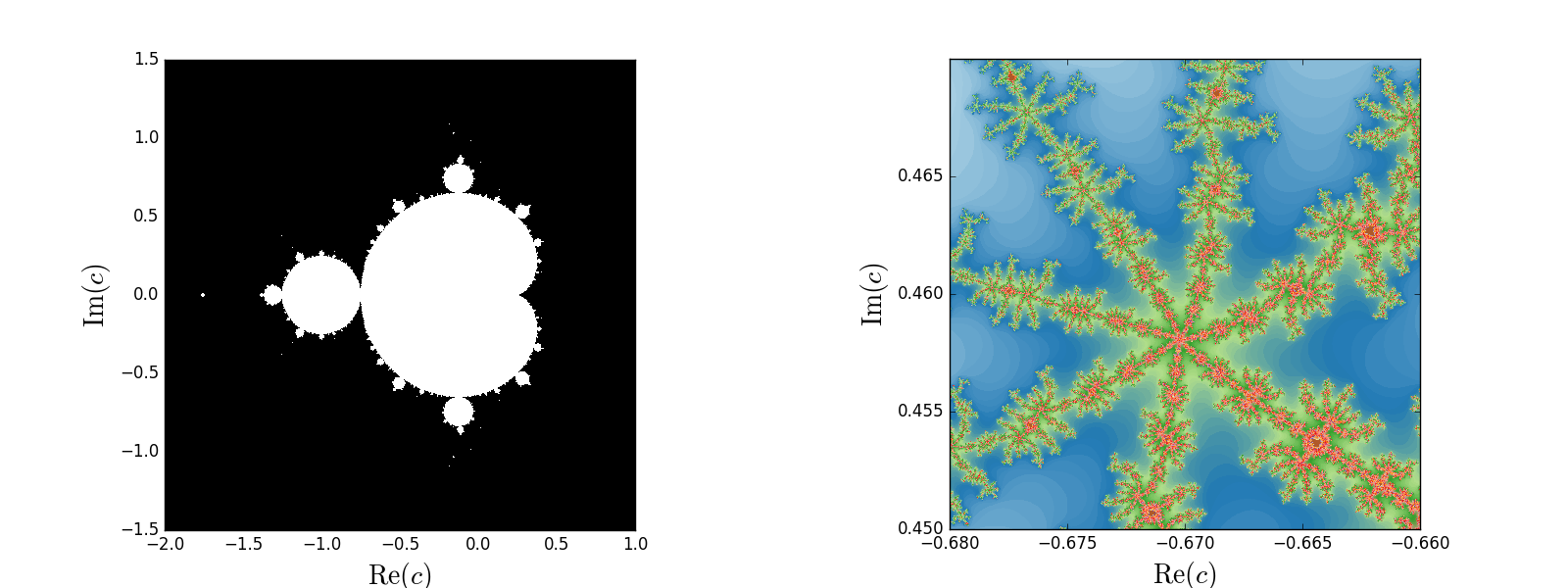
Brownsche Bewegung¶
Eine Zufallsbewegung in einer Dimension kann man durch Zufallszahlen darstellen, die aus der Menge der beiden Zahlen \(-1\) und \(1\) gezogen werden. Jede Zufallszahl gibt die Richtung an, in der zu dem entsprechenden Zeitpunkt ein Schritt ausgeführt wird. Es sollen nun mehrere Realisierung erzeugt und graphisch dargestellt werden. Aus den erzeugten Daten soll auch der Mittelwert und die Varianz des Orts als Funktion der Zeit berechnet und dargestellt werden. Für die Berechnung ist es praktisch, dass NumPy eine Funktion zur Verfügung stellt, die für ein Array sukzessive kumulative Summen berechnen kann.
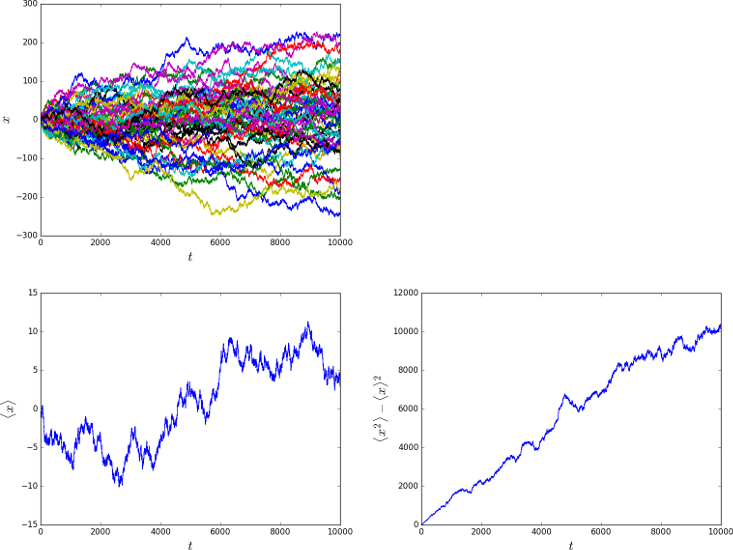
Fibonacci-Zahlen und goldener Schnitt¶
Die Fibonacci-Folge ist durch die Rekursionsformel \(f_{n+1} = f_n+f_{n-1}\)
mit den Anfangswerten \(f_1=f_2=1\) bestimmt. Das Verhältnis
\(f_{n+1}/f_{n}\) geht für große \(n\) gegen einen Grenzwert, der mit
Hilfe des linalg-Moduls von NumPy berechnet werden soll. Dies gelingt, wenn
man die Rekursionsformel als Abbildung des Tupels \((f_n, f_{n-1})\) auf
das Tupel \((f_{n+1}, f_n)\) interpretiert.
Bildbearbeitung¶
NumPy-Arrays können auch Bilddaten repräsentieren, so dass sich die Bearbeitung eines Bildes auf die Manipulation eines NumPy-Arrays zurückführen lässt. Der folgende Code zeigt, wie man ein in der SciPy-Bibliothek verfügbares Bild als Array interpretieren und graphisch darstellen kann.
In [1]: from scipy import misc
In [2]: face = misc.face(gray=True)
In [3]: face
Out[3]:
array([[114, 130, 145, ..., 119, 129, 137],
[ 83, 104, 123, ..., 118, 134, 146],
[ 68, 88, 109, ..., 119, 134, 145],
...,
[ 98, 103, 116, ..., 144, 143, 143],
[ 94, 104, 120, ..., 143, 142, 142],
[ 94, 106, 119, ..., 142, 141, 140]], dtype=uint8)
Wir haben es hier mit einem Array zu tun, dessen Elemente durch vorzeichenlose 8-Bit-Integers dargestellt sind, also Zahlen zwischen 0 und 255 repräsentieren. Diese können wir als Grauwerte darstellen.
In [4]: plt.imshow(face, cmap=plt.cm.gray)

Durch geeignete Manipulation des NumPy-Arrays face lässt sich das Bild in
ein Schwarz-Weiß-Bild verwandeln oder man kann die Kontrastkurve verändern.
Des Weiteren kann man das Bild zum Beispiel mit verschiedenen Rahmen versehen.
Einige Möglichkeiten zeigen die folgenden Bilder.
