Erstellung von Grafiken mit matplotlib¶

Bei matplotlib gibt es verschiedene Wege zur Erstellung einer Grafik. Man kann entweder das zu matplotlib gehörige pylab-Modul laden oder in IPython das magische Kommando %pylab verwenden. Dieser Weg führt dazu, dass umfangreiche Namensräume importiert werden, was einerseits der Bequemlichkeit dient, andererseits aber den Nachteil besitzt, dass häufig schwer nachzuvollziehen ist, woher eine bestimmte Funktion stammt. Daher ist von der Benutzung des pylab-Moduls eher abzuraten, und wir werden es im Folgenden auch nicht verwenden.

Eine zweite Variante besteht in der Benutzung des pyplot-Moduls aus matplotlib. Dieses Modul erlaubt es, den Zustand einer Grafik zu verändern und eignet sich daher besonders für die interaktive Entwicklung von Grafiken, zum Beispiel in einer IPython-Shell oder einem IPython-Notebook. Die Verwendung von pyplot ist aber genauso in einem normalen Python-Skript möglich. Die meisten der im Folgenden besprochenen Beispiele verwenden pyplot.

Schließlich bietet matplotlib einen objektorientierten Zugang, den wir in den letzten Beispiele dieses Kapitels etwas kennenlernen werden.

Um mit matplotlib arbeiten zu können, müssen zunächst die benötigten Module importiert werden:

In [1]: import numpy as np
   ...: import matplotlib as mpl
   ...: import matplotlib.pyplot as plt
   ...: %matplotlib
Using matplotlib backend: Qt5Agg

In den meisten Fällen wird hierzu das NumPy-Modul gehören, das wir wie gewohnt unter der Abkürzung np in der ersten Zeile importieren. Für die Arbeit mit pyplot wird der Importbefehl in der dritten Zeile benötigt, wobei wir uns hier an die Konvention halten, für pyplot die Abkürzung plt zu verwenden. Da wir gelegentlich das matplotlib-Modul selbst benötigen, um die Fähigkeiten von matplotlib zu demonstrieren, importieren wir es in der zweiten Zeile. Hierauf kann man in vielen Fällen verzichten.

Für die interaktive Arbeit in der IPython-Shell wird abschließend noch das magische Kommando %matplotlib verwendet. Arbeitet man mit einem Python-Skript, so entfällt dieser Schritt. Wenn man mit einem IPython-Notebook arbeitet, so hat man noch die Möglichkeit, Grafiken direkt in das Notebook einzubetten. In diesem Fall lautet das magische Kommando %matplotlib inline.

Wir wollen nun eine einfache Grafik erstellen, deren Eigenschaften wir im Weiteren schrittweise verändern werden. Zunächst erzeugen wir drei NumPy-Arrays, die die Daten für zwei Funktionen enthalten, die wir grafisch darstellen wollen.

In [2]: x = np.linspace(0, 10, 30)
   ...: y1 = np.cos(x)
   ...: y2 = np.sin(x)

Nun können wir leicht eine Grafik erzeugen, die die beiden Funktionen darstellt.

In [3]: plt.plot(x, y1)
   ...: plt.plot(x, y2)
Out[3]: [<matplotlib.lines.Line2D at 0x7f48b0a01320>]

Führt man diese beiden Kommandos aus, so öffnet sich ein Fenster, das neben der Grafik auch einige Icons enthält, die es erlauben, die Darstellung zu modifizieren. [4]

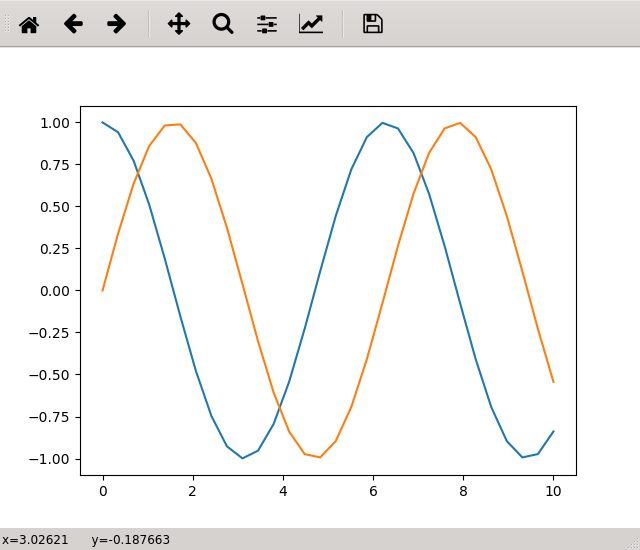
Die acht Icons haben von links nach rechts die folgenden Funktionen:

• Nachdem man mit Hilfe der anderen Icons Veränderungen an der Grafik vorgenommen hat, kann man mit diesem Icon wieder zur ursprünglichen Darstellung zurückkehren.
• Mit diesem Icon kommt man zur vorhergehenden Darstellung zurück.
• Ist man zu einer früheren Darstellung zurückgegangen, so kommt man mit diesem Icon zu neueren Darstellungen.
• Mit diesem Icon lässt sich der Bildausschnitt verschieben.
• Mit diesem Icon lässt sich ein kleinerer Bildausschnitt durch Aufziehen eines Rechtecks wählen. Man kann also bei Bedarf in die Abbildung hineinzoomen.
• Dieses Icon erlaubt es, die Seitenverhältnisse der Abbildung und die Größe der Ränder zu verändern.
• Dieses Icon ist nicht bei jedem Backend vorhanden, wird aber bei dem hier verwendeten Qt-Backend angezeigt. Es erlaubt die Wahl des x- und y-Achsenabschnitts, das Setzen von Beschriftungen sowie die Wahl von logarithmischen Achsen. Je nach Art der Grafik lässt sich hier zum Beispiel auch die Farbpalette einstellen. Diese Funktionalität ist aber auch durch entsprechende pyplot-Funktionen verfügbar, wie wir im Folgenden sehen werden.
• Das letzte Icon dient dazu, die Grafik in einer Datei zu speichern, sei es in einem Bitmap-Format wie zum Beispiel png oder in einem Vektorgrafik-Format wie eps, pdf oder svg.

Bevor wir uns aber mit der Beschriftung der Grafik beschäftigen, wollen wir uns zunächst der Darstellung der Daten zuwenden. Standardmäßig werden die Daten mit Hilfe einer durchgezogenen Kurve dargestellt, deren Farbe von einem Datensatz zum nächsten automatisch wechselt. Wir wollen nun die Darstellung dieser Kurven verändern. Dazu beschaffen wir uns zunächst die beiden Linien

In [4]: line1, line2 = plt.gca().lines

gca steht hier für »get current axes«, das die aktuelle Untergrafik zurückgibt. In unserem Fall handelt es sich einfach um die aktuelle Grafik. Da aber eine Abbildung, wie wir später noch sehen werden, aus mehreren Untergrafiken bestehen kann, ist es im Prinzip wichtig, zwischen einer Untergrafik und der gesamten Abbildung zu unterscheiden. Mit Hilfe des lines-Attributes kann man eine Liste der aktuell vorhandenen Linien erhalten. Da wir wissen, dass es sich um zwei Linien handelt, können wir die Liste direkt entpacken.

Nachdem wir nun Zugriff auf die Linien haben, können wir deren Eigenschaften ändern. Dazu gibt es zwei Möglichkeiten, wie wir hier am Beispiel der Linienbreite zeigen wollen. Man kann die Linienbreite durch eine entsprechende Methode setzen, wobei man anschließend die Grafik mit einer draw-Anweisung in dem noch geöffneten Fenster neu erzeugen muss.

In [5]: line1.set_linewidth(5)
   ...: plt.draw()

Das Ergebnis sieht dann folgendermaßen aus:

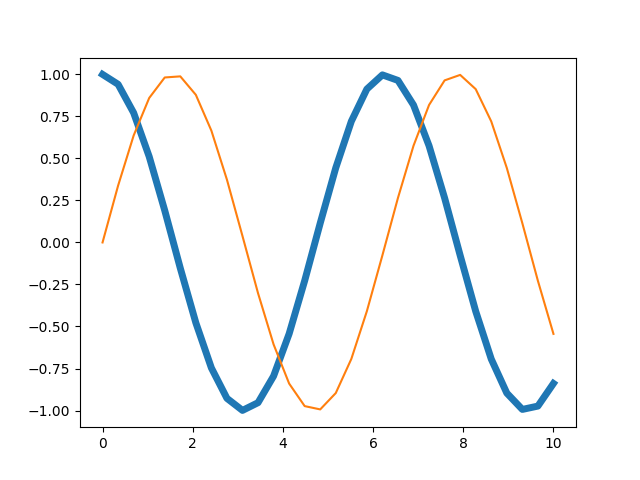
Alternativ kann man die setp-Methode verwenden, die es erlaubt, Eigenschaften zu setzen (»set properties«), in diesem Fall die Linienbreite der zweiten Linie.

In [6]: plt.setp(line2, linewidth=10)

Die Grafik hat danach das folgende Aussehen:

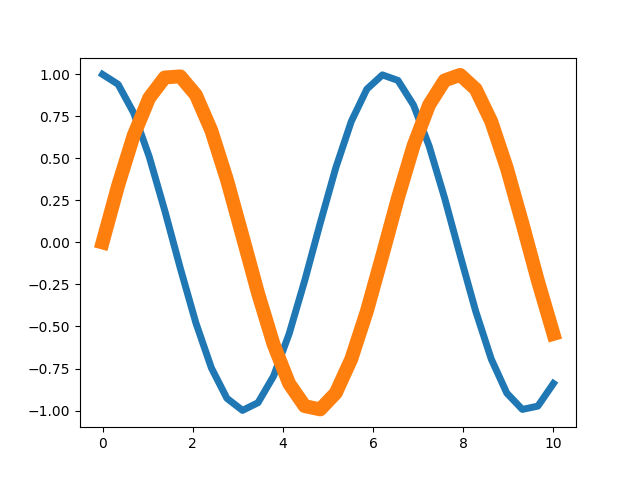
Im nächsten Schritt wollen wir die Farben der beiden Linien verändern und verwenden dafür wieder die setp-Methode,

In [7]: plt.setp(line1, color='m')

und erhalten folgende Ausgabe:

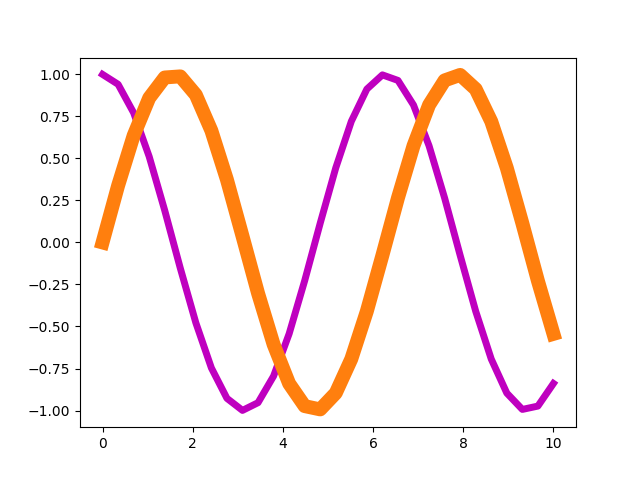
In diesem Beispiel haben wir ausgenutzt, dass sich eine Reihe von Farben mit Hilfe eines Buchstabens auswählen lassen, nämlich

In [8]: mpl.colors.BASE_COLORS
Out[8]: {'b': (0, 0, 1),
         'c': (0, 0.75, 0.75),
         'g': (0, 0.5, 0),
         'k': (0, 0, 0),
         'm': (0.75, 0, 0.75),
         'r': (1, 0, 0),
         'w': (1, 1, 1),
         'y': (0.75, 0.75, 0)}

Es stehen auf diese Weise also die Farben Blau (b), Cyan (c), Grün (g), Schwarz (k), Magenta (m), Rot (r), Weiß (w) und Gelb (y) zur Verfügung. Die aufgelisteten Tupel geben die RGB-Darstellung der jeweiligen Farben an, das heißt den Anteil der Farben Rot, Grün und Blau. Dieses ist direkt an den Farben Rot und Blau nachvollziehbar. Bei Grün ist die Helligkeit reduziert, da diese Farbe bei voller Helligkeit im Allgemeinen schlecht zu sehen ist. Bei Weiß haben alle drei Kanäle ihren Maximalwert, während bei Schwarz keiner der Kanäle beiträgt. Bei den Komplementärfarben Cyan, Magenta und Gelb sind zwei der drei Kanäle beteiligt.

Eine große Zahl von Farben lässt sich durch Angabe eines Farbnamens erhalten, wobei man sich eine vollständige Liste der verfügbaren Namen anzeigen lassen kann.

In [9]: mpl.colors.cnames
Out[9]: {'aliceblue': '#F0F8FF', 'antiquewhite': '#FAEBD7', 'aqua': '#00FFFF',
         'aquamarine': '#7FFFD4', 'azure': '#F0FFFF', 'beige': '#F5F5DC',
         ...
         'violet': '#EE82EE', 'wheat': '#F5DEB3', 'white': '#FFFFFF',
         'whitesmoke': '#F5F5F5', 'yellow': '#FFFF00', 'yellowgreen': '#9ACD32'}

Jeder Farbe ist wieder ein RGB-Wert zugeordnet, der in diesem Fall hexadezimal kodiert ist. Der RGB-Wert besteht hier aus drei zweistelligen Hexadezimalzahlen, die demnach Werte zwischen 0 und 255 repräsentieren. Um auf die obige RGB-Darstellung zu kommen, muss man das Intervall von 0 bis 255 auf das Intervall von 0 bis 1 abbilden, also durch 255 teilen.

Die obige Liste der verfügbaren Farbnamen ist nicht vollständig wiedergegeben. Für die Farbauswahl praktischer ist die folgende, daraus erstellte Farbtabelle, die mit Hilfe des Skripts named_colors.py aus der matplotlib-Galerie erzeugt werden kann.

Als Beispiel ändern wir die Farbe der zweiten Linie auf seagreen

In [10]: plt.setp(line2, color='seagreen')

und erhalten damit die folgende Ausgabe

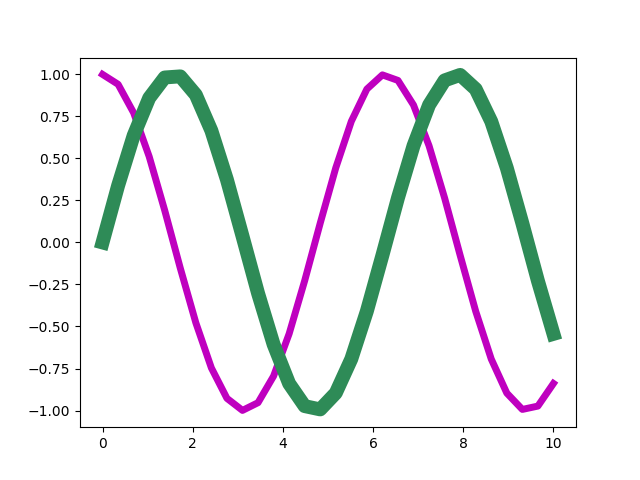
Falls die bisher genannten Farben nicht ausreichen sollten, kann man Farben auch stufenlos wählen, wenn man von der endlichen Auflösung der Gleitkommazahlen in Python absieht. So lassen sich Grautöne kontinuierlich von Schwarz bis Weiß mit Hilfe einer Zahl zwischen 0 und 1 festlegen. In dem folgenden Beispiel wird für die erste Linie ein Grauton vorgegeben.

In [11]: plt.setp(line1, color='0.5')

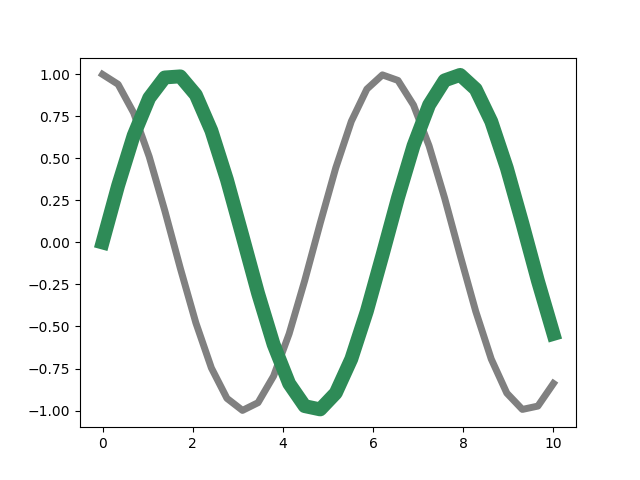
Wie bereits weiter oben beschrieben, lassen sich Farben in der RGB-Darstellung hexadezimal oder durch ein aus drei Zahlen bestehendes Tupel auswählen, wie die folgenden beiden Beispiele zeigen.

In [12]: plt.setp(line1, color='#FFC000')

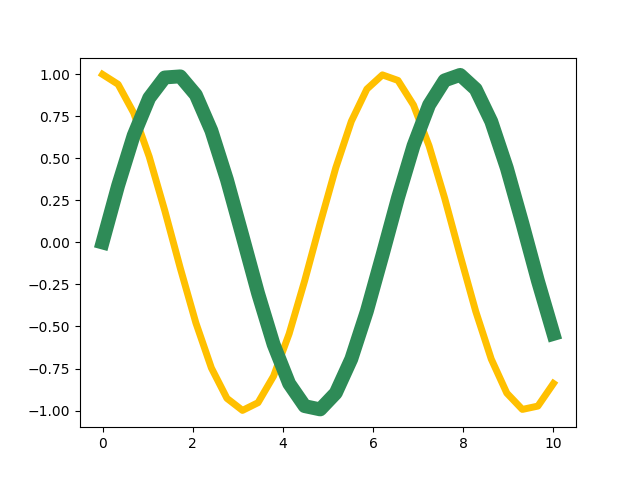
In [13]: plt.setp(line1, color=(0, 0.7, 1))

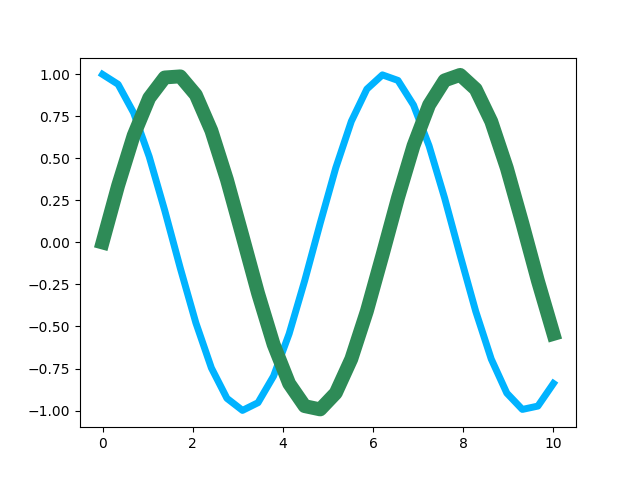
Alternativ zum RGB-System lassen sich Farben auch mit Hilfe des HSV-Systems darstellen, in dem die Farben ebenfalls durch ein Tupel aus drei Gleitkommazahlen zwischen 0 und 1 charakterisiert werden. Der erste Wert steht für den Farbton (»hue«) und gibt die Position im Farbkreis an. Dabei sind die Werte 0 und 1 der Farbe Rot zugeordnet. Grün liegt bei 1/3 und Blau bei 2/3. Der zweite Wert gibt die Farbsättigung (»saturation«) an. Verringert man diesen Wert, so geht man von der Farbe zu einem entsprechenden Grauton über. Der dritte Wert (»value«) schließlich beeinflusst die Helligkeit der Farbe.

Im folgenden Beispiel setzen wir den ersten Wert auf 0.3 und wählen so einen Grünton aus. Wie schon weiter oben erwähnt, besteht bei Grüntönen die Gefahr, dass sie zu hell erscheinen. Daher haben wir für die zweite Linie den dritten Wert des Tupels reduziert.

In [14]: plt.setp(line1, color=mpl.colors.hsv_to_rgb((0.3, 1, 1)))
   ...: plt.setp(line2, color=mpl.colors.hsv_to_rgb((0.3, 1, 0.6)))

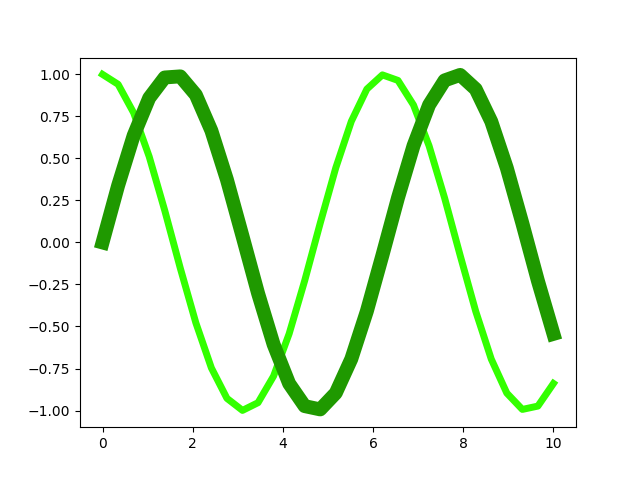
Um Unterschiede zwischen verschiedenen Linien hervorzuheben, kann man nicht nur verschiedene Farben einsetzen, sondern auch unterschiedliche Linienarten. Dies ist besonders dann sinnvoll, wenn man davon ausgehen muss, dass die Abbildung in schwarz/weiß gedruckt wird, so dass Farben auf Grautöne abgebildet würden.

Die Linienart wird in matplotlib durch einen String charakterisiert, der sich aus der folgenden Auflistung ergibt.

In [15]: mpl.lines.Line2D.lineStyles
Out[15]: {'': '_draw_nothing',
          ' ': '_draw_nothing',
          '-': '_draw_solid',
          '--': '_draw_dashed',
          '-.': '_draw_dash_dot',
          ':': '_draw_dotted',
          'None': '_draw_nothing'}

Möchte man eine Linie gestrichelt darstellen, kann man wie bei den Farben die setp-Methode verwenden und übergibt mit Hilfe des Schlüsselworts linestyle den entsprechenden Wert '--'.

In [16]: plt.setp(line2, linestyle='--')

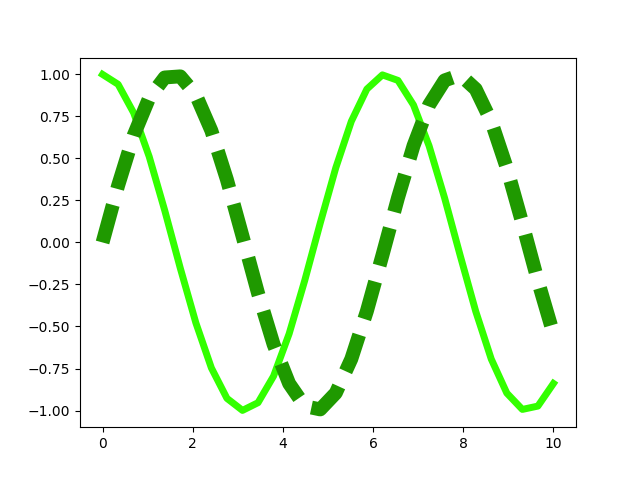
Bei Bedarf kann man die Strichlänge anpassen oder auch die Form der Strichenden festlegen.

In [17]: plt.setp(line2, dashes=(6, 2))

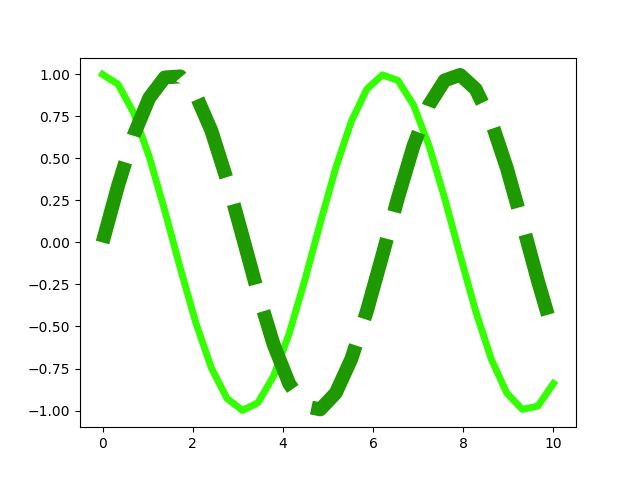
In [18]: plt.setp(line2, dashes=(4, 2), dash_capstyle='round')

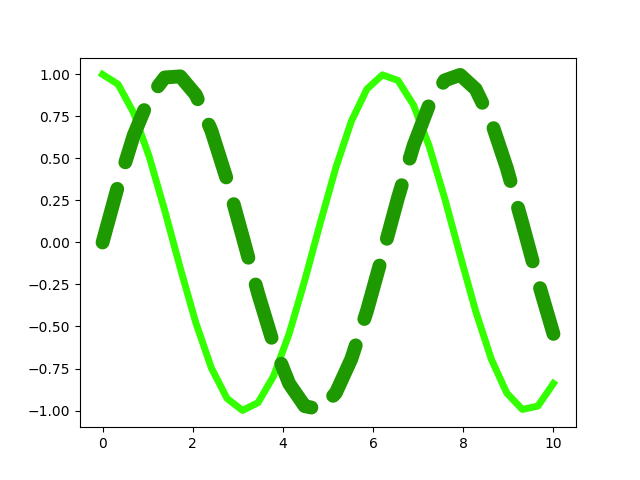
Vor allem bei Linienverläufen, die Spitzen enthalten, kann es interessant sein, die Form vorzugeben, mit der Linien aneinander gefügt werden. Es gibt hierfür drei Möglichkeiten, die im Folgenden dargestellt sind.

In [19]: plt.cla()
   ...: xdata = np.array([0, 0.1, 0.5, 0.9, 1])
   ...: ydata = np.array([0, 0, 1, 0, 0])
   ...: for n in range(3):
   ...:     plt.plot(xdata, ydata+0.2*n)
   ...: line = plt.gca().lines
   ...: plt.setp(line, linewidth=20)
   ...: plt.ylim(0, 1.5)
   ...: for n, joinstyle in enumerate(('round', 'bevel', 'miter')):
   ...:     plt.setp(line[n], solid_joinstyle=joinstyle)

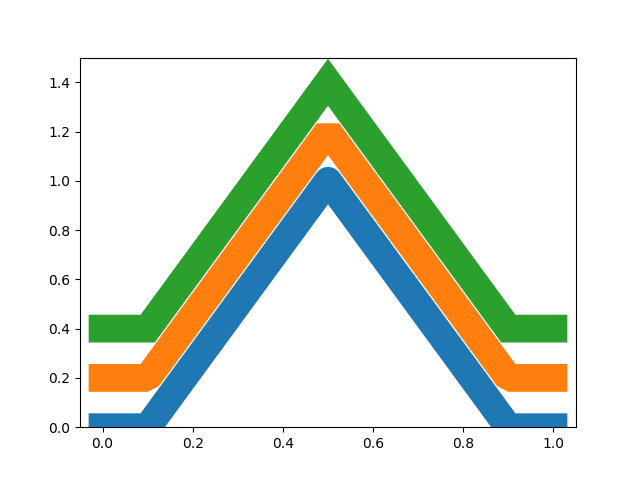
In dem obigen Codebeispiel haben wir eine Funktion verwendet, die bis jetzt noch nicht besprochen wurde, nämlich cla(). Der Name steht für »clear current axes« und löscht die aktuellen Unterabbildung, die in unserem Fall einfach der aktuellen Abbildung entspricht.

Bis jetzt haben wir die Datenpunkte lediglich durch Linien dargestellt. Dies ist jedoch häufig entweder nicht gewünscht oder nicht ausreichend. Insbesondere bei Messdaten sollen die Datenpunkte oft einzeln markiert werden. In vielen Fällen kann man bei matplotlib auf eine sehr einfache Syntax zurückgreifen. Um dies zu illustrieren, erstellen wir unsere Beispielgrafik, mit der wir bisher überwiegend gearbeitet haben, neu. Im ersten plot-Aufruf verwenden wir als drittes Argument die Zeichenkette 'ro-'. Das erste Zeichen, r, wird als Farbe interpretiert und bedeutet, wie wir bereits wissen, Rot. Das zweiten Zeichen, o, wird als Symbol interpretiert, in diesem Fall als Kreis. Der abschließende Bindestrich gibt an, dass nicht nur Symbole dargestellt werden sollen, sondern die Symbole außerdem durch eine durchgezogene Linie verbunden werden sollen. Für den zweiten Datensatz verlangen wir mit 'yD-' statt roten Kreisen gelbe Rauten (»diamonds«).

In [20]: plt.cla()
   ...: plt.plot(x, y1, 'ro-')
   ...: plt.plot(x, y2, 'yD-')
Out[20]: [<matplotlib.lines.Line2D at 0x7f48b0110860>]

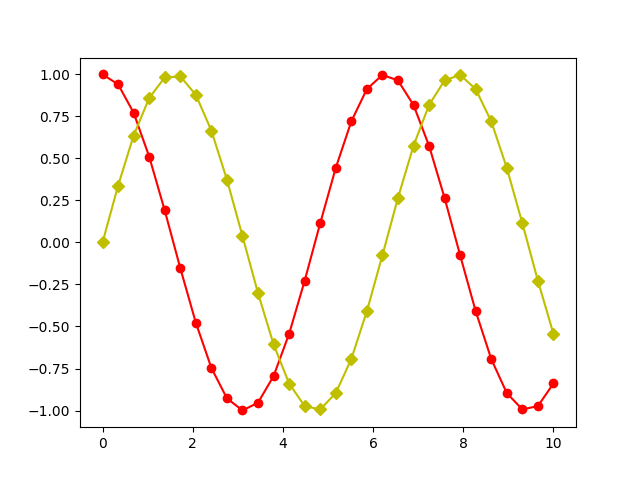
Um die Symbole modifizieren zu können, verschaffen wir uns Zugriff auf die einzelnen Linie, wie wir dies früher schon getan haben.

In [21]: line1, line2 = plt.gca().lines

Zunächst verändern wir die Größe der Symbole. Dazu beschaffen wir uns zunächst den aktuellen Wert, um eines der Symbole relativ zu diesem Wert vergrößern und das andere verkleinern zu können. Hierzu verwenden wir die Partnermethode zu setp. nämlich getp, das für »get property« steht, es also erlaubt, Eigenschaften in Erfahrung zu bringen.

In [22]: plt.getp(line1, 'markersize')
Out[22]: 6.0

Die Standardgröße der Symbole beträgt also 6, so dass wir davon ausgehend nun mit der bewährten setp-Methode neue Sybolgrößen setzen können.

In [23]: plt.setp(line1, markersize=4)
   ...: plt.setp(line2, markersize=10)

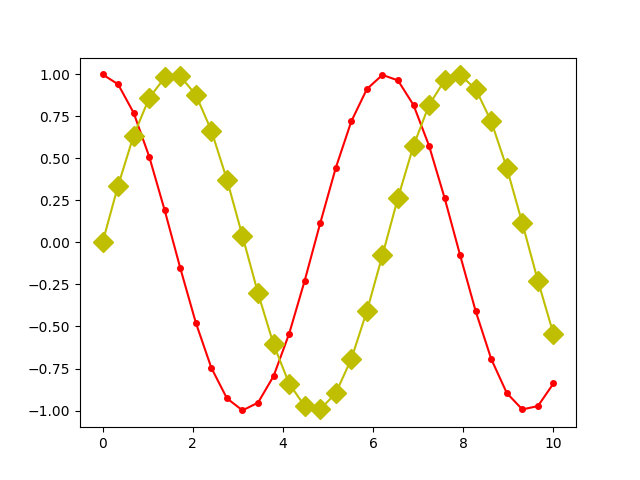
Neben Kreisen und Rauten stellt matplotlib natürlich noch weitere Symbole zur Verfügung, die man sich als Dictionary ausgeben lassen kann.

In [24]: mpl.lines.Line2D.markers
Out[24]: {'.': 'point', ',': 'pixel', 'o': 'circle', 'v': 'triangle_down',
          ...
          8: 'caretleftbase', 9: 'caretrightbase', 10: 'caretupbase',
          11: 'caretdownbase', 'None': 'nothing', None: 'nothing',
          ' ': 'nothing', '': 'nothing'}

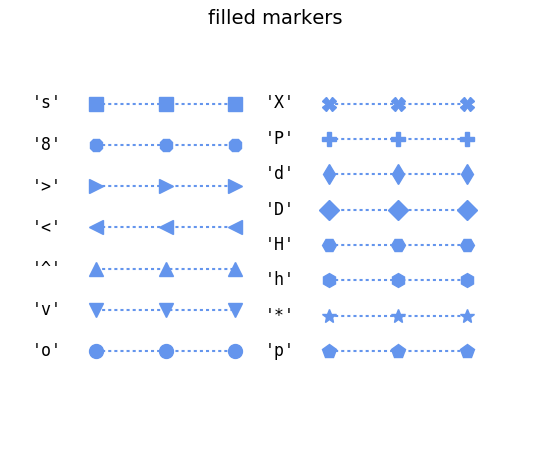
Das Dictionary ist hier nur auszugsweise wiedergegeben, da die folgende grafische Darstellung nützlicher ist. Zu beachten ist, dass zwar die meisten Symbole mit einem Zeichen ausgewählt werden, es aber dennoch einige Symbole gibt, auf die mit einer Ziffer Bezug genommen wird. So bezeichnen 4 und '4' unterschiedliche Symbole.

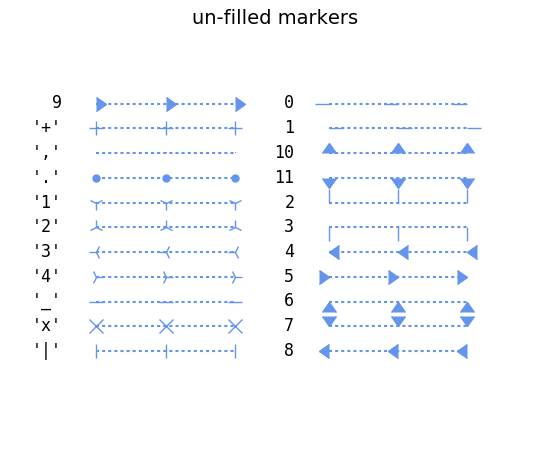
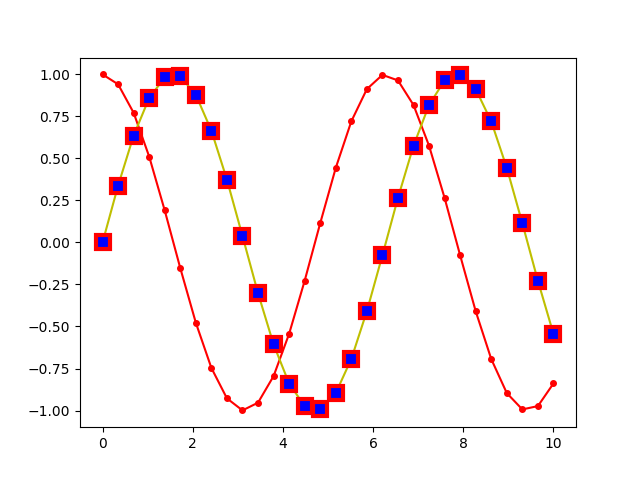
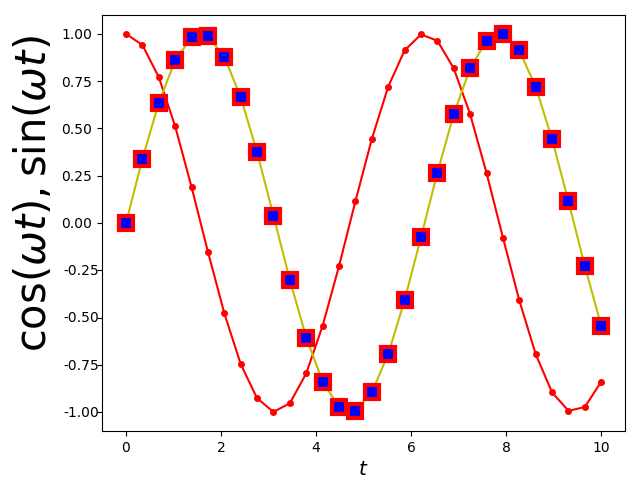
Bei Bedarf lassen sich die Eigenschaften von Symbolen im Detail festlegen. Das folgende Beispiel erzeugt auf der Linie 2 quadratische blaue Symbole mit einem roten Rand von 3 Punkten Breite.

In [25]: plt.setp(line2, marker='s', markerfacecolor='b',
   ...:          markeredgewidth=3, markeredgecolor='r')

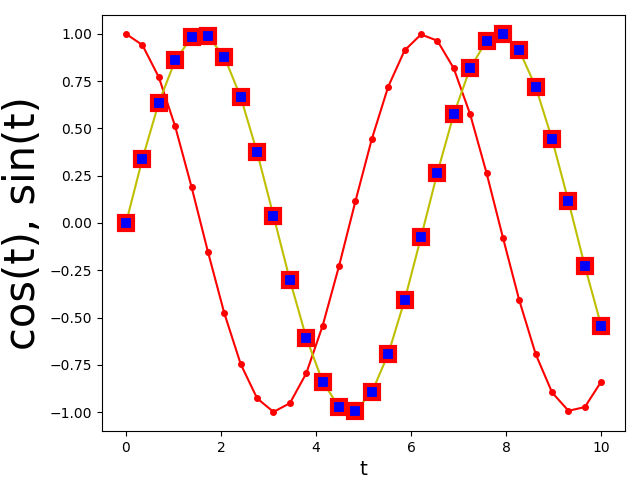
Zu einem ordentlichen Funktionsgraphen gehört selbstverständlich auch eine Achsenbeschriftung. Im einfachsten Fall verwendet man xlabel und ylabel und gibt den Text als Argument in Form einer Zeichenkette an. Häufig muss man allerdings die Schriftgröße anpassen. Dies kann mit Hilfe eines entsprechenden Bezeichners geschehen, wie es hier für die x-Achse erfolgt, oder aber durch Angabe einer Schriftgröße in Punkten, wie es hier für die y-Achse gezeigt ist.

In [26]: plt.xlabel('t', fontsize='x-large')
Out[26]: <matplotlib.text.Text at 0x7f48b0a30668>

In [27]: plt.ylabel('cos(t), sin(t)', fontsize=30)
Out[27]: <matplotlib.text.Text at 0x7f48b015a780>

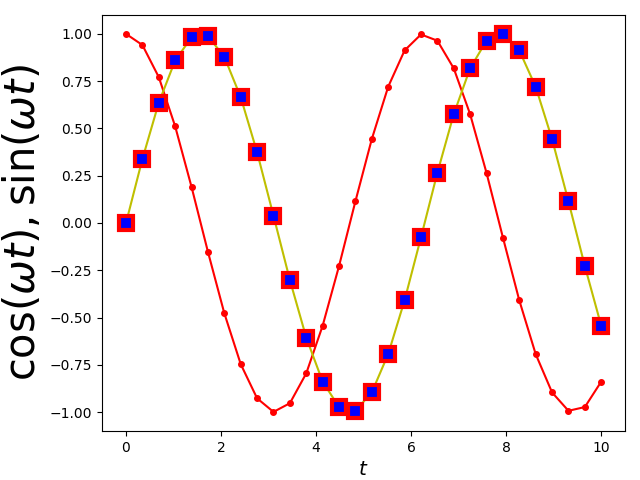
Einen besseren Mathematiksatz erhält man, wenn man die TeX-Syntax verwendet [5]. Dabei werden mathematische Teile in Dollarzeichen eingeschlossen, was unter anderem zur Konsequenz hat, dass mathematische Symbole kursiv dargestellt werden. TeX- und LaTeX-Kommandos beginnen mit \ und so lassen sich beispielsweise griechische Buchstaben durch Voranstellen dieses Zeichens vor den Namen des Buchstabens erzeugen. \omega wird so zu einem ω.

In [28]: plt.xlabel('$t$')
   ...: plt.ylabel(r'$\cos(\omega t), \sin(\omega t)$')
Out[28]: <matplotlib.text.Text at 0x7f48b015a780>

Standardmäßig interpretiert matplotlib selbst die in TeX-Syntax übergebenen Zeichenketten. Dabei wird nur ein Teil der äußerst umfangreichen Möglichkeiten von TeX unterstützt. Man kann jedoch auch verlangen, dass der Text von der lokal vorhandenen TeX-Installation gesetzt wird.

In [29]: mpl.rc('text', usetex = True)
   ...: plt.ylabel(r'$\cos(\omega t), \sin(\omega t)$')
Out[29]: <matplotlib.text.Text at 0x7f48b015a780>

Gelegentlich ist es sinnvoll, eine Grafik mit einer Legende zu versehen, die die Bedeutung der einzelnen Kurven erläutert. Eine Möglichkeit, den Beschriftungstext vorzugeben, besteht darin, dies gleich bei der Erzeugung der Kurven mit Hilfe der Variable label zu tun.

In [30]: plt.cla()
   ...: plt.plot(x, y1, 'o-', label='Kosinus')
   ...: plt.plot(x, y2, 's-', label='Sinus')
Out[30]: [<matplotlib.lines.Line2D at 0x7f48b09f9828>]

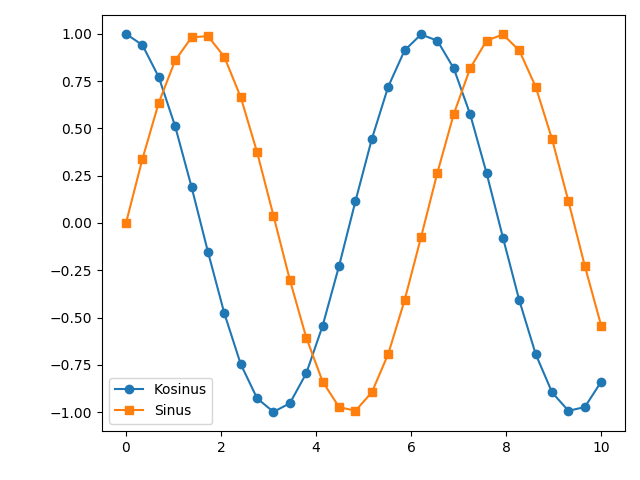
Die legend-Methode wird anschließend benutzt, um die Legende im Graphen zu setzen.

In [31]: plt.legend()
Out[31]: <matplotlib.legend.Legend at 0x7f48af928080>

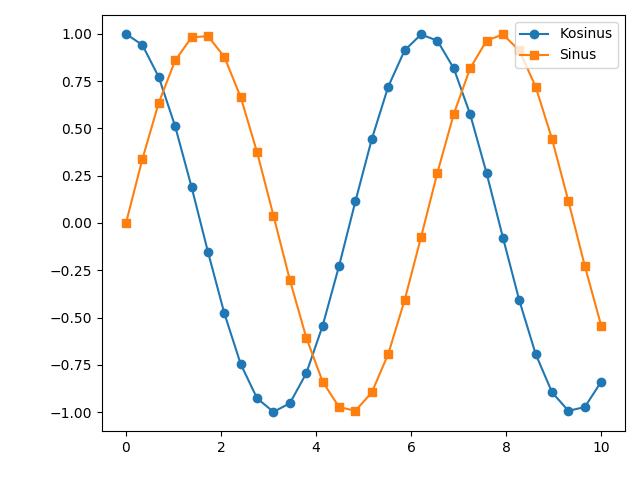
Man kann aber beispielsweise auch verlangen, dass die Legende rechts oben platziert wird.

In [32]: plt.legend(loc='upper right')
Out[32]: <matplotlib.legend.Legend at 0x7f48af946ba8>

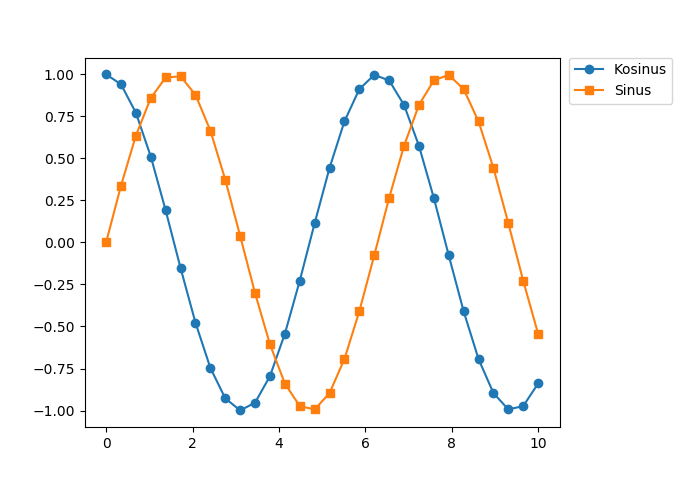
Steht ausreichend horizontaler Platz zur Verfügung, so kann es im vorliegenden Fall günstig sein, die Legende außerhalb der Grafik anzuordnen, wie das folgende Beispiel zeigt.

In [33]: plt.legend(bbox_to_anchor=(1.02, 1), loc='upper left', borderaxespad=0)
Out[33]: <matplotlib.legend.Legend at 0x7f48af8d4780>

Hier wird festgelegt, dass die Legende mit der oberen linken Ecke etwas außerhalb des rechten oberen Randes der Grafik platziert wird. Der genaue Punkt wird relativ zur so genannten »bounding box« angegeben, die hier immer die horizontale und vertikale Länge 1 besitzt, also unabhängig von den Problemkoordinaten ist, die hier in horizontaler Richtung von 0 bis 10 und in vertikaler Richtung von -1 bis 1 laufen. Der Punkt (1.02, 1) liegt somit wie behauptet leicht rechts von der oberen rechten Ecke der Grafik.

Die Achsen haben neben der bereits besprochenen Achsenbeschriftung noch weitere Eigenschaften, die sich in matplotlib einstellen lassen. So kann es sinnvoll sein, den Umfang der Achsen in Problemkoordinaten unabhängig von dem Bereich festzulegen, in dem sich die Daten befinden. Im folgenden Beispiel wird die x-Achse auf einen kleinen Ausschnitt der bisherigen Achse eingeschränkt.

In [34]: plt.xlim(4, 6)
Out[34]: (4, 6)

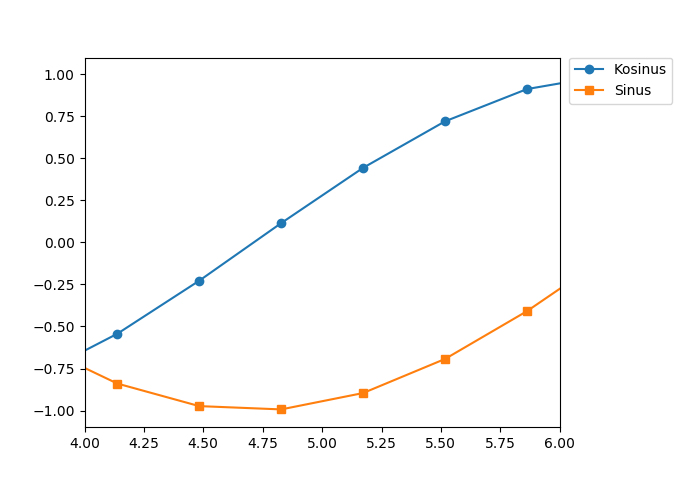
In [35]: plt.xlim(0, 10)
Out[35]: (0, 10)

Nachdem wir wieder zum ursprünglichen Achsenumfang zurückgekehrt sind, wollen wir die y-Achse logarithmisch darstellen. Dies hat in unserem Fall den Nebeneffekt, dass die Bereiche, in denen negative y-Werte auftreten, nicht dargestellt werden. Außerdem wollen wir ein Koordinatengitter für beide Achsen anzeigen lassen.

In [36]: plt.yscale('log')
   ...: plt.grid(which='both')

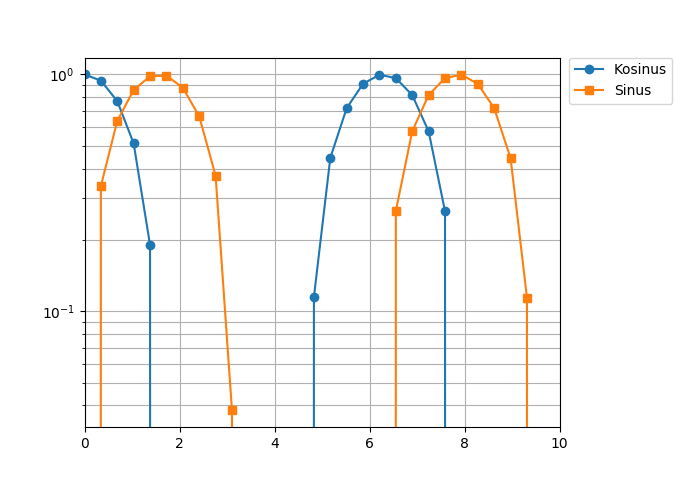
Der Wechsel zwischen linearer und logarithmischer Achse kann auch direkt im Grafikfenster mit Hilfe der Tasten k für die x-Achse und l für die y-Achse erfolgen. Dies ist besonders dann praktisch, wenn man nur schnell überprüfen möchte, wie Daten in einer einfach- oder doppelt-logarithmischen Auftragung aussehen.

In [37]: plt.yscale('linear')

Wieder zu einer linearen Skala zurückgekehrt, wollen wir noch an einem einfachen Beispiel zeigen, wie man die Achseneinteilung den jeweiligen Bedürfnissen anpassen kann. Eine genauere Diskussion der verschiedenen Möglichkeiten, die matplotlib zu diesem Zweck zur Verfügung stellt, würde hier zu weit führen.

Nachdem wir in unserer Beispielgrafik trigonometrische Funktionen darstellen, wollen wir gerne die x-Achse in Vielfache von π einteilen. Dies kann dadurch geschehen, dass wir der xticks-Methode eine Liste von Punkten auf der x-Achse sowie ein Tupel mit den entsprechenden Beschriftungen übergeben. Außerdem können wir Schrifteigenschaften festlegen, zum Beispiel die Schriftgröße und die Schriftfarbe, die wir hier rot wählen.

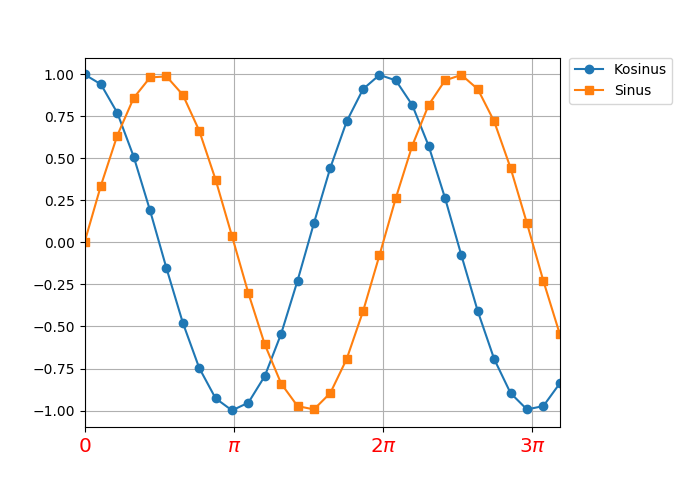
In [38]: plt.xticks(np.pi*np.arange(0, 4), ('0', r'$\pi$', r'$2\pi$', r'$3\pi$'),
   ...:            size='x-large', color='r')
Out[38]: ([<matplotlib.axis.XTick at 0x7f48b0a011d0>,
  <matplotlib.axis.XTick at 0x7f48b0178908>,
  <matplotlib.axis.XTick at 0x7f48b016ada0>,
  <matplotlib.axis.XTick at 0x7f48af92f8d0>],
 <a list of 4 Text xticklabel objects>)

Das Ergebnis sieht dann folgendermaßen aus:

Hat man die optimale Form für die Grafik erreicht, so möchte man diese häufig auch abspeichern. Wie wir schon gesehen haben, lässt sich das mit dem entsprechenden Icon im Grafikfenster erreichen. Genauso gut kann man die Grafik aber auch mit Hilfe der savefig-Funktion in einer Datei speichern. Dabei ist zunächst das gewünschte Format festzulegen.

Für die Darstellung auf einem Bildschirm oder zum Beispiel für die Einbindung in eine Webseite eignet sich ein Bitmapformat, das die Abbildung in einer gerasterten Form abspeichert. Hierfür gibt es sehr viele verschiedene Formate. In matplotlib bietet sich die Verwendung des png-Formats [6] an.

In [39]: plt.savefig('example.png')

Der Nachteil von Bitmapformaten ist, dass die Pixelstruktur der Abbildung bei einer vergrößerten Darstellung mehr oder weniger stark sichtbar wird. Benötigt man eine höher aufgelöste Ausgabe, beispielsweise zum Druck, so wird man eher zu einem Vektorformat greifen. matplotlib bietet hier das Postscript-Format an, das sich im Encapsulated Postscript-Format für die Einbettung in andere Dokumente eignet. Ein heute weit verbreitetes Format ist PDF (»portable document format«). Dieses Format kann auch Bitmap-Anteile enthalten, die dann natürlich der beschriebenen Skalierungsproblematik unterliegen. SVG (»scalable vector graphics«) ist ein Vektorgrafikformat, das für die Verwendung von Vektorgrafiken im Internet entwickelt wurde und von modernen Webbrowsern zumindest zu großen Teilen dargestellt werden kann.

In [40]: plt.savefig('example.pdf')

Die savefig-Funktion benötigt als zwingendes Argument den Namen der Datei, in der die Abbildung gespeichert werden soll. Sie akzeptiert außerdem eine Reihe weiterer Argumente, mit denen man zum Beispiel die Auflösung einer Bitmapgrafik oder die Hintergrundfarbe der Abbildung beeinflussen kann. Bei Bedarf empfiehlt sich ein Blick in die matplotlib-Dokumentation.

Abschließend wollen wir aus dem breiten Spektrum der Möglichkeiten von matplotlib noch drei Problemstellungen ansprechen, die in einem wissenschaftlichen Umfeld häufig vorkommen. Als erstes wollen wir uns mit der Darstellung von zweidimensionalen Daten mit Hilfe eines Konturplots beschäftigen.

Zunächst löschen wir die noch vorhandene Abbildung mit Hilfe der clf-Funktion (»clear figure«) und fangen auf diese Weise neu an.

In [41]: plt.clf()

Um Daten zur Verfügung zu haben, die wir darstellen können, verwenden wir NumPy, mit dem wir zunächst ein regelmäßiges Koordinatengitter zu erzeugen, über dem dann eine Funktion von zwei Variablen ausgewertet wird.

In [42]: x, y = np.mgrid[-3:3:100j, -3:3:100j]
   ...: z = (1-x+x**5+y**3)*np.exp(-x**2-y**2)

Um eine Vorstellung vom Verhalten dieser Funktion anhand von Konturlinien zu erhalten, genügt es im einfachsten Fall, die x- und y-Koordinaten des Gitters und die zugehörigen Funktionswerte an die contour-Funktion zu übergeben.

In [43]: contourset = plt.contour(x, y, z)

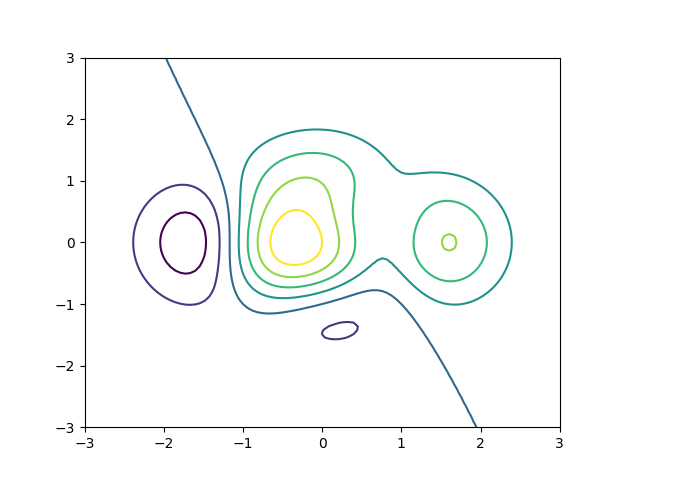
Wenn man jedoch nicht weiß, welche Farbe welchem Wert der Funktion zugeordnet ist, ist so ein Bild häufig nur eingeschränkt nützlich. Es ist daher sinnvoll, jede Konturlinie mit dem zugehörigen Funktionswert zu beschriften. Hierzu haben wir in der vorhergehenden Anweisung bereits die Konturlinien in der Variable contourset gespeichert, mit deren Hilfe wir nun die Beschriftung vornehmen können.

In [44]: plt.clabel(contourset, inline=1)
Out[44]: <a list of 8 text.Text objects>

Ist das Argument inline gleich True oder gleich 1, so wird die Kontur unter der Beschriftung entfernt. Dies ist die Standardeinstellung und müsste daher nicht unbedingt explizit angegeben werden.

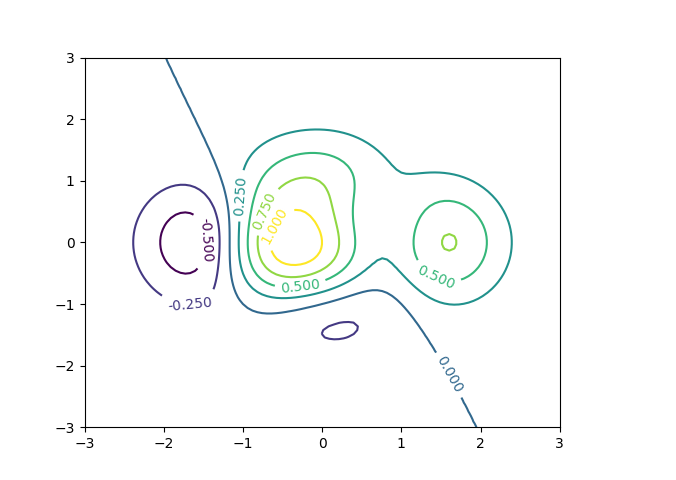
Eine andere Möglichkeit, eine Verbindung zwischen der Farbe der Konturlinien und dem entsprechenden Funktionswert herzustellen, besteht in der Verwendung eines Farbstreifens neben der eigentlichen Abbildung. Im Falle von Konturlinien sind hier nur einzelne Linien bei den entsprechenden Werten zu sehen. Füllt man die Flächen zwischen den Konturlinien, so ist dieser Farbstreifen durchgehend farbig dargestellt, wie wir gleich noch sehen werden.

In [45]: plt.colorbar(contourset)
Out[45]: <matplotlib.colorbar.Colorbar at 0x7f48aeda8a20>

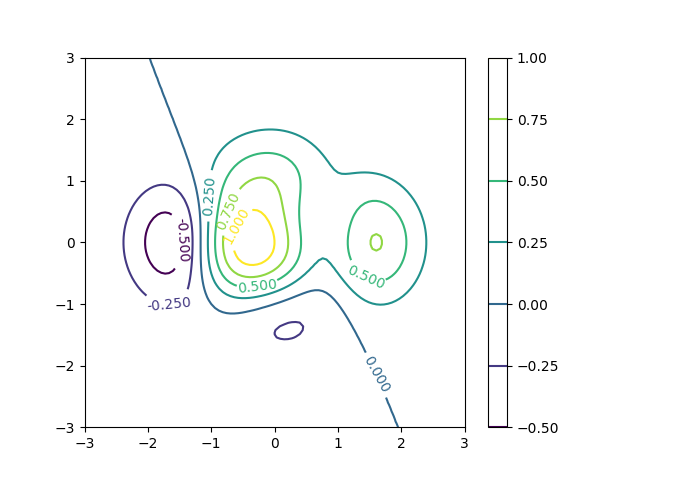
Bis jetzt hatten wir es matplotlib überlassen, die Werte für die einzelnen Konturlinien zu bestimmen. Es ist aber auch möglich, die entsprechenden Werte in einer Liste vorzugeben, wie das nächste Beispiel zeigt.

In [46]: plt.clf()
   ...: contourset = plt.contour(x, y, z, [-0.25, 0, 0.25, 1])
   ...: plt.clabel(contourset, inline=1)
Out[46]: <a list of 4 text.Text objects>

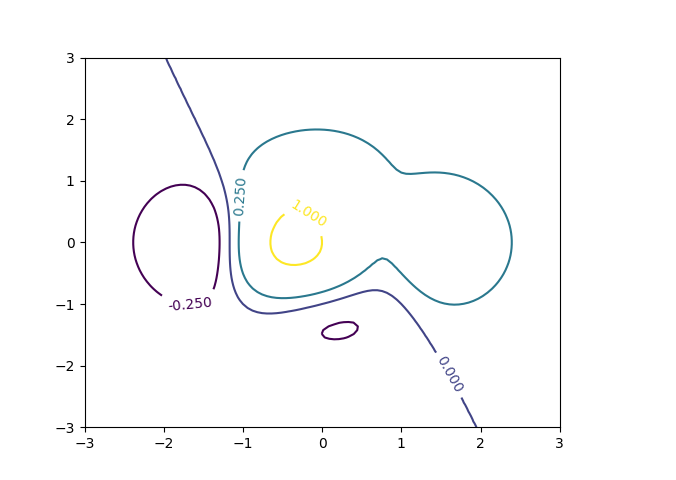
Der Zusammenhang zwischen Funktionswert und Farbe wird durch eine Farbpalette, eine so genannte »color map«, vermittelt. Die bisher verwendete Standardeinstellung läuft unter dem Namen jet. matplotlib stellt eine ganze Reihe verschiedener Farbpaletten zur Verfügung, von denen einige auch gut für Konturplots geeignet sind. Eine Zusammenstellung der Farbpaletten aus der matplotlib-Galerie ist nachfolgend abgebildet.

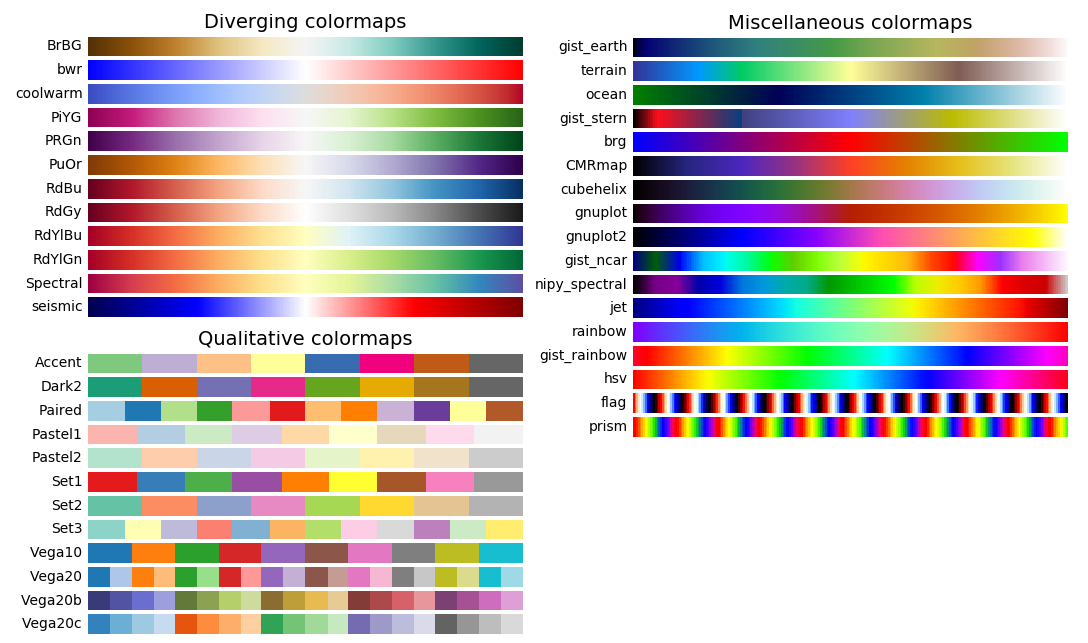
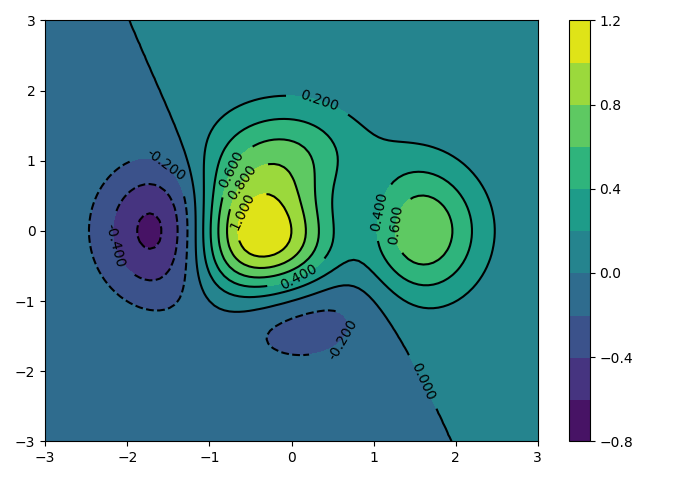
Im folgenden Beispiel wählen wir mit viridis eine der Farbpaletten, deren Helligkeit gleichmäßig variiert und damit auch in einer Schwarz-Weiß-Darstellung eine adäquate Darstellung der Farben liefert. Mit Hilfe der Funktion contourf füllen wir die Flächen zwischen den Konturlinien. Damit die Linien deutlicher sichtbar werden, werden sie in schwarz dargestellt.

In [47]: plt.clf()
   ...: levels = 10
   ...: contourset = plt.contourf(x, y, z, levels, cmap='viridis')
   ...: plt.colorbar(contourset)
   ...: contourlines = plt.contour(x, y, z, levels, colors=('k',))
   ...: plt.clabel(contourlines, inline=1)
Out[47]: <a list of 11 text.Text objects>

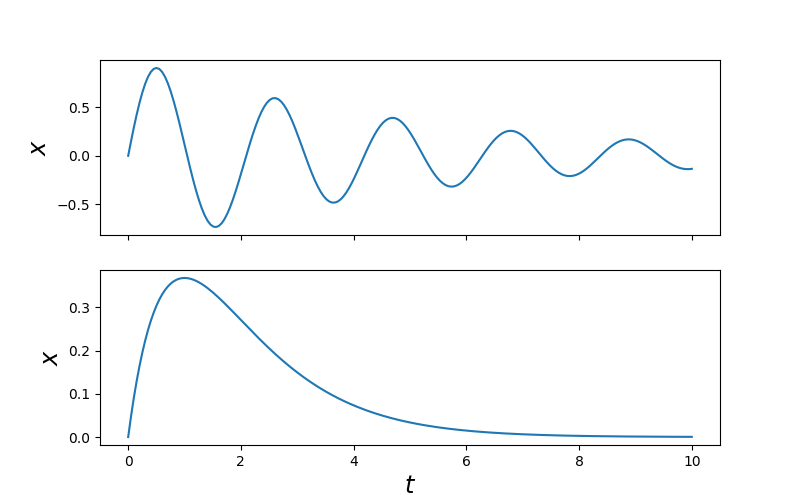
Vor allem bei der Erstellung von Grafiken für Publikationen steht man gelegentlich vor der Aufgabe, mehrere Abbildungen zu einer einzigen Abbildung zusammenzufassen. Man verwendet hierfür die subplots-Funktion, die in den ersten beiden Argumenten die Zahl der Zeilen und der Spalten enthält. Wir wollen zwei Grafiken übereinandersetzen und wählen daher 2 Zeilen und 1 Spalte. Neben der Gesamtgröße der Abbildung geben wir noch an, dass die x-Achse aus der unteren Abbildung auch für die obere Abbildung gelten soll. subplots gibt ein figure-Objekt zurück, das sich auf die ganze Abbildung bezieht sowie in unserem Fall zwei axes-Objekte, die sich jeweils auf die Unterabbildungen beziehen. Hier wird die Unterscheidung zwischen Abbildung und Unterabbildungen deutlich, die weiter oben bereits angedeutet wurde. Nachdem die Unterabbildungen angelegt wurden, können mit Hilfe des entsprechenden axes-Objekts Änderungen an den Unterabbildungen vorgenommen werden. Wir zeichnen hier konkret in jeder Unterabbildung einen Funktionsgraphen und nehmen eine Achsenbeschriftung vor.

In [48]: tvals = np.linspace(0, 10, 200)
   ...: x0vals = np.exp(-0.2*tvals)*np.sin(3*tvals)
   ...: x1vals = tvals*np.exp(-tvals)
   ...: fig, (ax0, ax1) = plt.subplots(2, 1, figsize=(8, 5), sharex=True)
   ...: ax0.plot(tvals, x0vals)
   ...: ax1.plot(tvals, x1vals)
   ...: ax1.set_xlabel('$t$', size='xx-large')
   ...: ax0.set_ylabel('$x$', size='xx-large')
   ...: ax1.set_ylabel('$x$', size='xx-large')
Out[48]: <matplotlib.text.Text at 0x7f48aeb96278>

Mit matplotlib sind auch dreidimensionale Darstellungen möglich, zumindest in einem gewissen Umfang, der für viele Zweck ausreicht. In dem folgenden Beispiel wird eine Funktion zweier Variablen dreidimensional dargestellt. Zusätzlich wird in der x-y-Ebene eine Projektion der Funktionsdaten gezeigt. Dreidimensionale Darstellungen erfordern einen Import aus dem matplotlib Toolkit, der zunächst vorgenommen wird. Anschließend wird die darzustellende Funktion auf einem Gitter ausgewertet. Zudem wählen wir eine Farbpalette, die wir sowohl für die dreidimensionale Darstellung als auch für die Projektion verwenden.

Nachdem wir eine Abbildung unter der Variable fig erzeugt haben, können wir für eine darin enthaltene Unterabbildung ax eine dreidimensionale Projektionsdarstellung festlegen. Anschließend können wir mit Hilfe der zuvor berechneten Funktionsdaten eine dreidimensionale Darstellung der Funktion zeichnen lassen. Die Argumente rstride und cstride geben an, in welchen Abständen bezogen auf die Gitterweite Schnittlinien gezeichnet werden. Das letzte Argument, alpha, betrifft einen Aspekt der Farbdarstellung, den wir bis jetzt noch nicht besprochen hatten. Der Alphakanal gibt zusätzlich beispielsweise zu den Farbkanälen R, G und B die Transparenz der Farbe an. Im Beispiel wird die Oberfläche also teilweise transparent dargestellt.

Die Projektion in die x-y-Ebene stellen wir wie bereits besprochen mit Hilfe der Funktion contourf dar, wobei wir in diesem Beispiel auf die Darstellung von Konturlinien verzichten. Bei der Anwendung in einer dreidimensionalen Darstellung müssen wir noch die Ausrichtung der Projektsebene mit Hilfe der Normalenrichtung zdir und die Lage mit Hilfe von offset spezifizieren. Durch eine entsprechende Wahl von zdir wäre es auch möglich, Projektionen in die x-z- und die y-z-Ebene vorzunehmen.

Abschließend setzen wir in unserem Beispiel die Achsenbeschriftung und erweitern den Wertebereich der z-Achse, um die Projektion darstellen zu können. Zum Schluss wird die Abbildung, die hier im Gegensatz zu den meisten Beispielen dieses Kapitels objektorientiert erstellt wurde, dargestellt.

In [49]: from mpl_toolkits.mplot3d import Axes3D
   ...: x, y = np.mgrid[-3:3:30j, -3:3:30j]
   ...: z = (x**2+y**3)*np.exp(-x**2-y**2)
   ...: cmap = 'coolwarm'
   ...:
   ...: fig = plt.figure()
   ...: ax = fig.gca(projection='3d')
   ...: ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cmap, alpha=0.5)
   ...: cset = ax.contourf(x, y, z, zdir='z', offset=-0.8, cmap=cmap)
   ...: ax.set_xlabel('$x$', size='xx-large')
   ...: ax.set_ylabel('$y$', size='xx-large')
   ...: ax.set_zlabel('$z$', size='xx-large')
   ...: ax.set_zlim(-0.8, 0.5)
   ...:
   ...: plt.draw()

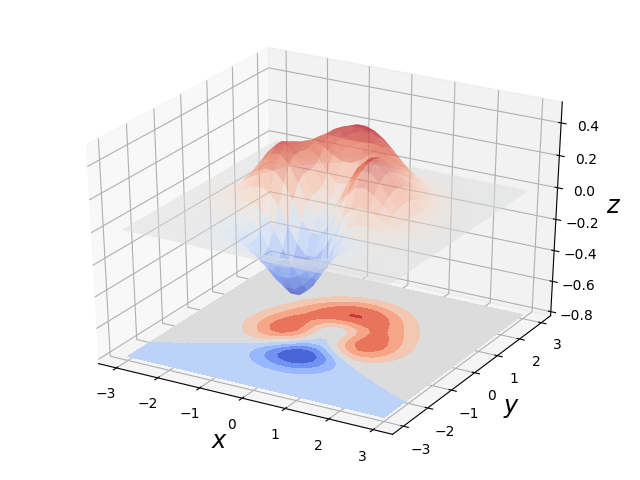
Es sei noch angemerkt, dass sich die dreidimensionale Darstellung im grafischen Benutzerinterface nach Belieben in alle Richtungen drehen lässt, so dass sich bequem eine geeignete Blickrichtung finden lässt, die eine instruktive Sicht auf die dargestellten Daten ermöglicht.

In diesem Kapitel mussten wir uns auf einige für die Anwendung wichtige Problemstellungen konzentrieren und konnten daher keinen vollständigen Überblick über die Möglichkeiten von matplotlib geben. Um einen detaillierteren Einblick zu bekommen, bietet sich ein Blick in die bereits mehrfach erwähnte Beispielgalerie an. Dort ist auch der Code verfügbar, mit dem die in der Galerie gezeigten Beispiele erzeugt wurden. Weitere Informationen über die verfügbaren Funktionen und die jeweiligen Argumente liefert die umfangreiche Dokumentation, die ebenfalls auf der matplotlib-Webseite www.matplotlib.org bereitgestellt ist.

Erstellung von Grafiken mit PyX¶

In diesem Kapitel wollen wir als zweites Paket zur Erzeugung von Abbildungen PyX besprechen. Es handelt sich dabei um ein Paket, das zunächst von André Wobst und Jörg Lehmann während ihrer Doktorandenzeit an der Universität Augsburg entwickelt wurde. Zwischenzeitlich leistete Michael Schindler einige interessante Beiträge, und heute wird PyX von den beiden Erstgenannten weiterentwickelt.

PyX eignet sich im Gegensatz zu dem zuvor besprochenen matplotlib-Paket auch sehr gut zur Erstellung von schematischen Darstellungen. Wir wollen diesen Aspekt daher als erstes besprechen. Anschließend werden wir zeigen, wie in PyX auch grafische Darstellungen von Daten erzeugt werden können. Interessant ist, dass man für beide Anwendungen nur ein einziges Paket benötigt und die beiden Darstellungsarten auch kombinieren kann. Wie schon bei matplotlib würde es zu weit führen, alle Möglichkeiten von PyX zu diskutieren. Wir treffen daher im Folgenden eine Auswahl wichtiger anwendungsrelevanter Aspekte und verweisen ansonsten auf die Dokumentation unter pyx.sf.net sowie die Beispielseiten und die Galerie. Letztere ist derzeit weniger umfangreich als bei matplotlib, was jedoch nichts über den Funktionalitätsumfang aussagt.

Bis zur Version 0.12.1 war PyX nur unter Python 2 lauffähig und seit der Version 0.13 ist es ausschließlich unter Python 3 funktionsfähig. Die installierte Version von PyX kann man folgendermaßen herausfinden:

In [1]: import pyx
   ...: pyx.__version__
Out[1]: '0.13'

Die folgende Diskussion bezieht sich auf die Version 0.13 für Python 3. Zu Beginn eines Pythonskripts wird man zuerst PyX sowie bei Bedarf weitere Pakete importieren. Im Gegensatz zu matplotlib importieren wir alle Module, da die Auswirkung auf den Namensraum wesentlich überschaubarer ist als bei matplotlib. Natürlich kann man sich aber auch darauf beschränken, nur die jeweils benötigten Module zu importieren.

In [2]: from pyx import *

Ein wesentlicher Aspekt bei der Erstellung schematischer Abbildungen ist das Zeichnen von Pfaden, eine eventuelle Dekorierung von Pfaden sowie das Füllen von Flächen, die durch gegebene Pfade begrenzt werden. In PyX erfolgt das Zeichnen grundsätzlich auf einem »canvas«, also einer Leinwand. Wir werden später noch sehen, dass ein Canvas eine sehr flexible Struktur darstellt, die transformiert, also beispielsweise skaliert, gespiegelt oder geschert werden kann. Zudem kann ein Canvas in einen anderen Canvas eingefügt werden. Bei PyX wird man im Allgemeinen sehr früh einen Canvas bereitstellen, um darin zeichnen zu können. In unserem ersten Beispiel definieren wir uns einen Canvas. Diese Klasse ist im canvas-Modul definiert, so dass die Initialisierung mit der ersten Zeile aus dem folgenden Code erfolgt. Der Code in der zweiten Zeile verlangt, dass auf dem gerade definierten Canvas ein Kreis um den Ursprung mit Radius 1 gemalt wird. So lange nichts anderes angegeben wird, wird der Kreis mittels einer schwarzen durchgezogenen Linie mit der Defaultbreite dargestellt.

In [3]: c = canvas.canvas()
   ...: c.stroke(path.circle(0, 0, 1))

Abweichungen von den Defaulteinstellungen kann man in einer Attributliste angeben. Zu beachten ist, dass hier immer eine Liste anzugeben ist, selbst dann, wenn nur ein einziges Attribut neu definiert wird. Mit Hilfe der folgenden Codezeile wird auf dem bereits existierenden Canvas ein weiterer Kreis gemalt, der nun durch eine dickere, gestrichelte Linie dargesellt wird.

In [4]: c.stroke(path.circle(2.2, 0, 1),
   ...:          [style.linestyle.dashed, style.linewidth.THIck])

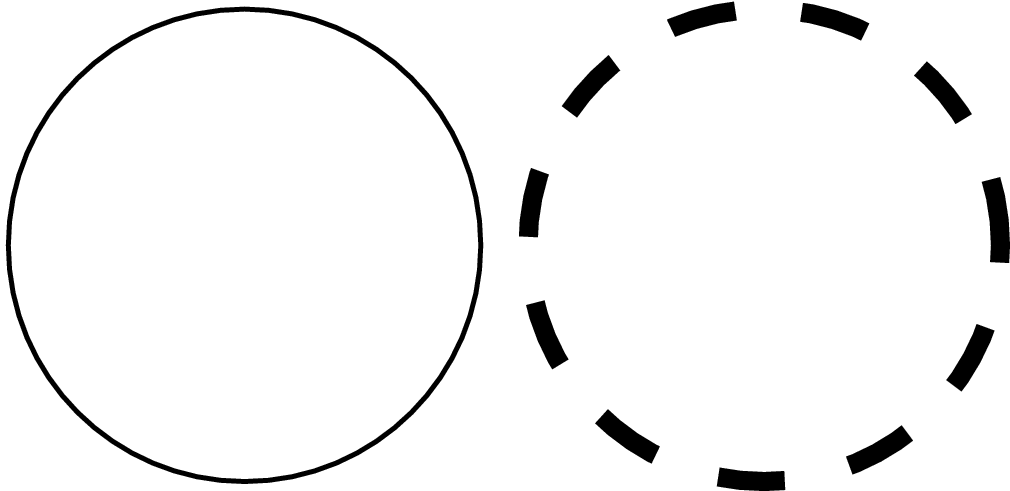
Neben durchgezogenen und gestrichelten Linien gibt es auch punktierte und strichpunktierte Linien, wobei sich die Strichlänge bei Bedarf einstellen lässt. Die Liniendicke wird umso größer, je mehr Buchstaben des Wortes »thick« groß geschrieben werden. Von »THIN« bis »THICK« ändert sich die Linienbreite in Schritten von \(\sqrt{2}\) und umfasst dabei einen Umfang von etwa einem Faktor 45.

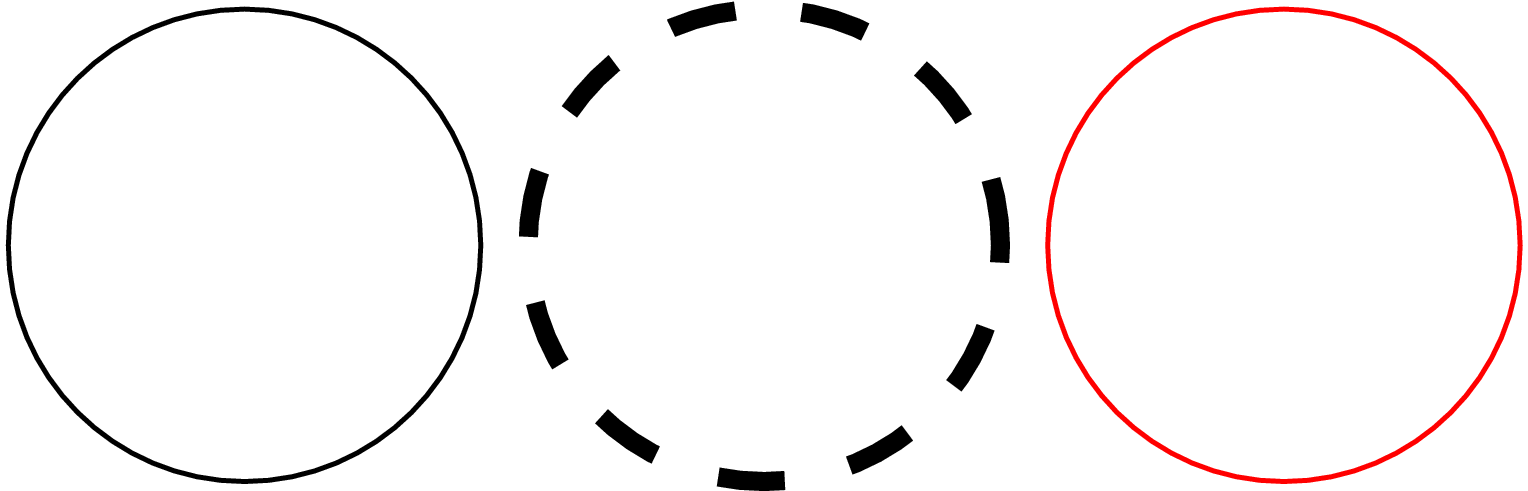
Ein weiterer Parameter beim Malen des Pfades ist die Farbe, die man ganz ähnlich wie bei matplotlib auf verschiedene Weisen festlegen kann. Im rgb-System sind wenige Farben per Namen ansprechbar. Es handelt sich um rot (red), grün (green), blau (blue), weiß (white) und schwarz (black). Eine wesentlich größere Anzahl von Farbnamen ist im cmyk-System definiert, wobei cmyk für Cyan, Magenta, Gelb (Yellow) und Schwarz (blacK) steht. Einen roten Kreis kann man also folgendermaßen erhalten:

In [5]: c.stroke(path.circle(4.4, 0, 1), [color.rgb.red])

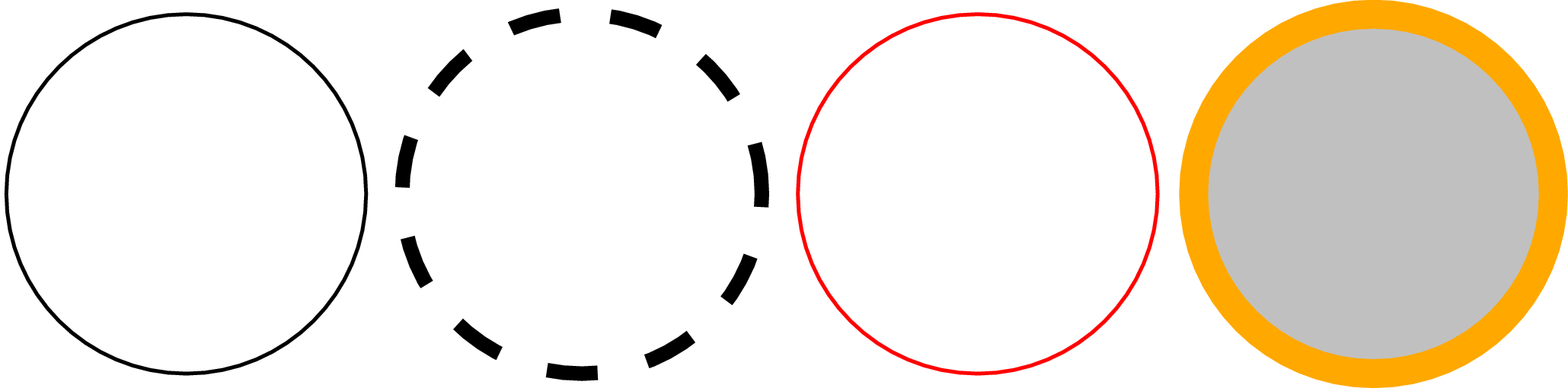
Man kann aber Pfade nicht nur zeichnen, sondern auch füllen. Hierfür gibt es zwei Möglichkeiten, die wir nun ansehen wollen. Man kann den Pfad durch Füllen dekorieren, indem man zu den Attributen deco.filled() hinzufügt. Die Füllung kann man wiederum mit einer Liste von Attributen genauer spezifizieren. In unserem Beispiel wollen wir als Farbe ein helles Grau festlegen. Lässt man in color.grey() das Argument von 0 bis 1 laufen, so erhält man Graustufen zwischen Schwarz und Weiß. Anhand der Linienfarbe demonstriert unser Beispiel auch die Möglichkeit, Farben mit Hilfe des hsb-Systems festzulegen, wobei der »value« in dieser Bezeichnung durch »brightness« ersetzt wurde, ein ebenfalls übliches Akronym für dieses zusätzlich auf dem Farbwert und der Sättigung basierenden Farbsystems.

In [6]: c.stroke(path.circle(6.6, 0, 1),
   ...:          [color.hsb(0.11, 1, 1), style.linewidth.THICK,
   ...:           deco.filled([color.grey(0.7)])])

Ein alternativer Weg, einen gefüllten Kreis zu malen, der vollkommen äquivalent zu dem vorherigen Vorgehen ist, besteht darin, das Füllen des Kreises in den Vordergrund zu stellen. Dabei verwendet man statt der stroke-Methode die fill-Methode. Dabei hat man die Wahl, den Pfad selbst durch Angabe des deco.stroked()-Methode zu malen oder dies nicht zu tun. Das folgende Beispiel unterscheidet sich von dem vorhergehenden lediglich durch die Wahl der Farben, wobei wir hier noch die Verwendung des rgb-Systems demonstrieren, das wir bereits von matplotlib kennen.

In [7]: c.fill(path.circle(8.8, 0, 1), [color.rgb(1, 0.5, 0.5),
   ...:         deco.stroked([style.linewidth.THICK, color.rgb(0.5, 0.5, 1)])])

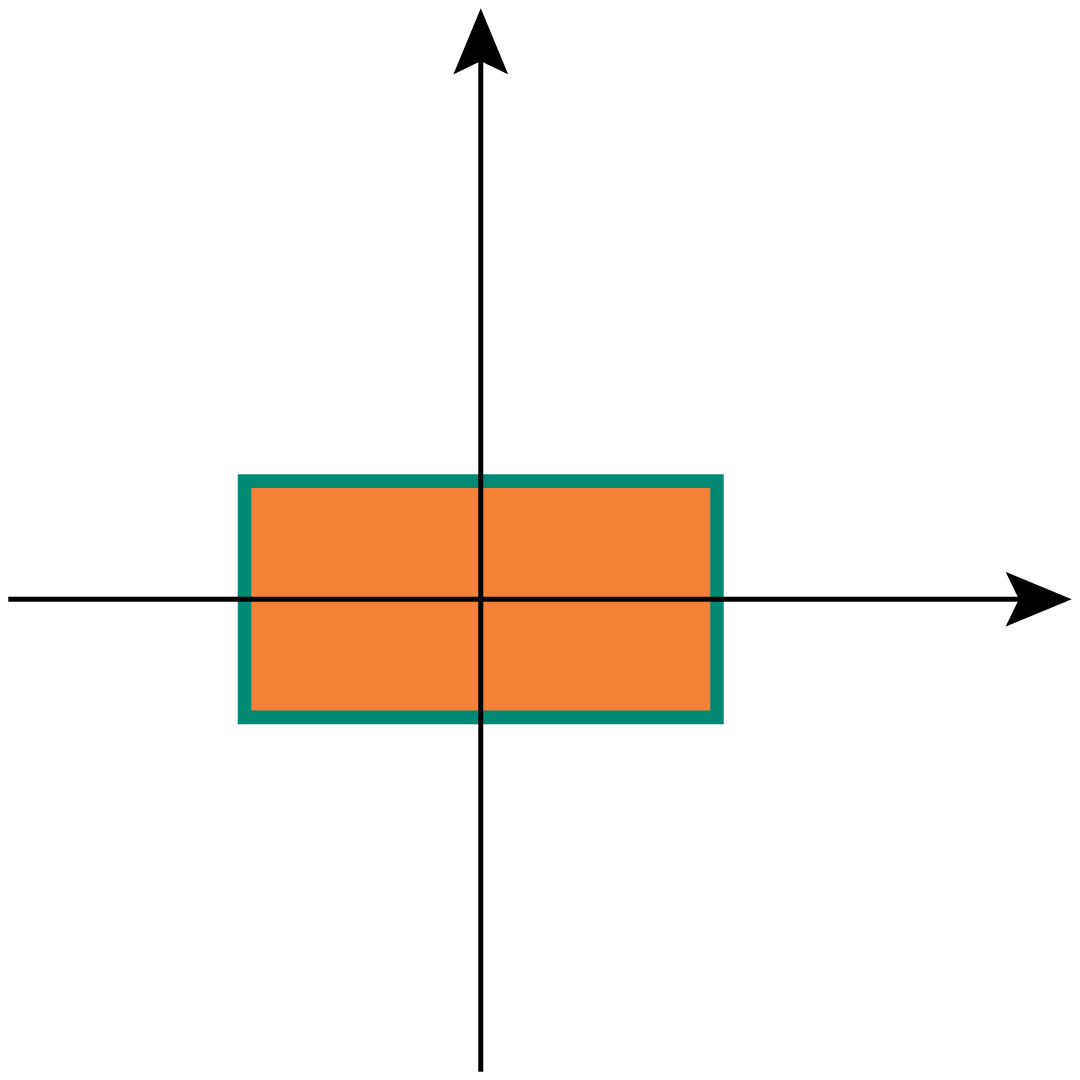
Selbstverständlich stehen als Pfade nicht nur Kreise zur Verfügung. Im folgenden Beispiel finden zwei weitere Pfade Verwendung, nämlich Linien (path.line) und Rechtecke (path.rect). Im ersten Fall sind die x- und y-Koordinate von Anfangs- und Endpunkt anzugeben, während im zweiten Fall die ersten beiden Argumente einen Eckpunkt angeben und die beiden folgenden Punkte die Breite und die Höhe des Rechtecks spezifizieren.

Zusätzlich zu diesen Pfaden demonstriert das Beispiel noch eine weitere Pfaddekoration, nämlich das Platzieren von Pfeilen am Anfang (barrow) und/oder Ende (earrow) eines Pfades. Dabei lässt sich die Größe des Pfeils festlegen. Hier verlangen wir mit large Pfeile, die etwas größer als die Defaultpfeile sind. Mit Hilfe von Großbuchstaben lässt sich die Pfeilgröße weiter erhöhen, ähnlich wie dies bei der Linienbreite der Fall war. Kleinere Pfeile erhält man mit Hilfe von small. Schließlich demonstriert das Beispiel die Verwendung von benannten Farben im cmyk-System, das oben schon kurz erläutert wurde.

In [8]: c = canvas.canvas()
   ...: c.fill(path.rect(-1, -0.5, 2, 1),
   ...:        [color.cmyk.Orange, deco.stroked([color.cmyk.PineGreen,
   ...:                                          style.linewidth.THick])])
   ...: c.stroke(path.line(-2, 0, 2.5, 0), [deco.earrow.large])
   ...: c.stroke(path.line(0, 2.5, 0, -2), [deco.barrow.large])

Neben der Verwendung vordefinierter Pfade erlaubt es PyX auch, Pfade aus mehreren Pfadsegmenten zu bilden. Im folgenden Beispiel wird ein Pfad aus vier geraden Linien zusammengesetzt. Zunächst wird mit path.moveto() ein Startpunkt gewählt, der hier im Koordinatenursprung liegt. Von diesem Punkt ausgehend wird dann eine Linie zu einem weiteren Punkt gezogen, der in absoluten Koordinaten angegeben wird und als nächster Ausgangspunkt dient. Auf diese Weise wird hier ein Pfad konstruiert, der ein Quadrat beschreibt.

Obwohl der Pfad schließlich an den Ausgangspunkt zurückkehrt, handelt es sich nicht um einen geschlossenen Pfad. Dies wird deutlich, wenn man die Linienbreite sehr groß wählt, wie es hier der Fall ist. Die Funktionsweise von wscale und weiteren Längenskalen wird etwas weiter unten genauer besprochen. Die letzte Zeile in dem folgenden Beispiel führt zwar dazu, dass der eingangs definierte Pfad p gezeichnet wird, aber die Linie ist offenbar nicht geschlossen.

In [9]: p = path.path(path.moveto(0, 0),
   ...:               path.lineto(2, 0),
   ...:               path.lineto(2, 2),
   ...:               path.lineto(0, 2),
   ...:               path.lineto(0, 0))
   ...: unit.set(wscale=40)
   ...: c = canvas.canvas()
   ...: c.stroke(p)

Das Schließen eines Pfades erreicht man durch Anhängen von path.closepath(), wobei es nicht einmal notwendig ist, zum Ausgangspunkt zurückzukehren. closepath fügt bei Bedarf selbstständig das fehlende Liniensegment zum Ausgangspunkt des Pfades ein. Die Quadratkontur wird jetzt vollständig dargestellt.

In [10]: p = path.path(path.moveto(0, 0),
   ...:               path.lineto(2, 0),
   ...:               path.lineto(2, 2),
   ...:               path.lineto(0, 2),
   ...:               path.closepath())
   ...: c = canvas.canvas()
   ...: c.stroke(p)

Für die folgenden Beispiele stellen wir die stark erhöhte Linienbreite zunächst einmal wieder auf die Defaultbreite zurück.

In [11]: unit.set(wscale=1)

In den beiden vorhergehenden Beispielen haben wir die Pfadsegmente mit Hilfe von absoluten Koordinaten festgelegt. Statt lineto kann man aber auch rlineto verwenden, in dem eine Linie relativ zum aktuellen Endpunkt des Pfades angegeben wird. Das folgende Beispiel demonstriert dies anhand der Simulation einer Zufallsbewegung, bei der in jedem Schritt um einen festen Abstand in eine zufällige Richtung weitergegangen wird.

In [12]: from numpy import random
   ...: from math import pi, cos, sin
   ...:
   ...: directions = 2*pi*random.random(1000)
   ...: pathelems = [path.rlineto(0.1*cos(dir), 0.1*sin(dir)) for dir in directions]
   ...: p = path.path(path.moveto(0, 0), *pathelems)
   ...:
   ...: c = canvas.canvas()
   ...: c.stroke(p)

Neben Geraden kann man auch Kreissegmente verwenden, um Pfade zu konstruieren. Dies wird hier an einer stadionförmigen Kontur gezeigt.

In [13]: p = path.path(path.moveto(-1, -1), path.lineto(1, -1),
   ...:                path.arc(1, 0, 1, 270, 90), path.lineto(-1, 1),
   ...:                path.arc(-1, 0, 1, 90, 270), path.closepath())
   ...: c = canvas.canvas()
   ...: c.stroke(p, [deco.filled([color.rgb(1, 0.5, 0.5)])])

Zu Beginn hatten wir bereits darauf hingewiesen, dass es die Möglichkeit gibt, einen Canvas zu transformieren. Dabei müssen die Objekte im Canvas transformiert werden, also letztendlich die Pfade. Es ist auch möglich, Pfade vor dem Zeichnen einer Transformation zu unterwerfen, wie wir anhand einiger Beispiel demonstrieren wollen.

Aus dem vordefinierten Kreispfad lassen sich sehr einfach auch Ellipsen erzeugen, indem man die Skalierungstransformation anwendet und dabei unterschiedliche Skalierungsfaktoren in x- und y-Richtung verwendet. Das folgende Beispiel zeigt eine Reihe von Ellipsen mit unterschiedlicher Exzentrizität.

In [14]: p = path.circle(0, 0, 1)
   ...: ncircs = 5
   ...: c = canvas.canvas()
   ...: for n in range(ncircs):
   ...:     c.stroke(p, [trafo.scale(n+1, 1/(n+1)), color.hsb(1, 1, n/(ncircs-1))])

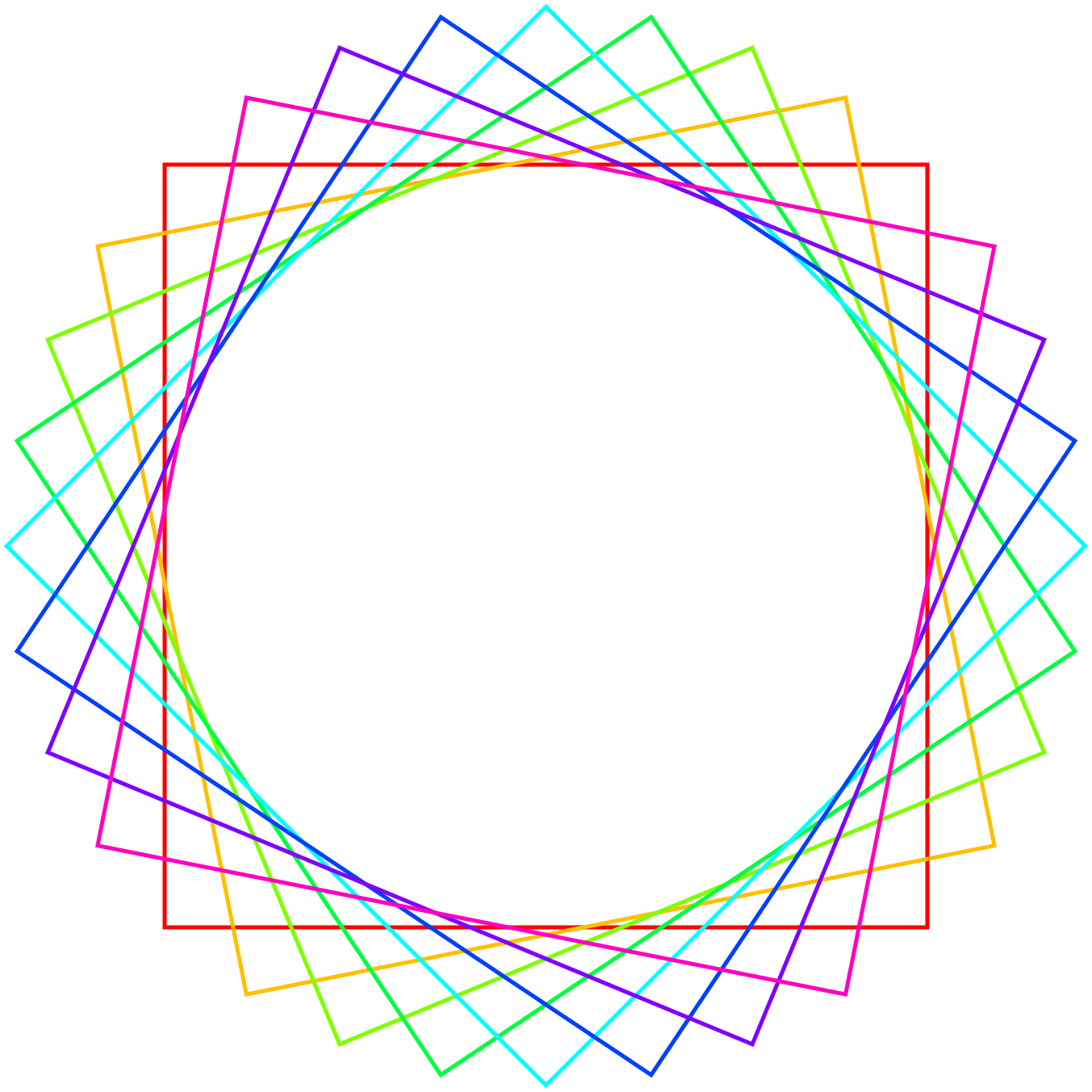
Will man die Hauptachsen der Ellipse nicht in Richtung der Koordinatenachsen legen, so kann man die Ellipse anschließend rotieren. Wir zeigen das Rotieren von Pfaden am Beispiel eines Quadrats, dessen Mittelpunkt im Ursprung liegt. Da die Rotation immer um den Ursprung herum erfolgt, wird das Quadrat um seinen Mittelpunkt gedreht.

In [15]: p = path.rect(-2, -2, 4, 4)
   ...: nrects = 8
   ...: c = canvas.canvas()
   ...: for n in range(nrects):
   ...:     c.stroke(p, [trafo.rotate(90*n/nrects), color.hsb(n/nrects, 1, 1)])

Möchte man stattdessen das Quadrat beispielsweise um seine linke untere Ecke drehen, so muss man diese Ecke zunächst in den Ursprung verschieben, um dann die Drehung durchzuführen. Anschließend erfolgt die Rückverschiebung an die ursprüngliche Position oder, wie in diesem Beispiel, an eine verschobene Position rechts neben der bereits existierenden Abbildung.

In [16]: for n in range(nrects):
   ...:     c.stroke(p, [trafo.translate(2, 2).rotated(
                         90*n/nrects).translated(8, -2),
                         color.hsb(n/nrects, 1, 1)])

Dieses Beispiel zeigt die Hintereinanderausführung von Transformationen, wobei die Transformationen von links nach rechts abgearbeitet werden. Außerdem ist zu beachten, dass die erste Verschiebung hier mit translate aufgerufen wird, während die zweite sowie eventuell noch weiter folgende Verschiebungen mit translated aufgerufen werden. Entsprechend ist in dem obigen Beispiel auch statt rotate die Methode rotated zu verwenden.

Neben Verschiebungen, Skalierungen und Drehungen stehen in PyX auch noch Scherungen (slant) und Spiegelungen (mirror) zur Verfügung. Das folgende Beispiel zeigt, wie man aus einem einzigen Liniensegment durch Drehung und Spiegelung einen sternförmigen Pfad erzeugen kann. Das Argument der mirror-Methode gibt dabei den Winkel an, unter der die Spiegelachse durch den Ursprung verläuft.

In [17]: nstar = 7
   ...: alpha = 360/nstar
   ...: p = path.line(1, 0, 2*cos(pi*alpha/360), 2*sin(pi*alpha/360))
   ...: c = canvas.canvas()
   ...: for n in range(nstar):
   ...:     c.stroke(p.transformed(trafo.rotate(alpha*n)))
   ...:     c.stroke(p.transformed(trafo.mirror(alpha/2).rotated(alpha*n)))

Gelegentlich ist es nützlich, Schnittpunkte von zwei Pfaden oder Pfadsegmente zwischen zwei vorgegebenen Schnittpunkten zur Verfügung zu haben. Zur Veranschaulichung zeichnen wir zunächst die beiden Pfade, die geschnitten werden sollen. Das sind hier ein Kreis und ein Rechteck.

In [18]: c = canvas.canvas()
   ...: p1 = path.circle(0, 0, 1)
   ...: p2 = path.rect(-3, -0.5, 6, 1)
   ...: c.stroke(p1)
   ...: c.stroke(p2)

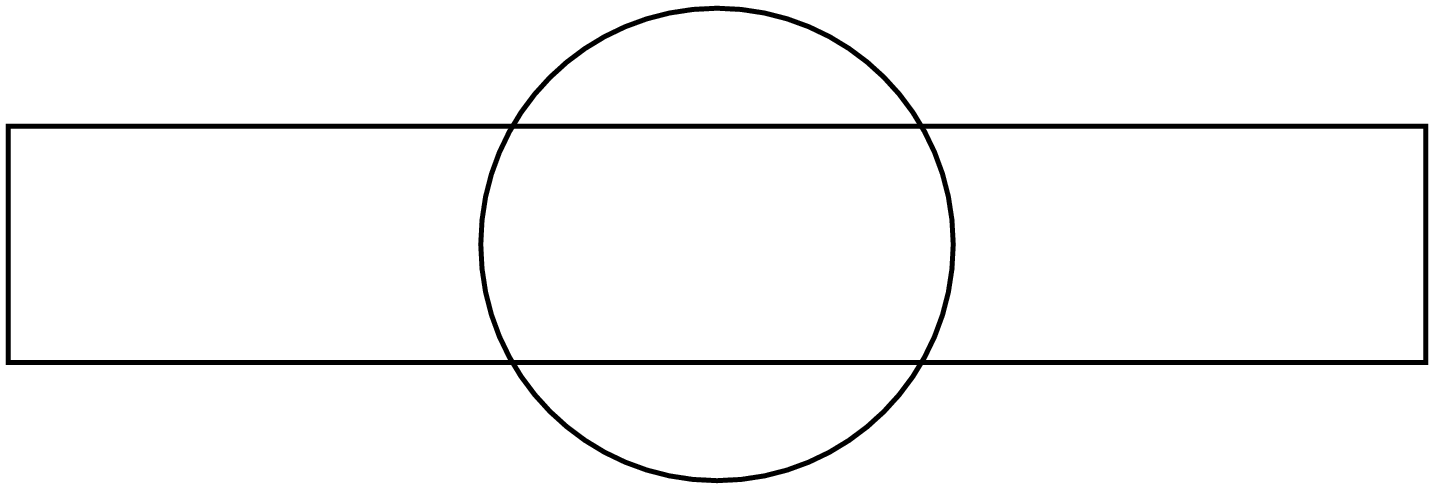
In der ersten Zeile des folgenden Codes wird der Pfad p1, also der Kreis, mit dem Pfad p2, dem Rechteck, geschnitten. Dabei werden zwei Tupel, hier intersect_circle und intersect_rect genannt, erzeugt, die entsprechend den vier Schnittpunkten jeweils vier Werte enthalten, die in einer Parametrisierung der Pfade die Schnittpunkte angeben. In der zweiten und dritten Zeile werden die beiden Pfade an den Schnittpunkten aufgetrennt, so dass zweimal vier Teilpfade entstehen. Diese werden anschließend so zusammengefügt, dass am Ende der Schnittbereich der beiden Pfade farbig gefüllt werden kann.

In [19]: intersect_circle, intersect_rect = p1.intersect(p2)
   ...: circle_subpaths = p1.split(intersect_circle)
   ...: rect_subpaths = p2.split(intersect_rect)
   ...: p = (circle_subpaths[0] << rect_subpaths[1]
   ...:      << circle_subpaths[2] << rect_subpaths[3])
   ...: c.fill(p, [color.rgb.red])

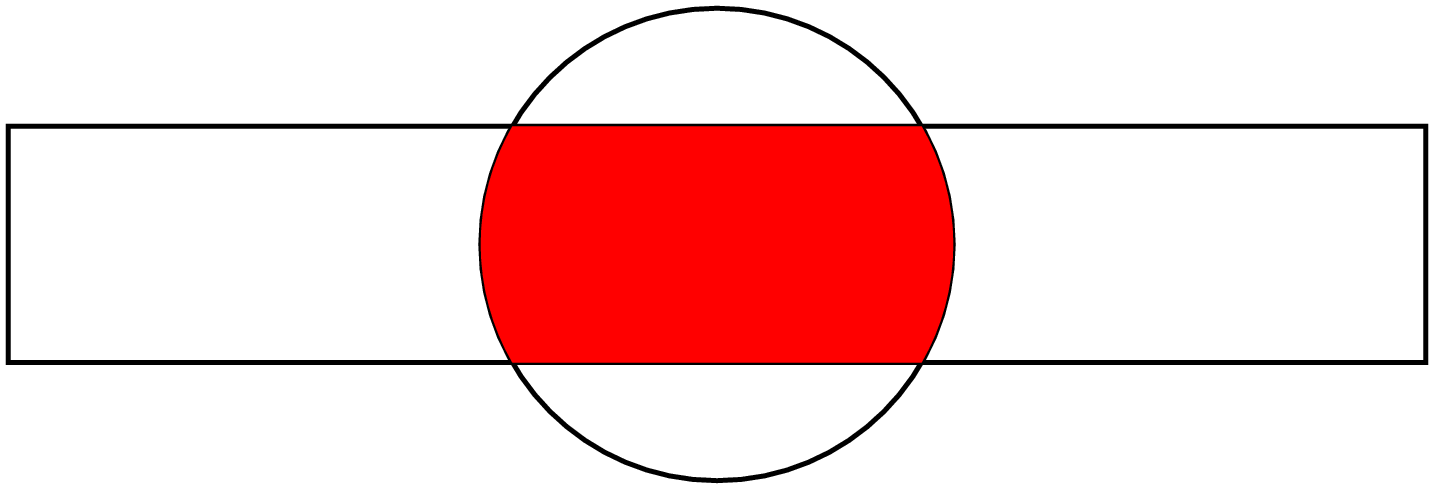
Bei komplizierteren Pfaden ist es unter Umständen nicht ganz einfach, die Tangenten- oder Normalenrichtung zu bestimmen. In solchen Fällen kann man sich von PyX helfen lassen. Zur Illustration konstruieren wir zunächst eine kubische Bézierkurve, die durch vier Punkte charakterisiert ist. Dabei handelt es sich um eine kubische Kurve, für die der erste und vierte Punkt den Anfangs- und den Endpunkt festlegen. Die Verbindungslinien vom ersten zum zweiten sowie vom dritten zum vierten Punkt bestimmen zudem die Kurvensteigung im Anfangs- und Endpunkt, wie im Beispiel durch die blauen Geraden dargestellt ist.

In [20]: x = (0, 3, 6, 6)
   ...: y = (0, 3, 3, 0)
   ...: p = path.curve(x[0], y[0], x[1], y[1], x[2], y[2], x[3], y[3])
   ...: c = canvas.canvas()
   ...: c.stroke(p)
   ...: for xc, yc in zip(x, y):
   ...:     c.fill(path.circle(xc, yc, 0.1), [color.rgb.blue])
   ...: c.stroke(path.line(x[0], y[0], x[1], y[1]), [color.rgb.blue])
   ...: c.stroke(path.line(x[2], y[2], x[3], y[3]), [color.rgb.blue])

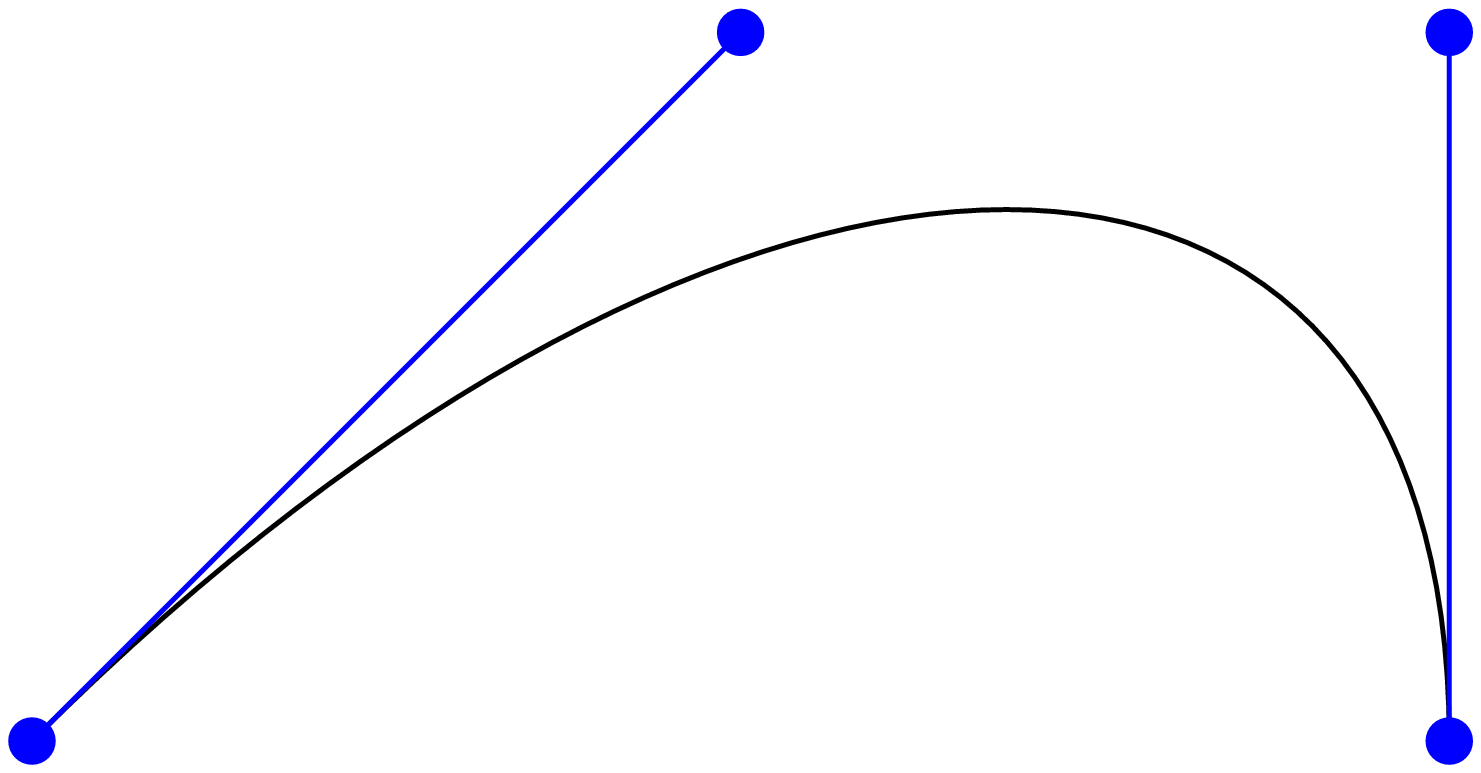
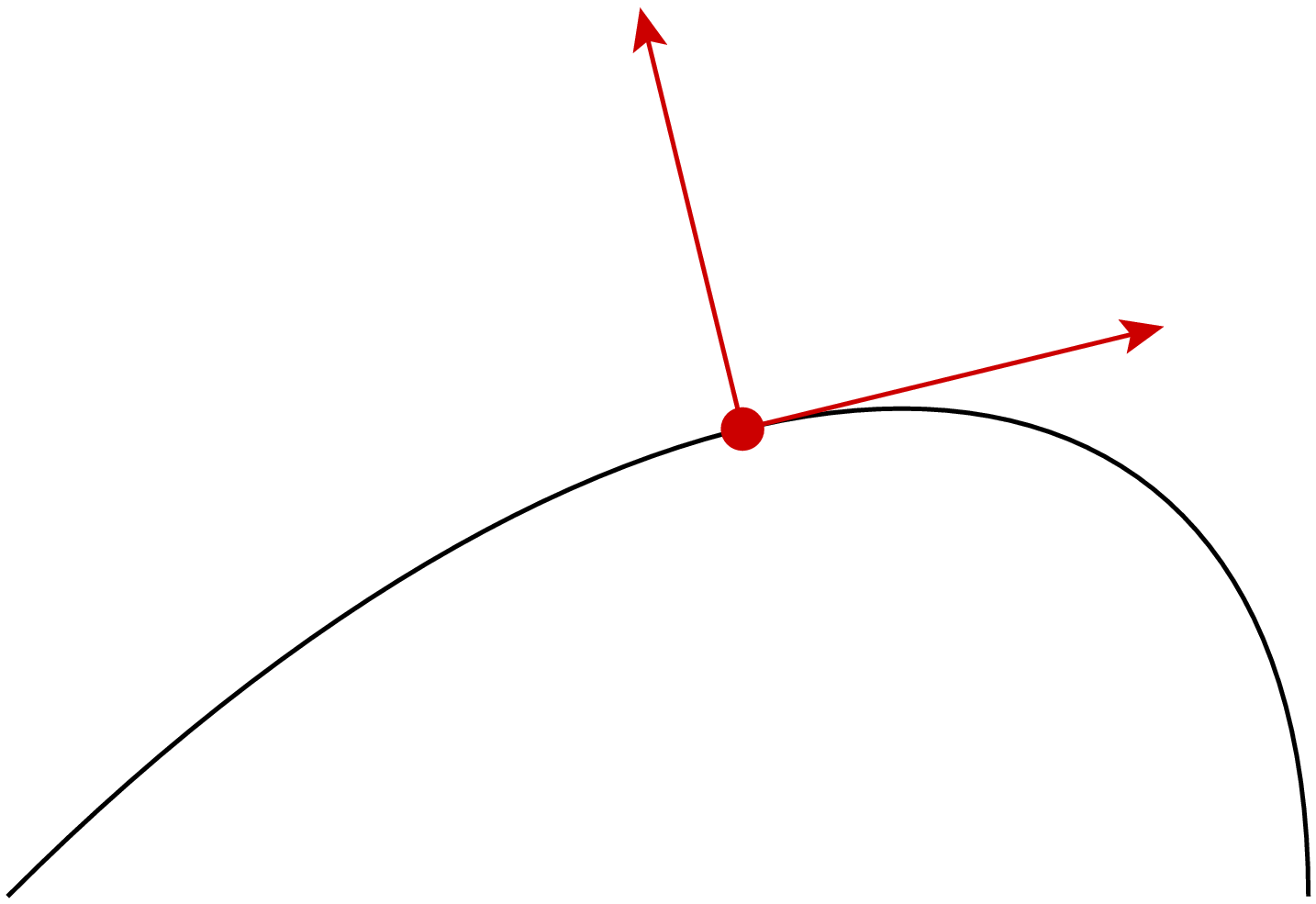
Im folgenden Beispiel soll bei der Hälfte der Kurve der Tangenten- und der Normalenvektor eingezeichnet werden. Dazu wird in der dritten Zeile zunächst mit p.arclen() die Länge des Pfads p bestimmt und dann mittels p.arclentoparam() der Parameter berechnet, der der Hälfte der Pfadlänge entspricht. An diesem Punkt kann man dann mit p.tangent() ein Geradenstück mit vorgegebener Länge in Tangentialrichtung erzeugen, das hier mit einem Pfeil am Ende gezeichnet wird. Um den Normalenvektor zu zeichnen, wird der Tangentialvektor einfach um 90° im Gegenuhrzeigersinn gedreht. Dabei ist allerdings zu beachten, dass der Vektor zunächst in den Ursprung verschoben, dort gedreht, und anschließend wieder in den Ausgangspunkt zurückverschoben werden muss.

In [21]: c = canvas.canvas()
   ...: c.stroke(p)
   ...: paramhalf = p.arclentoparam(0.5*p.arclen())
   ...: x, y = p.at(paramhalf)
   ...: mycolor = color.rgb(0.8, 0, 0)
   ...: c.fill(path.circle(x, y, 0.1), [mycolor])
   ...: c.stroke(p.tangent(paramhalf, length=2), [deco.earrow, mycolor])
   ...: c.stroke(p.tangent(paramhalf, length=2), [deco.earrow, mycolor,
   ...:                 trafo.translate(-x, -y).rotated(90).translated(x, y)])

PyX bietet auch die Möglichkeit, mit Hilfe von Pfaden aus einem Canvas einen Teil herauszuschneiden. Zunächst zeigen wir den vollständigen Canvas, der eine matrixförmige Anordnung von gefärbten Quadraten im hsb-System enthält.

In [22]: c = canvas.canvas()
   ...: for nx in range(10):
   ...:     for ny in range(10):
   ...:         c.fill(path.rect(nx, ny, 1, 1), [color.hsb(nx/9, 1, ny/9)])

Nun legen wir beim Initialisieren des Canvas einen so genannten »clipping path« fest, in unserem Fall einen Kreis, der die Darstellung des Canvas auf das Innere dieses Pfads begrenzt. Damit wird innerhalb des Kreises der entsprechende Ausschnitt aus der zuvor dargestellten Farbmatrix gezeigt.

In [23]: c = canvas.canvas([canvas.clip(path.circle(4, 7, 2))])
   ...: for nx in range(10):
   ...:     for ny in range(10):
   ...:         c.fill(path.rect(nx, ny, 1, 1), [color.hsb(nx/9, 1, ny/9)])

Text ist ein wichtiger Bestandteil von grafischen Darstellungen, ganz gleich ob in Schemazeichnungen oder in Graphen. PyX überträgt die Aufgabe des Textsatzes an TeX oder LaTeX, woher auch das X im Namen des Pakets stammt. Damit bietet PyX die Möglichkeit, Grafiken mit komplexen Texten, bei Bedarf auch ganzen Paragraphen zu versehen. So ist es zum Beispiel möglich, Poster mit Hilfe von PyX zu gestalten. Im Folgenden werden wir einige grundlegende Aspekte von Text in PyX betrachten.

Im folgenden Beispiel wird zunächst ein Achsenkreuz am Ursprung gezeichnet, das hier lediglich zur Orientierung dienen soll. Von Bedeutung ist vor allem die letzte Zeile, in der der Text mit Hilfe der text-Methode gesetzt wird. Die ersten beiden Argumente geben den Punkt an, an dem der Text gesetzt wird, hier also der Koordinatenursprung. Das dritte Argument enthält den Text, der hier zunächst in einer Variable gespeichert wurde. Wie wir weiter unten noch sehen werden, kann dieser Text beispielsweise auch Mathematikanteile entsprechend der TeX- oder LaTeX-Syntax enthalten. Abschließend folgt eine Liste von Attributen. In diesem Fall wird lediglich dafür gesorgt, das der Text etwas größer dargestellt wird. Die möglichen Größenattribute folgen dabei der Vorgabe von TeX wo in aufsteigender Größe die Einstellungen tiny, scriptsize, footnotesize, small, normalsize, large, Large, LARGE, huge und Huge definiert sind. Wie an der Ausgabe zu sehen ist, wird der Text mit dem linken Ende der Basislinie an dem im text-Aufruf angegebenen Punkt positioniert.

In [24]: c = canvas.canvas()
   ...: mytext = 'Augsburg'
   ...: mycolor = color.grey(0.7)
   ...: c.stroke(path.line(-1, 0, 1, 0), [mycolor])
   ...: c.stroke(path.line(0, -1, 0, 1), [mycolor])
   ...: c.text(0, 0, mytext, [text.size.huge])

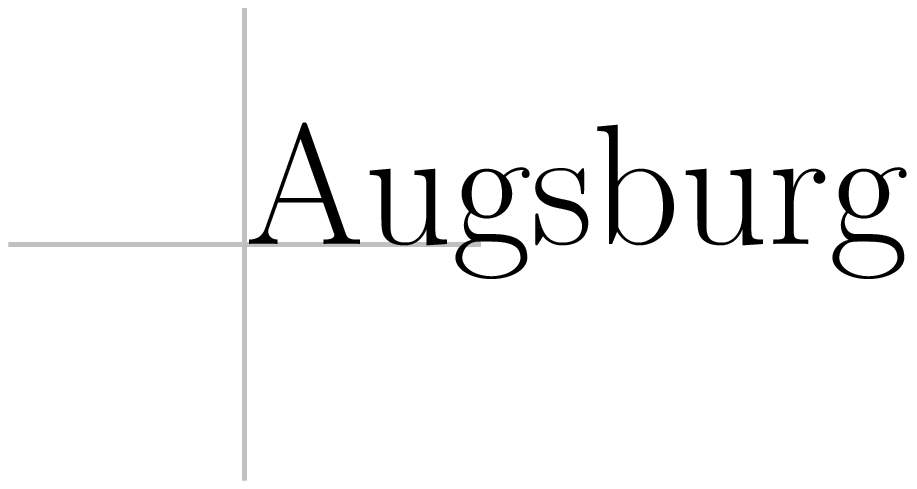
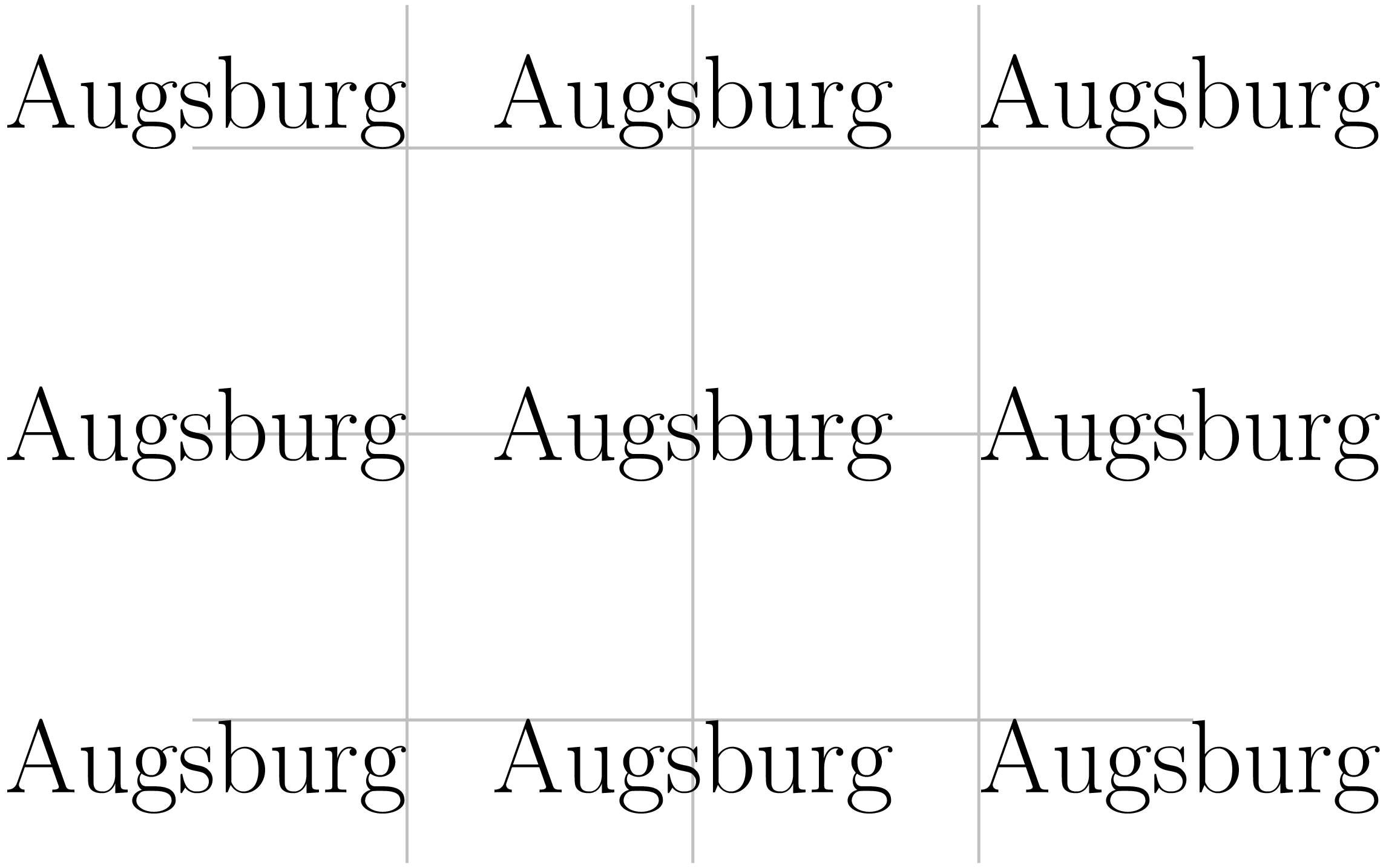
Die Attributliste von text kann neben der Größenabgabe vor allem auch Angaben zur Positionierung des Textes relativ zum angegebenen Referenzpunkt enthalten. Im nächsten Beispiel werden jeweils drei wichtige Varianten der horizontalen und vertikalen Positionierung dargestellt. halign.right, halign.center und halign.left sorgen dafür, dass der Referenzpunkt rechts vom Text, in dessen Mitte oder links vom Text liegt. Die vertikale Positionierung mit valign.top, valign.middle und valign.bottom führt dazu, dass der Referenzpunkt am oberen Ende, in der Mitte bzw. am unteren Ende des den Text umschließenden Rahmens liegt. Auf diese Weise sind sehr flexible Positionierungen möglich.

In [25]: c = canvas.canvas()
   ...: mytext = 'Augsburg'
   ...: mycolor = color.grey(0.7)
   ...: for nx in range(3):
   ...:     c.stroke(path.line(2*nx, 0, 2*nx, 6), [mycolor])
   ...: for ny in range(3):
   ...:     c.stroke(path.line(-1.5, 2*ny+1, 5.5, 2*ny+1), [mycolor])
   ...: for nx, xpos in enumerate((text.halign.right,
   ...:                            text.halign.center,
   ...:                            text.halign.left)):
   ...:     for ny, ypos in enumerate((text.valign.top,
   ...:                                text.valign.middle,
   ...:                                text.valign.bottom)):
   ...:         c.text(2*nx, 2*ny+1, mytext, [xpos, ypos, text.size.huge])

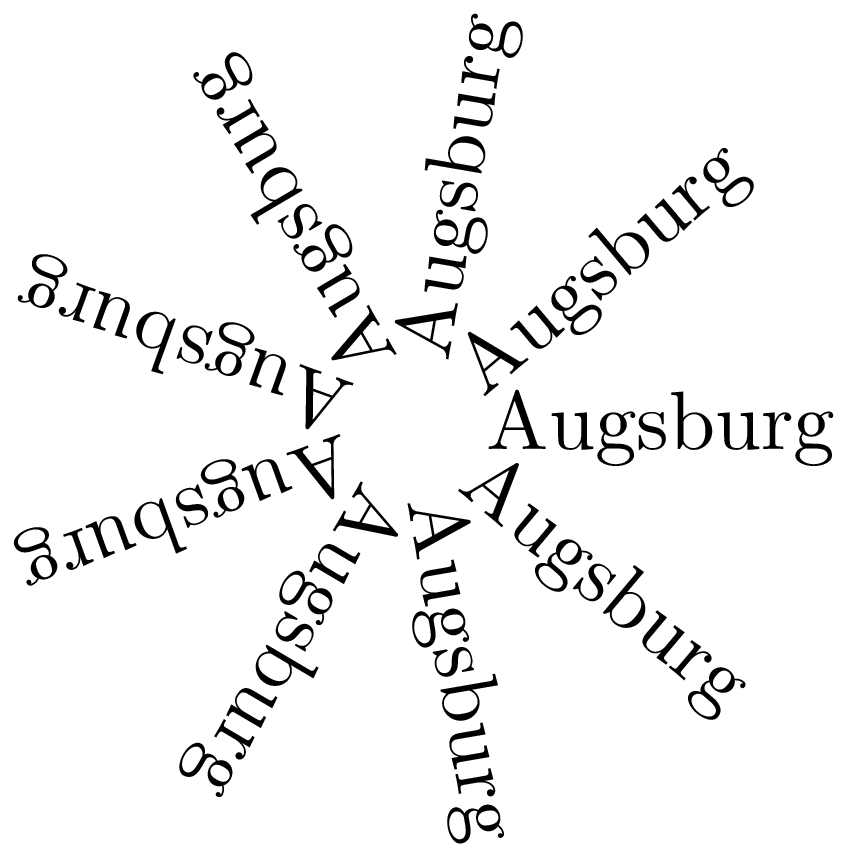
Natürlich können Texte auch transformiert werden, wie wir hier anhand der Drehung des Textes illustrieren. Dabei wird der Text zunächst aus dem Ursprung, der als Drehpunkt fungiert, etwas herausgerückt.

In [26]: c = canvas.canvas()
   ...: for n in range(9):
   ...:     c.text(0, 0, mytext, [text.valign.middle,
                                  trafo.translate(0.3, 0).rotated(40*n)])

Wie bereits erwähnt, unterstützt PyX sowohl den Textsatz mit TeX als auch mit LaTeX. Letzteres basiert auf TeX und stellt Funktionalität zur Verfügung, die den Textsatz erleichtert. In LaTeX kann man die TeX-Syntax verwenden, aber umgekehrt wird spezifische LaTeX-Syntax nicht von TeX verstanden. Daher sollte man sich zunächst überlegen, welche Syntax man verwenden möchte. Defaultmäßig ist TeX voreingestellt, das auch explizit mit Hilfe von text.set(text.TexRunner) verlangt werden kann. LaTeX wählt man mit Hilfe von text.set(text.LatexRunner) aus. Die folgenden beiden Beispiele sind äquivalent. Allerdings wird im ersten Beispiel die TeX-Syntax für einen Bruch benutzt, während im zweiten Beispiel die LaTeX-Syntax verwendet wird.

In [27]: text.set(text.TexRunner)
   ...: c = canvas.canvas()
   ...: c.text(0, 0, '$x = {1\over2}$')

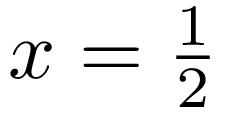
In [28]: text.set(text.LatexRunner)
   ...: c = canvas.canvas()
   ...: c.text(0, 0, r'$x = \frac{1}{2}$')

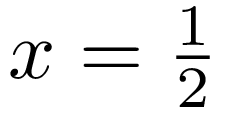
Das letzte Textbeispiel zeigt, wie in LaTeX eine etwas komplexere mathematische Formel gesetzt werden kann. Außerdem ist in der letzten Zeile zu sehen, wie man die Textgröße ohne Verwendung der auf TeX zurückgehenden Schlüsselworte bei Bedarf stufenlos einstellen kann.

In [29]: c = canvas.canvas()
   ...: formula = r'$\displaystyle m\ddot{\vec r} = -\gamma\frac{Mm}{r^3}\vec r$'
   ...: c.text(0, 0, formula, [text.size(2)])

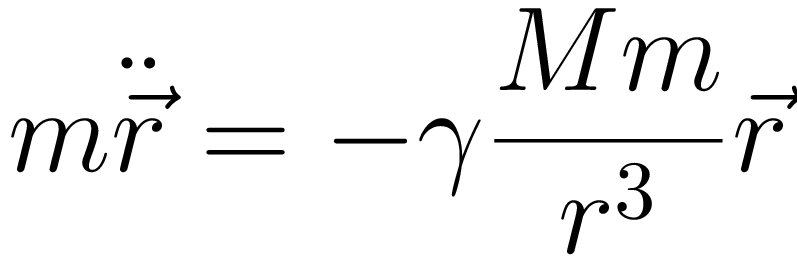
Wir haben in verschiedenen Beispielen immer wieder Längen explizit festgelegt, zum Beispiel die Textgröße, die Linienbreite oder die Pfeilgröße. PyX stellt jedoch auch die Möglichkeit zur Verfügung, Längenskalen global zu definieren. Dabei wird Wert darauf gelegt, visuell unterschiedliche Längen auch unabhängig voneinander verändern zu können. So gibt es uscale, vscale, wscale und xscale, die wir jetzt ausgehend von einer Referenzabbildung, in der alle Skalen auf Eins gesetzt sind, verändern wollen, um ihre Auswirkung vorzustellen.

In [30]: def testfigure():
   ...:     c = canvas.canvas()
   ...:     c.stroke(path.path(path.moveto(2, 0), path.lineto(0, 0),
   ...:              path.lineto(0, 2)), [deco.barrow, deco.earrow])
   ...:     c.fill(path.circle(1, 1, 0.1), [color.rgb.red])
   ...:     c.text(2, 0.2, '$x$', [text.halign.right])
   ...:     c.text(0.2, 2, '$y$', [text.valign.top])
   ...:     return c

In [31]: unit.set(uscale=1, vscale=1, wscale=1, xscale=1)
   ...: testfigure()

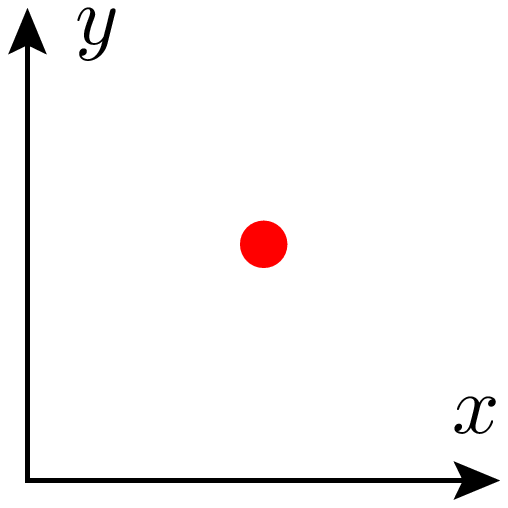
Zunächst verändern wir den Wert von uscale, wodurch Distanzen verändert werden. Dies betrifft in unserer Testabbildung die Länge der Achsen und die Größe der roten Kreisfläche. Unverändert bleiben die Linienbreite der Achsen, die Pfeilgröße sowie die Schriftgröße. Allerdings ist der Abstand der Achsenbeschriftung von der jeweiligen Achse nun größer geworden.

In [32]: unit.set(uscale=2, vscale=1, wscale=1, xscale=1)
   ...: testfigure()

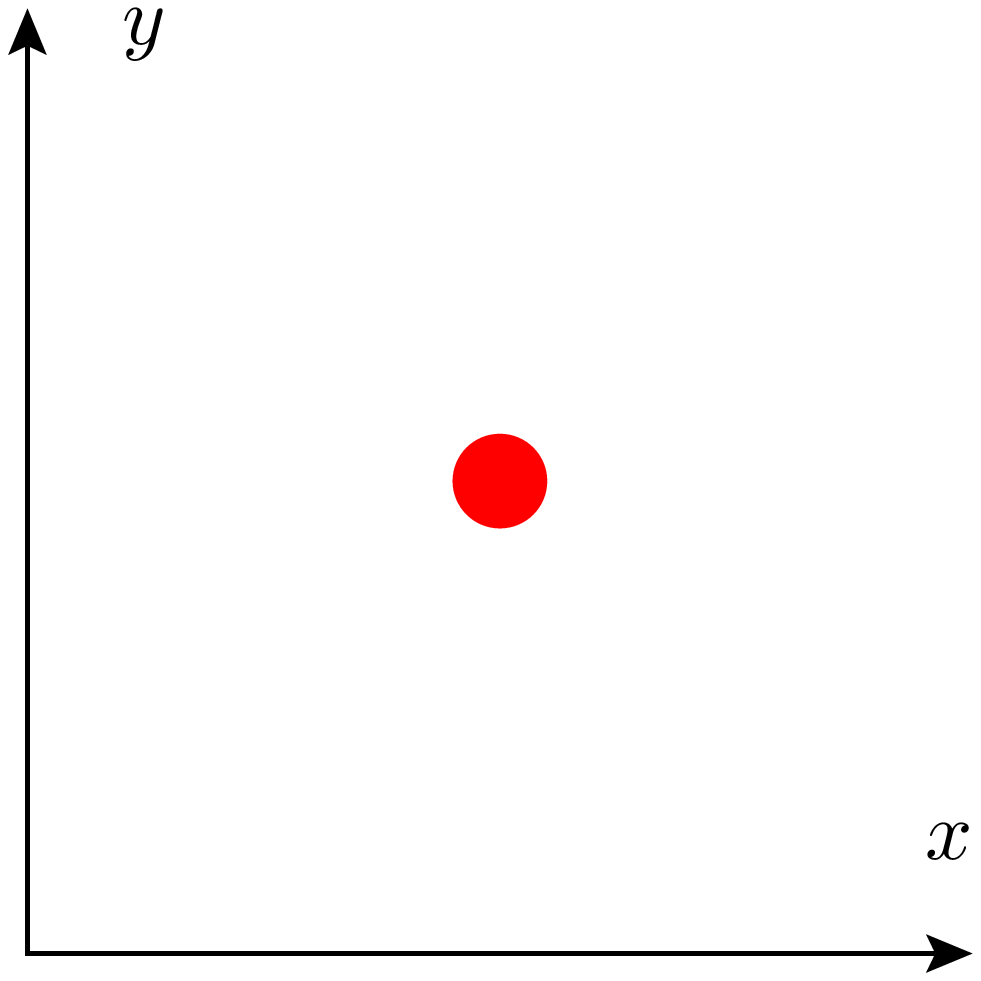
Im nächsten Beispiel wird uscale auf seinen ursprünglichen Wert zurückgesetzt und dafür vscale verdoppelt. Dadurch werden visuelle Elemente doppelt so groß dargestellt. In unserem Fall betrifft dies die Pfeile. Es würden aber zum Beispiel auch Symbole in einer Grafik oder Achsenticks vergrößert dargestellt werden.

In [33]: unit.set(uscale=1, vscale=2, wscale=1, xscale=1)
   ...: testfigure()

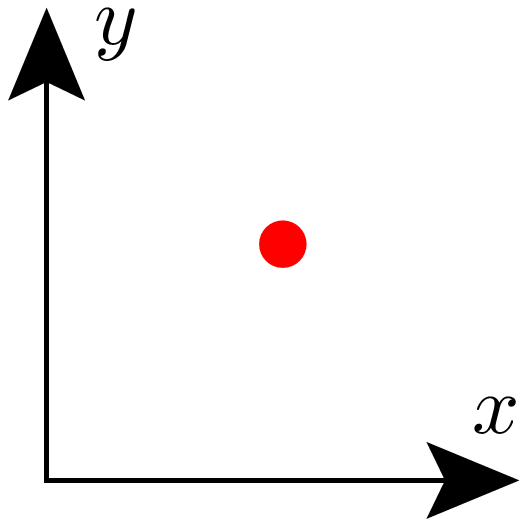
Der Parameter wscale beeinflusst alle Linienbreiten. Möchte man gleichzeitig auch die Pfeilgröße heraufsetzen, so könnte man zusätzlich noch vscale verändern.

In [34]: unit.set(uscale=1, vscale=1, wscale=2, xscale=1)
   ...: testfigure()

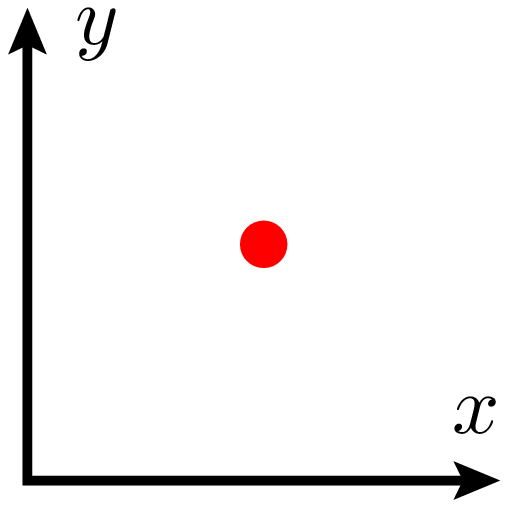
Als letztes verdoppeln wir den Wert von xscale und erreichen auf diese Weise, dass der gesamte Text in doppelter Größe ausgegeben wird. Damit spart man sich unter Umständen, Größenangaben in vielen text-Aufrufen zu ändern. Zudem sind die besprochenen Skalen nützlich, um über mehrere Abbildungen hinweg konsistente Längen zu verwenden.

In [35]: unit.set(uscale=1, vscale=1, wscale=1, xscale=2)
   ...: testfigure()

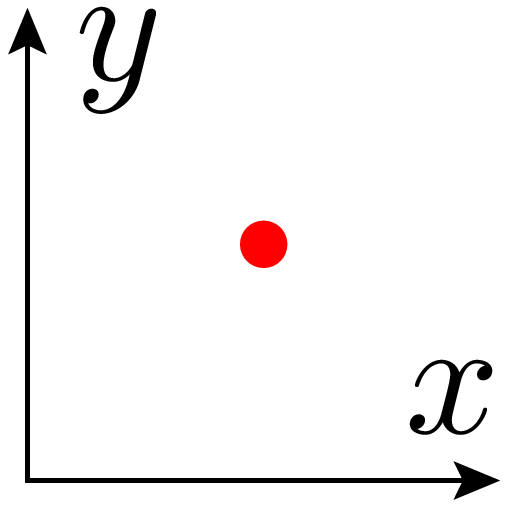
Für die folgenden Beispiele stellen wir alle Skalen wieder auf ihren Standardwert zurück.

In [36]: unit.set(xscale=1)

PyX stellt so genannte Deformer zur Verfügung, die es erlauben, Pfade zu deformieren. Dies kann in bestimmten Fällen sehr nützlich sein. Mit Hilfe eines Deformers ist es zum Beispiel sehr leicht möglich, Kanten mit einem vorgegebenen Radius abzurunden. Zu diesem Zweck fügen wir in der Attributliste im folgenden Beispiel einen Aufruf der smoothed-Methode hinzu.

In [37]: box = path.rect(0, 0, 3, 2)
   ...: c = canvas.canvas()
   ...: c.stroke(box)
   ...: c.stroke(box, [deformer.smoothed(radius=0.5), trafo.translate(3.5, 0)])
   ...: c.stroke(box, [deformer.smoothed(radius=1), trafo.translate(7, 0)])

Besonders elegant ist die Erzeugung der Darstellung einer Feder aus einem Liniensegment durch die Verwendung des cycloid-Deformers, die im folgenden Beispiel dargestellt ist. Um einen optisch ansprechenden Eindruck zu erzielen, stellt man abhängig von der zur Verfügung stehenden Länge den Radius der Zykloide sowie die Zahl der halben Schleifen geeignet ein. Außerdem kann man mit skipfirst und skiplast dafür sorgen, dass ein Teil der Linie am Anfang und am Ende unverändert bleibt. Um den Übergang zwischen dem deformierten Teil und dem unveränderten Teil etwas zu glätten, kann wiederum der smoothed-Deformer zum Einstatz kommen.

In [38]: c = canvas.canvas()
   ...: c.stroke(path.line(0, 0, 5, 0), [deformer.cycloid(radius=0.3,
   ...:                                      halfloops=21,
   ...:                                      skipfirst=0.3*unit.t_cm,
   ...:                                      skiplast=0.6*unit.t_cm),
   ...:                                  deformer.smoothed(radius=0.2)])

Eine Anwendung eines Deformers, bei der der ursprüngliche Pfad mit Hilfe einer »bounding box« erzeugt wird, zeigt das nächste Beispiel. Zunächst wird ein Text definiert, der erst später in einen Canvas eingefügt wird. Daher wird in der ersten Zeile statt c.text die Methode text.text verwendet. Dies erlaubt es uns, die »bounding box« dieses Textes zu bestimmen, anschließend mit enlarged zu vergrößern und uns mit path den zugehörigen Pfad zu beschaffen. Die Vergrößerung der »bounding box« wird hier mit 0.3*unit.t_cm zu 0,3cm spezifiziert. In den Canvas wird dann zunächst der Pfad der vergrößerten »bounding box« in abgerundeter Form und mit roter Farbe gefüllt eingefügt. Anschließend kann dann der weiße Text zum Canvas hinzugefügt werden.

In [39]: mytext = text.text(0, 0, r'\textbf{\sffamily Hallo}', [color.grey(1)])
   ...: textbox = mytext.bbox().enlarged(0.3*unit.t_cm).path()
   ...: c = canvas.canvas()
   ...: c.stroke(textbox, [deco.filled([color.rgb.red]),
   ...:                    deformer.smoothed(radius=0.5)])
   ...: c.insert(mytext)

In vielen Fällen wird man die erzeugte Grafik auch in einer Datei speichern wollen. Dies kann in PyX genauso wie in matplotlib entweder in einem Vektorgrafik- oder einem Bitmapformat erfolgen. Für ersteres stehen aktuell die Ausgaben im PDF-Format sowie in Postscript und Encapsulated Postscript zur Verfügung. Daneben gibt es eine ganze Reihe von Bitmapformaten. Welche Formate verfügbar sind, hängt von den Fähigkeiten des installierten ghostscript-Interpreters ab. Das folgende Beispiel zeigt das Abspeichern eines Canvas im PDF-, im EPS- und im PNG-Format. Verzichtet man in den ersten beiden Fällen auf die Angabe des Dateinamens, so wird der Name des erzeugenden Python-Skripts herangezogen, wobei die Endung py je nach Ausgabeformat durch pdf, ps oder eps ersetzt wird. Häufig ist dies ein sinnvolles Vorgehen, da man beim Kopieren von Skripten auf diese Weise vermeidet, bereits erzeugte Bilder des ursprünglichen Skripts zu überschreiben, wenn man vergisst, den Dateinamen anzupassen. Bei den Bitmapformaten wird das zu erzeugende Format aus der Endung des Dateinamens entnommen, sofern ein Name angegeben wurde. Andernfalls muss das Ausgabegerät spezifiziert werden. Unser Beispiel zeigt außerdem, wie die Auflösung der Bitmapgrafik beeinflusst werden kann.

In [40]: c.writePDFfile('hallo.pdf')
   ...: c.writeEPSfile('hallo.eps')
   ...: c.writeGSfile('hallo.png', resolution=300)

Weitere Informationen über mögliche Optionen beim Abspeichern von Grafiken kann man der Dokumentation entnehmen. Es sei hier nur erwähnt, dass man zum Beispiel beim PDF- und beim Postscript-Format die Papiergröße festlegen oder auch mehrseitige Dokumente erzeugen kann.

Bis jetzt haben wir nur Fähigkeiten von PyX besprochen, die von matplotlib nicht zur Verfügung gestellt werden. Mit PyX kann man jedoch auch genauso gut grafische Darstellungen von Daten erzeugen. Dies soll im Folgenden demonstriert werden.

Genauso wie bisher auch benötigt man für Graphen einen Canvas, allerdings mit erweiterten Fähigkeiten. Für eine gewöhnliche zweidimensionale Darstellung erzeugt man einen Canvas mit Hilfe von graph.graphxy. Wie wir noch sehen werden, lässt sich das Aussehen des Graphen durch geeignete Argumente sehr genau beeinflussen. In dem folgenden, sehr einfachen Beispiel legen wir lediglich die Breite des Graphen fest. Seine Höhe wird dann, da nichts anderes angegeben ist, mit Hilfe des goldenen Schnitts bestimmt. In unserem Beispiel wollen wir eine Reihe von Punkten darstellen, deren Lage durch eine Liste von Tupeln festgelegt wird.

Um der plot-Methode unseres Graphencanvas g die Datenquelle mitzuteilen, verwendet man in diesem Fall die graph.data.points-Methode, die als erstes Argument die Datenliste erhält. Die Argumente x und y geben die Spalte an. Die x-Werte sollen hier die ersten Werte der Tupel sein, die y-Werte die jeweils zweiten Werte. Man könnte aber auch die zweite Spalte gegen die erste Spalte darstellen oder aus längeren Tupeln die gewünschten Spalten nach Bedarf auswählen. Standardmäßig erfolgt nun eine Darstellung der Datenpunkte mit Hilfe von Kreuzen, die nicht durch eine Linie verbunden sind.

In [41]: g = graph.graphxy(width=8)
   ...: data = [(0, 0), (1, 0.5), (2, 3), (3, 4), (4, -0.7)]
   ...: g.plot(graph.data.points(data, x=1, y=2))

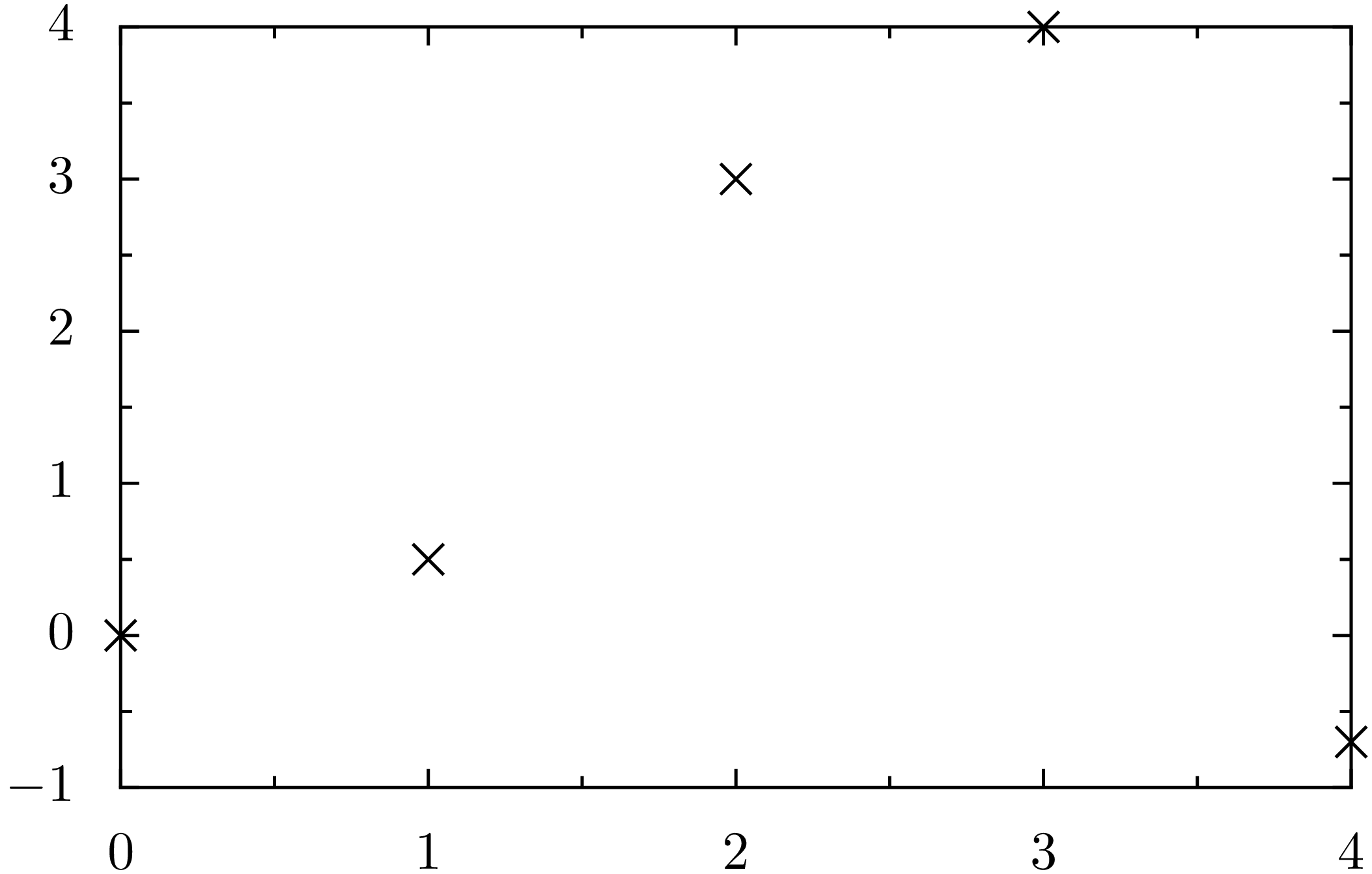
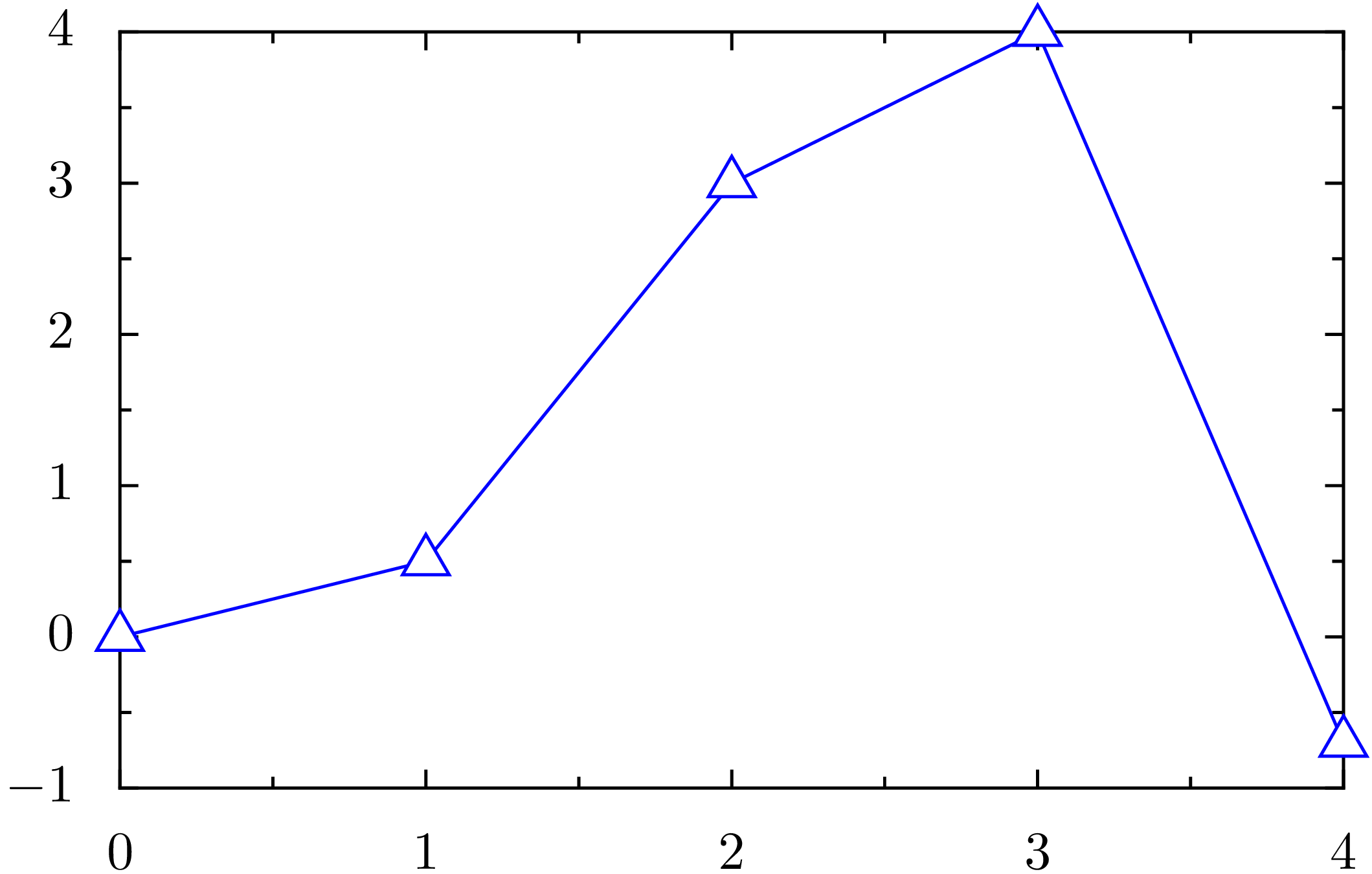
Im nächsten Beispiel wollen wir die Darstellung verbessern, indem wir die Datenpunkte durch blaue gerade Linien verbinden und als Symbole blau umrandete Dreiecke verwenden, die nicht von den Linien durchschnitten werden. Um dies zu realisieren, übergibt man der plot-Methode eine Liste von entsprechenden Attributen, so wie wir es von der stroke- oder der fill-Methode des Canvas her kennen.

Um die Übersichtlichkeit des Codes zu verbessern, haben wir im folgenden Beispiel zwei Variablen definiert, die die Eigenschaften der Linie und der Symbole enthalten. Diese Information könnte man alternativ direkt in der plot-Methode in der letzten Zeile unterbringen. Stattdessen eine Variable zu verwenden, hat neben der Übersichtlichkeit auch den Vorteil, dass sich die Vorgaben in verschiedenen plot-Aufrufen verwenden lassen und so für eine einheitliche Darstellung sorgen sowie das Programmieren nach dem DRY-Prinzip [7] unterstützen.

Mit graph.style.line werden die Eigenschaften der zu zeichnenden Linien festgelegt. Diese werden im Argument als Liste angegeben, selbst wenn es sich, wie im folgenden Beispiel, nur um ein Attribut handelt, das hier die Farbe festlegt. Man könnte beispielsweise auch eine gestrichelte oder gepunktete Linie verlangen. Das Symbol wird mit Hilfe von graph.style.symbol festgelegt, wobei das Argument symbol die Form des Symbols, hier ein Dreieck, angibt. Zudem kann man mit symbolattrs eine Liste von Attributen übergeben, die das Aussehen des Symbols genauer festlegen. In unserem Fall wird verlangt, dass der Rand des Symbols blau ist und das Innere weiß gefüllt wird. Mit letzterem wird sichergestellt, dass die Linien die Symbole nicht schneiden.

In [42]: g = graph.graphxy(width=8)
   ...: data = [(0, 0), (1, 0.5), (2, 3), (3, 4), (4, -0.7)]
   ...: myline = graph.style.line([color.rgb.blue])
   ...: mysymbol = graph.style.symbol(symbol=graph.style.symbol.triangle,
   ...:                               symbolattrs=[deco.filled([color.grey(1)]),
   ...:                                            deco.stroked([color.rgb.blue])])
   ...: g.plot(graph.data.points(data, x=1, y=2), [myline, mysymbol])

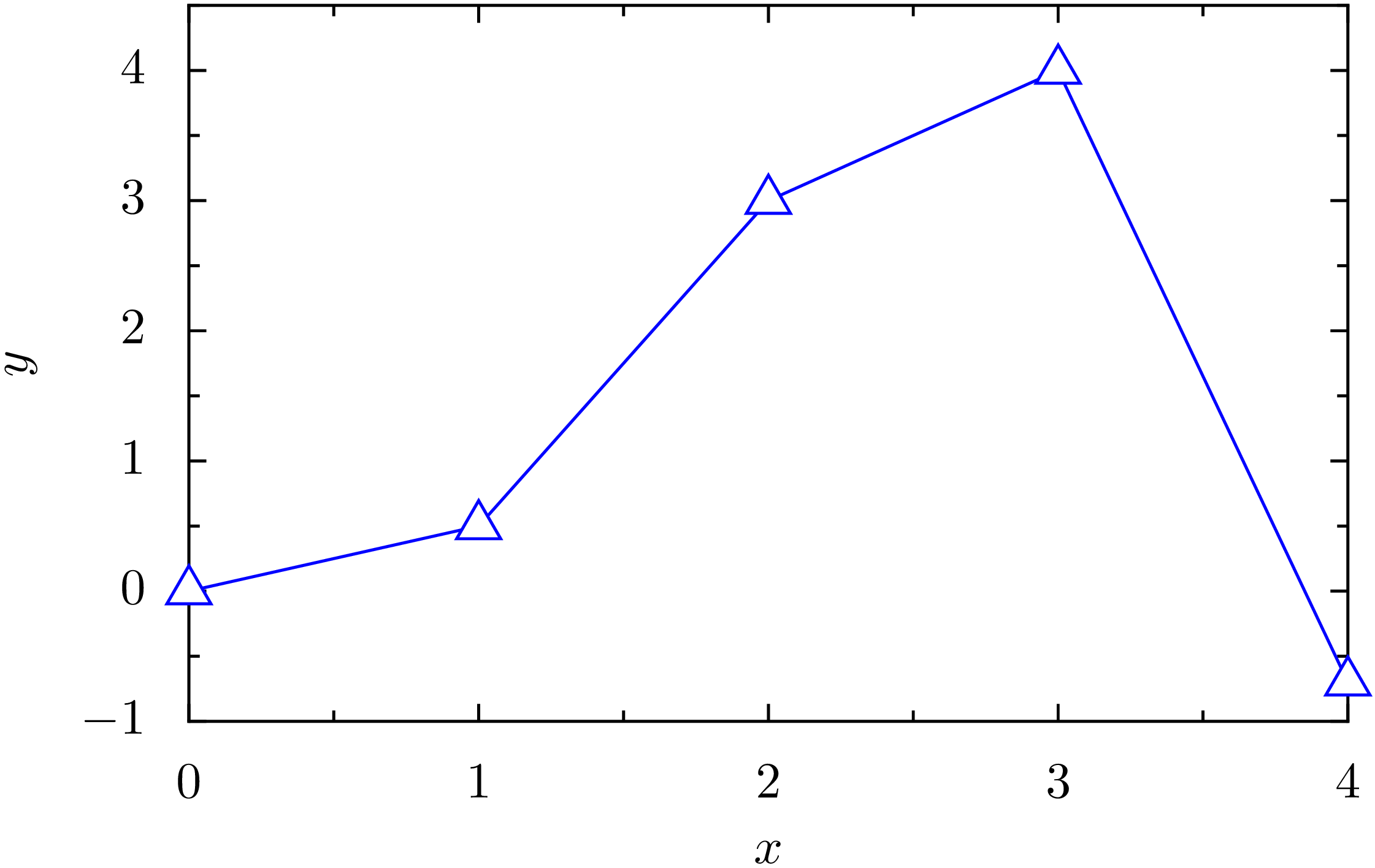
Im nächsten Beispiel nehmen wir Veränderungen an den Achsen vor. Hierzu definiert man im Graphencanvas mit Hilfe der Argumente x und y die Eigenschaften der zugehörigen Achsen. Mit graph.axis.lin erhält man eine linear eingeteilte Achse, deren Eigenschaften mit den zugehörigen Argumenten übergeben werden können. Dies ist zum Beispiel der Achsenumfang, der mit min und/oder max festgelegt werden kann, oder der Achsentitel, der mit title übergeben wird, wobei wie beim Text TeX- oder LaTeX-Syntax verwendet werden kann. In dem folgenden Beispiel wird unter anderem der Wertebereich der y-Achse vergrößert, damit das Symbol bei \(x=3\) im Innern des y-Wertebereichs liegt.

In [43]: g = graph.graphxy(width=8,
   ...:                   x=graph.axis.lin(title='$x$'),
   ...:                   y=graph.axis.lin(min=-1, max=4.5, title='$y$'))
   ...: data = [(0, 0), (1, 0.5), (2, 3), (3, 4), (4, -0.7)]
   ...: myline = graph.style.line([color.rgb.blue])
   ...: mysymbol = graph.style.symbol(symbol=graph.style.symbol.triangle,
   ...:                               symbolattrs=[deco.filled([color.grey(1)]),
   ...:                                            deco.stroked([color.rgb.blue])])
   ...: g.plot(graph.data.points(data, x=1, y=2), [myline, mysymbol])

Bis jetzt haben wir als Datenquelle eine Liste von Tupeln verwendet. PyX kann alternativ auch Daten aus einer Datei einlesen oder aus vorgegebenen Funktionen berechnen. Dabei sind auch parametrisch definierte Funktionen möglich.

Wir wollen nun eine Darstellung von verschiedenen Potenzfunktionen erzeugen. Um eine Funktion darzustellen, wählt man die graph.data.function-Methode, in der man den funktionalen Zusammenhang zwischen x und y in einer Zeichenkette angibt. Normalerweise wählt PyX selbst die Zahl der Punkte, an denen die Funktion ausgewertet wird. Da wir die zugehörigen Punkte mit Symbolen darstellen wollen, legen wir jedoch die Zahl der Punkte mit Hilfe des Arguments points fest.

In unserem Beispiel werden mittels eines einzigen Aufrufs der plot-Methode mehrere Funktionen gezeichnet. Hierzu wird eine ganze Liste von function-Aufrufen als erstes Argument übergeben. Dabei ist es in PyX sehr elegant möglich festzulegen, wie die einzelnen Funktionsgraphen dargestellt werden sollen. Wie schon im vorigen Beispiel benutzen wir graph.style.line, um die Attribute der Linien festzulegen. Die entsprechende Liste enthält zwei Aufrufe von attr.changelist, die festlegen, wie sich bestimmte Attribute beim Wechsel von einer Linie zur nächsten ändern. Der erste Aufruf geht die in der vierten Zeile definierte Farbliste der Reihe nach durch. Der zweite Aufruf enthält eine Liste, die nur aus einem Element besteht und in diesem Fall dazu führt, dass alle Linien durchgezogen sind.

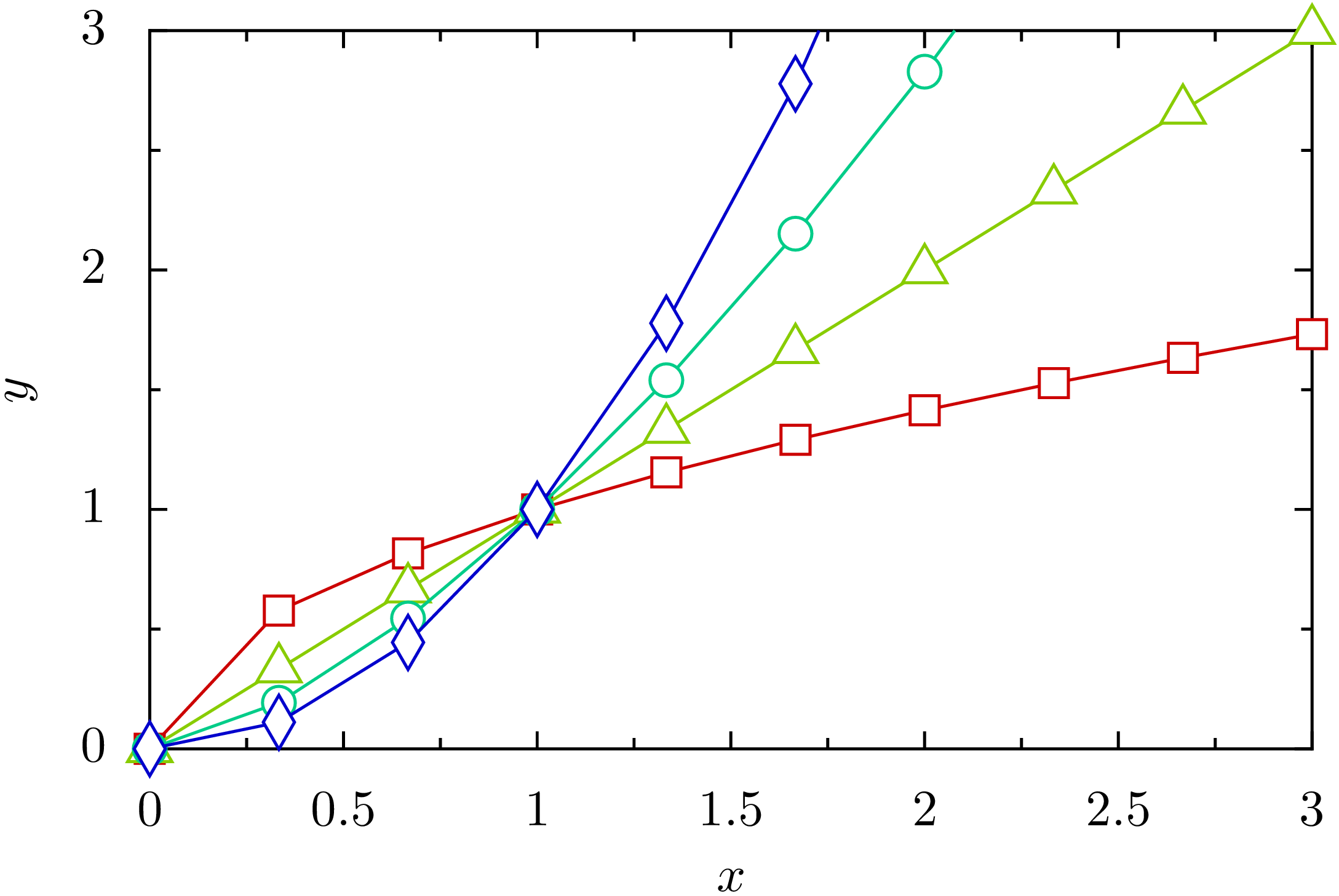
Bei der Symbolart verwenden wir eine vordefinierte Symbolliste, die der Reihe nach Quadrat, Dreieck, Kreis, Raute, Kreuz und Pluszeichen verwendet. In unserem Beispiel mit nur vier Funktionen kommen nur die ersten vier Symbole zum Einsatz. Damit die Farbe der Symbole zur Farbe der Linien passt, übergeben wir unsere Farbliste auch an die Liste der Symbolattribute. Zudem legen wir, wie schon im vorigen Beispiel, fest, dass die Symbole weiß zu füllen sind. Damit ergibt sich ingesamt das unter dem Code dargestellte Bild.

In [44]: g = graph.graphxy(width=8,
   ...:                   x=graph.axis.lin(min=0, max=3, title='$x$'),
   ...:                   y=graph.axis.lin(min=0, max=3, title='$y$'))
   ...: colors = [color.hsb(2*n/9, 1, 0.8) for n in range(0, 4)]
   ...: mylines = graph.style.line(lineattrs=[
             attr.changelist(colors), attr.changelist([style.linestyle.solid])
                                             ])
   ...: mysymbols = graph.style.symbol(symbol=graph.style.symbol.changesquare,
   ...:                                symbolattrs=[
                 attr.changelist(colors), deco.filled([color.grey(1)])
                                                   ])
   ...: g.plot([graph.data.function('y(x)=x**{}'.format(exponent/2), points=10)
   ...:                                         for exponent in range(1, 5)],
   ...:        [mylines, mysymbols])

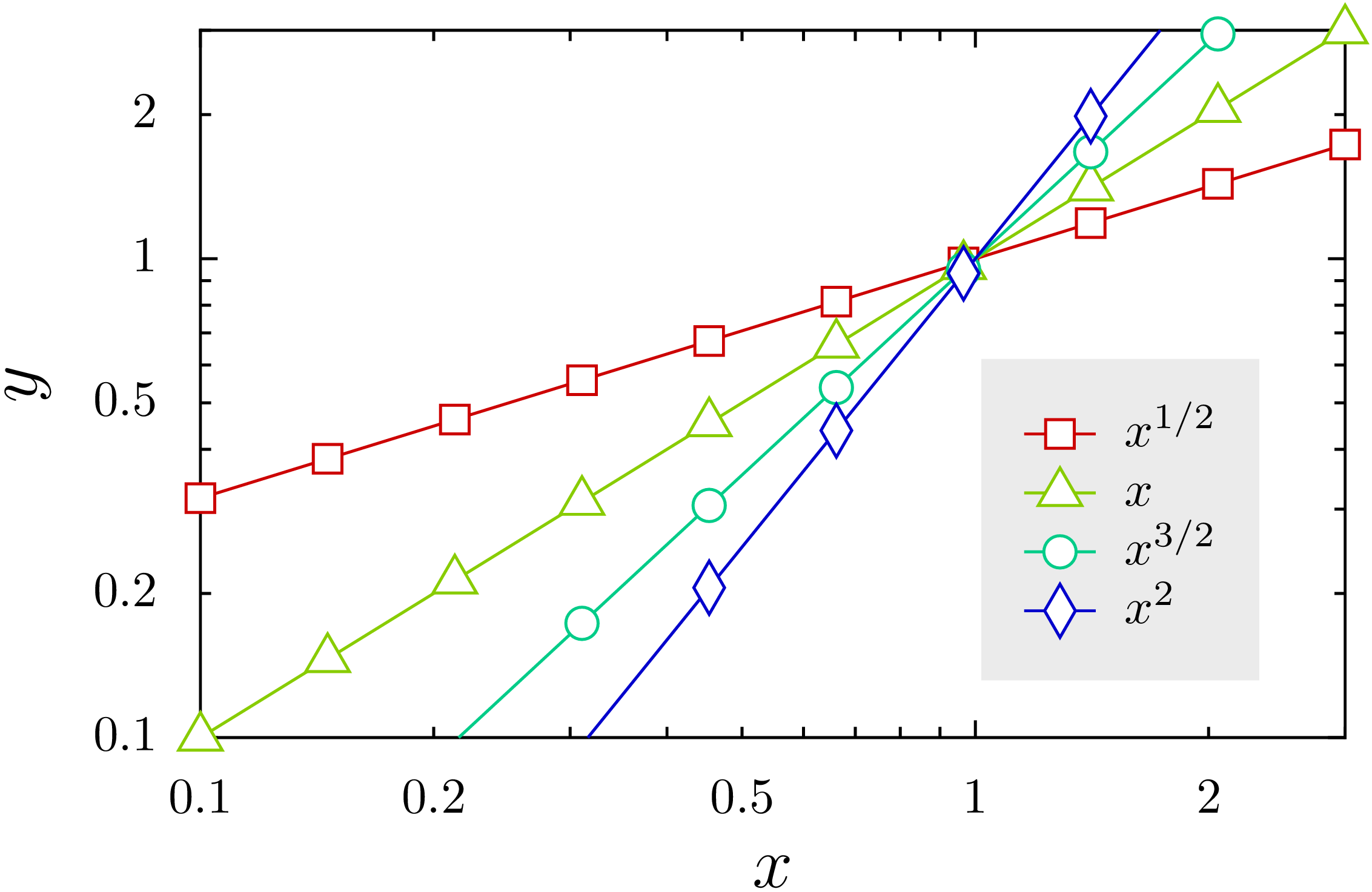
Im nächsten Schritt stellen wir die Abbildung des vorigen Beispiels auf eine doppelt-logarithmische Darstellung um und fügen zusätzlich eine Legende hinzu. Logarithmische Achsen erhält man einfach dadurch, dass man im Graphencanvas die x-Achse und/oder y-Achse mit Hilfe eines Aufrufs der graph.axis.log-Methode definiert. Beim Achsenumfang ist darauf achten, dass dieser eine logarithmische Darstellung erlauben muss. Negative Werte einschließlich der Null müssen also ausgeschlossen sein.

Um eine Legende zu erzeugen, definiert man das key-Argument des Graphencanvas entsprechend. Im Beispiel führt der Aufruf der graph.key.key-Methode dazu, dass die Legende unten rechts (br = »bottom right«) positioniert wird und die Angabe des Wertes für das Argument dist den Abstand zwischen den einzelnen Legendeneinträgen gegenüber dem Standardwert verringert, die Legende also etwas komprimierter darstellt wird. Schließlich verlangen wir mit Hilfe der an keyattrs übergebenen Liste, dass die Legende grau hinterlegt wird.

Der in der Legende dargestellte Text ist für jeden Datensatz im title-Argument zu übergeben. Im Beispiel haben wir hierfür eine Funktion definiert, die je nach ganz- oder halbzahligem Argument die Darstellung unter Verwendung der TeX-Syntax geeignet wählt.

In [45]: def keytitle(dblexponent):
   ...:     if dblexponent == 2: return '$x$'
   ...:     if dblexponent % 2:
   ...:         return '$x^{{{}/2}}$'.format(dblexponent)
   ...:     else:
   ...:         return '$x^{}$'.format(dblexponent//2)
   ...:
   ...: g = graph.graphxy(width=8,
   ...:                   x=graph.axis.log(min=0.1, max=3, title='\Large $x$'),
   ...:                   y=graph.axis.log(min=0.1, max=3, title='\Large $y$'),
   ...:                   key=graph.key.key(pos="br", dist=0.1,
   ...:                             keyattrs=[deco.filled([color.grey(0.9)])]))
   ...: g.plot([graph.data.function('y(x)=x**{}'.format(exponent/2),
   ...:                             points=10, title=keytitle(exponent))
   ...:                                       for exponent in range(1, 5)],
   ...:        [mylines, mysymbols])

Gelegentlich möchte man die Ablesung von Werten in einem Graphen durch Gitterlinien unterstützen. Dies lässt sich unabhängig voneinander für beide Achsen mit Hilfe des painter-Arguments festlegen. Dazu geben wir dem Painter graph.axis.painter.regular, der schon bisher für die Darstellung der Achsen zuständig war, ein Attributargument mit. Wie sonst auch muss es sich dabei um eine Liste handeln, die in unserem Fall nur vorgibt, dass die Gitterlinien gepunktet sein sollen. Außerdem modifizieren wir unser Beispiel noch dahingehend, dass der Hintergrund der Legende nun weiß gehalten ist. Dafür wird der Rahmen mit einer schwarzen Linie gezeichnet. Diese Änderungen erhält man durch eine entsprechende Anpassung der Liste des keyattrs-Arguments.

In [46]: mygridattrs = [style.linestyle.dotted]
   ...: mypainter = graph.axis.painter.regular(gridattrs=mygridattrs)
   ...: g = graph.graphxy(width=8,
   ...:                   x=graph.axis.log(min=0.1, max=3, title='\Large $x$',
   ...:                                    painter=mypainter),
   ...:                   y=graph.axis.log(min=0.1, max=3, title='\Large $y$',
   ...:                                    painter=mypainter),
   ...:                   key=graph.key.key(pos="br", dist=0.1,
   ...:                                     keyattrs=[deco.filled([color.grey(1)]),
   ...:                                               deco.stroked()]))
   ...: g.plot([graph.data.function('y(x)=x**{}'.format(exponent/2),
   ...:                             points=10, title=keytitle(exponent))
   ...:                                               for exponent in range(1, 5)],
   ...:        [mylines, mysymbols])

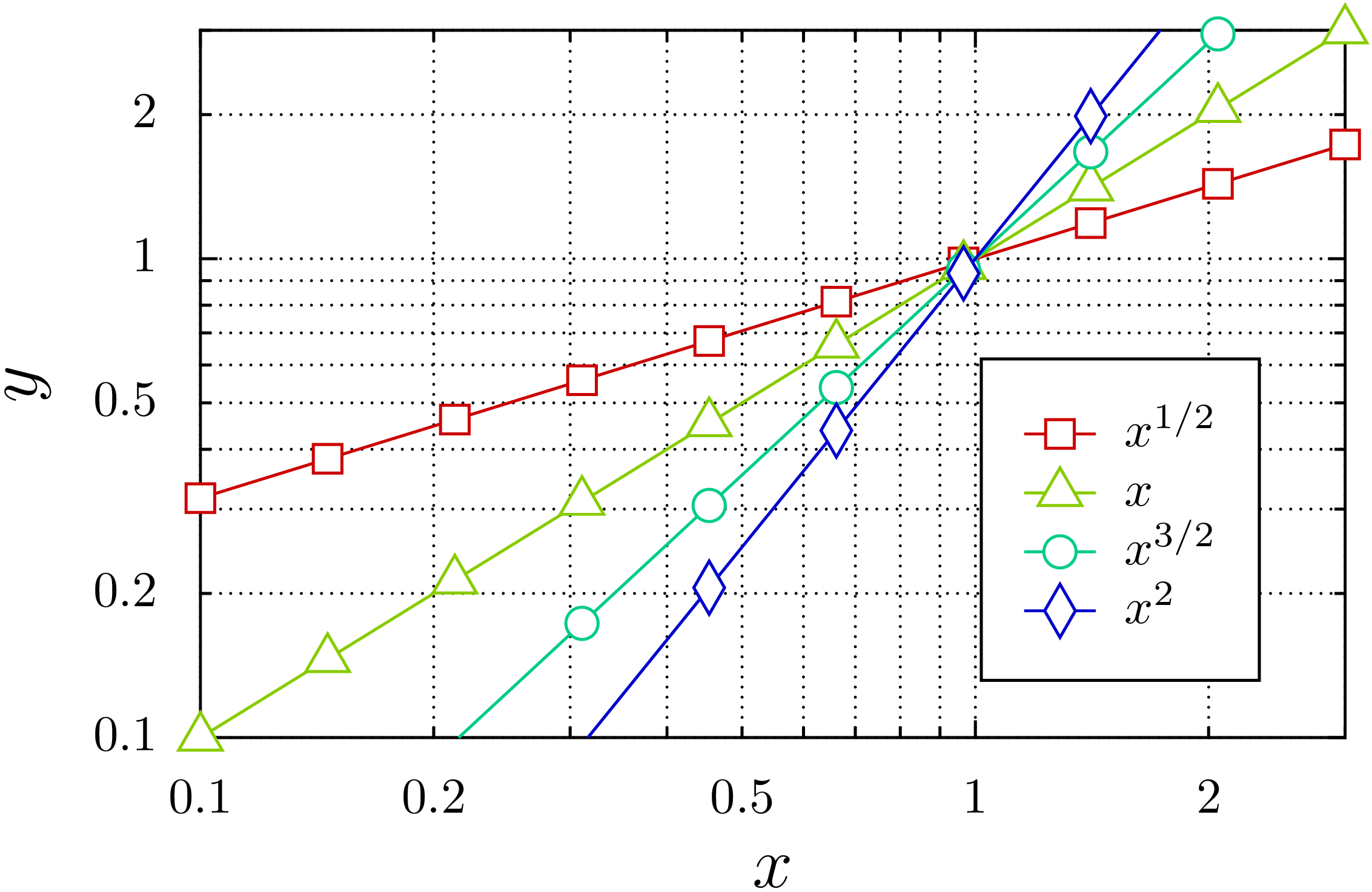
In matplotlib hatten wir gesehen, dass die Achseneinteilung recht flexibel gestaltet werden kann. Dies ist auch in PyX möglich. Wir hatten schon im Zusammenhang mit der Erzeugung von Gitterlinien gesehen, wie sich Achseneigenschaften beeinflussen lassen. Bei der y-Achse modifizieren wir wieder die Darstellung der Achse, genauer der zugehörigen Ticks, mit Hilfe der graph.axis.painter.regular-Methode. Um die Ticks nach außen zeigen zu lassen, setzen wir die innerticklength auf None während die outerticklength auf den Standardwert gesetzt wird, den bisher innerticklength hatte.

Ein weiterer Aspekt, den wir an der y-Achse gegenüber dem Standardverhalten verändern wollen, ist der Abstand zwischen den Ticks. Für die Einteilung der Achsen ist der »parter« zuständig. Wir geben dem bereits bisher im Verborgenen für uns tätigen graph.axis.parter.linear über das Argument tickdists eine Liste mit, die den Abstand zwischen Ticks und Subticks enthält. Durch die Wahl der Werte in unserem Beispiele erreichen wir, dass der Abstand zwischen zwei Ticks in fünf Intervalle unterteilt wird.

Schließlich wollen wir noch die Beschriftung der x-Achse modifizieren. Hierfür ist der »texter« zuständig. Wir verwenden hier graph.axis.texter.rational, der die Achsenbeschriftung mit Hilfe von Brüchen darstellt und stellen den Beschriftungen ein π hintenan. Damit die Beschriftung zum tatsächlichen Wert passt, müssen wir im Gegenzug die Werte durch π dividieren, was mit Hilfe des Arguments divisor eingestellt wird.

In [47]: mypainter = graph.axis.painter.regular(
   ...:                     innerticklength=None,
   ...:                     outerticklength=graph.axis.painter.ticklength.normal)
   ...: g = graph.graphxy(width=8,
   ...:                   x=graph.axis.linear(min=0, max=2*pi, divisor=pi,
   ...:                        texter=graph.axis.texter.rational(suffix=r"\pi")),
   ...:                   y=graph.axis.linear(
                               parter=graph.axis.parter.linear(tickdists=[1,0.2]),
   ...:                        painter=mypainter))
   ...: g.plot(graph.data.function('y(x)=sin(x)'))

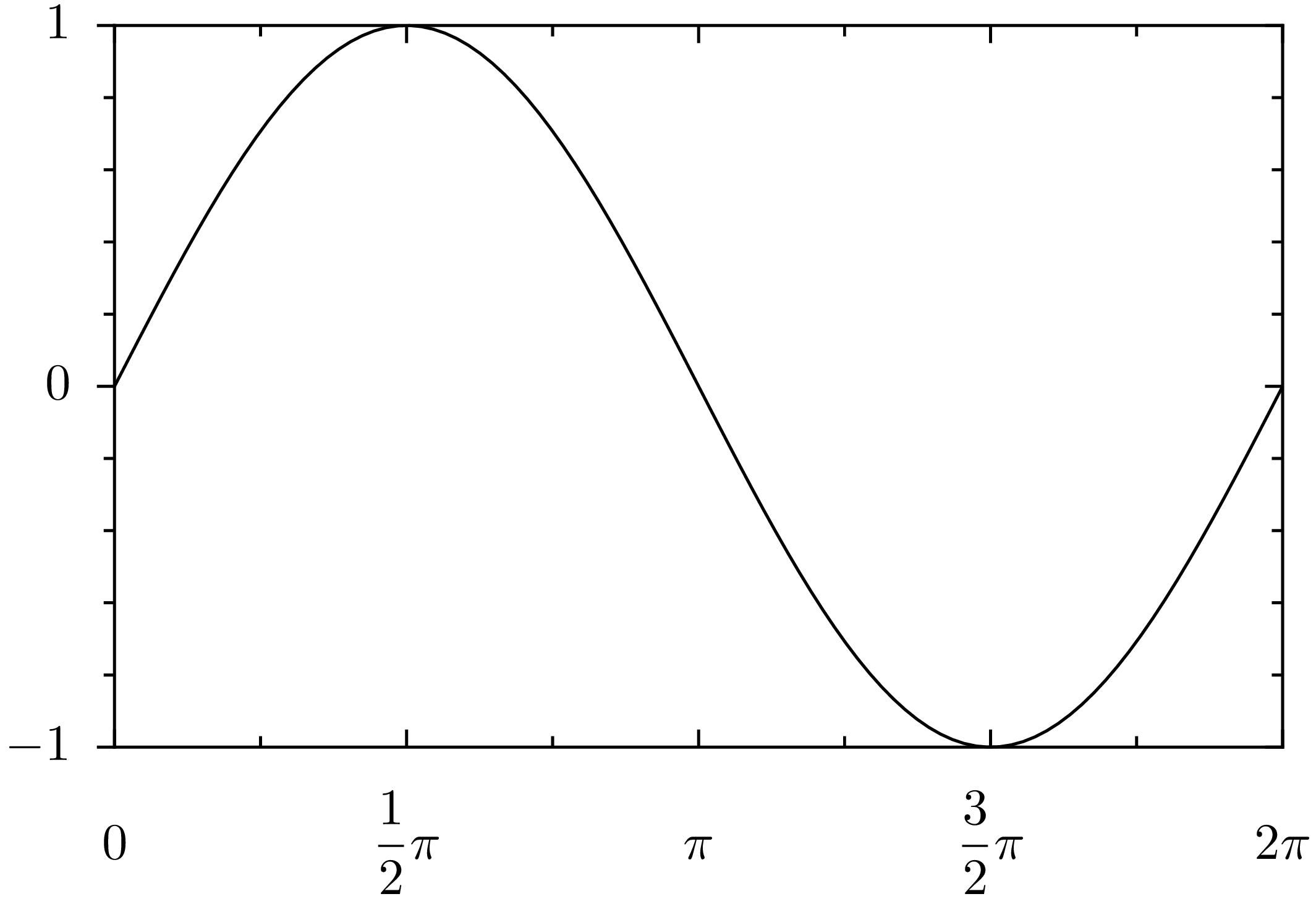
Um eine Funktion zweier Variablen darzustellen, eignen sich neben Konturgrafiken, die wir im Zusammenhang mit matplotlib besprochen haben, auch zweidimensionale Farbdarstellungen. Der größte Teil des folgenden Beispielcodes dient dazu, eine Liste von Daten zu erzeugen, die nun aus Tupeln mit jeweils drei Einträgen besteht. Die ersten beiden Einträge geben den Ort in der Ebene an und der dritte Eintrag entspricht dem Funktionswert an dieser Stelle. Wie in unserem ersten Graphenbeispiel verwenden wir wieder graph.data.points. Für die Darstellung benötigen wir jedoch jetzt nicht mehr nur noch x- und y-Werte, sondern auch einen Farbwert, der sich aus dem Funktionswert ergibt. Das Argument color erhält daher den Wert 3, entsprechend der dritten Datenspalte. Außerdem müssen wir den Zeichenstil auf graph.style.density abändern. Damit wir keine Graustufendarstellung erhalten, geben wir dort noch den Farbgradienten an, der die Abbildungen von den Daten auf zugehörige Farben bewerkstelligt.

In [48]: import numpy as np
   ...: def f(x, y):
   ...:     return cos(x**2+y**2)*sin(2*y**2)
   ...:
   ...: xmin = -2
   ...: xmax = 2
   ...: ymin = -2
   ...: ymax = 2
   ...: npts = 100
   ...: data = [(x, y, f(x, y)) for x in np.linspace(xmin, xmax, npts)
   ...:                         for y in np.linspace(xmin, xmax, npts)]
   ...: g = graph.graphxy(height=8, width=8,
   ...:                   x=graph.axis.linear(title=r'$x$'),
   ...:                   y=graph.axis.linear(title=r'$y$'))
   ...: g.plot(graph.data.points(data, x=1, y=2, color=3, title='$f(x,y)$'),
   ...:        [graph.style.density(gradient=color.rgbgradient.Rainbow)])

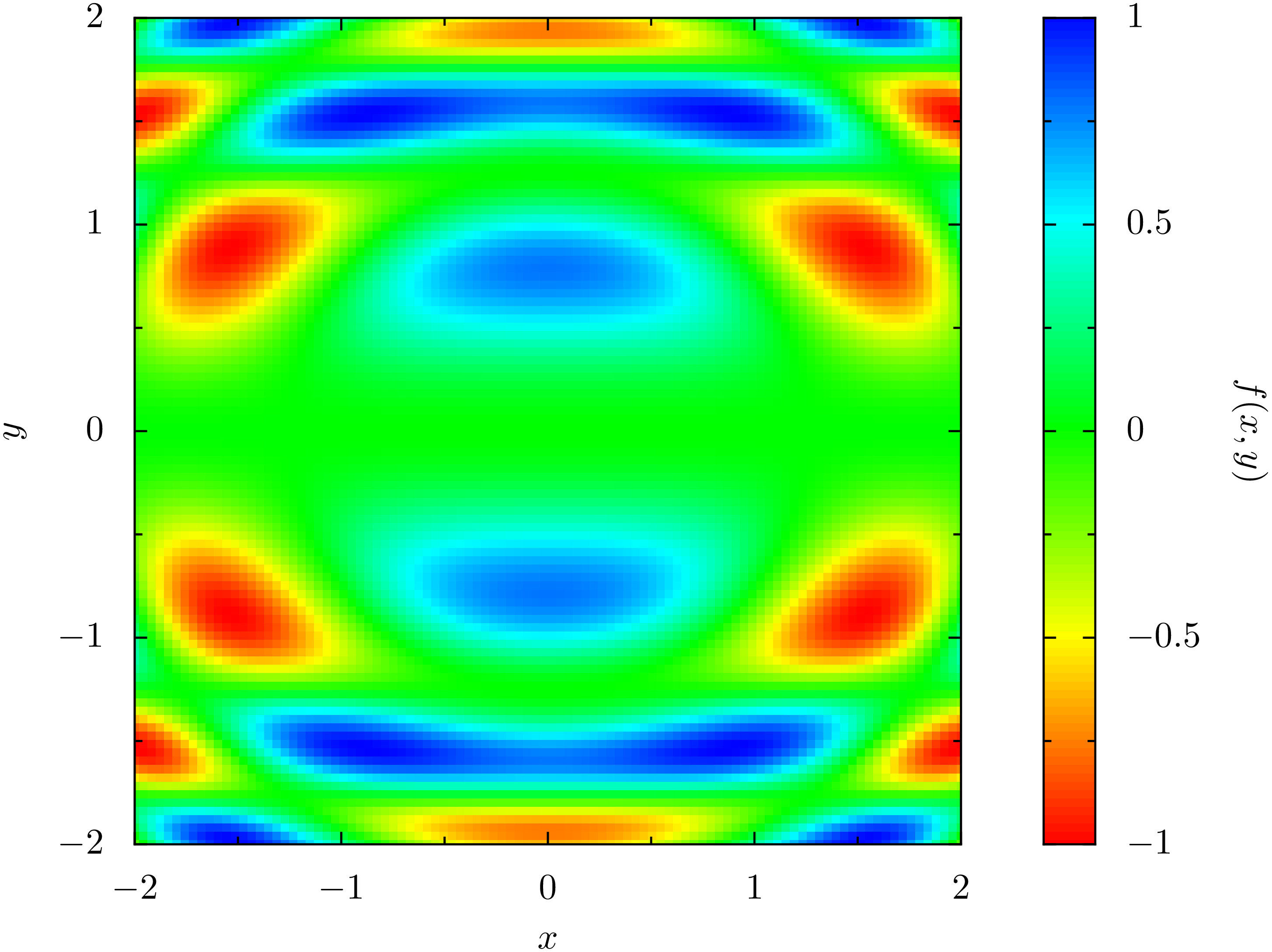
Konturlinien werden derzeit von PyX nicht unterstützt. Man kann sich allerdings bis zu einem gewissen Grad damit behelfen, dass man auf das Paket scikit-image [8] zurückgreift. Dieses Paket bietet eine Vielzahl interessanter Methoden zur Bildbearbeitung mit Python. Das measure-Paket bietet unter anderem die Möglichkeit, in einem zweidimensionalen Datensatz zu einem vorgegebenen Wert die Konturlinie oder gegebenenfalls mehrere Konturlinien zu bestimmen. Dabei ist allerdings zu beachten, dass sich die Funktion find_contours nicht um die in unserem Fall durchaus vorhandenen x- und y-Koordinaten kümmert, sondern mit Pixelpositionen arbeitet, wie es für ein gerastertes Bild adäquat ist. Daher müssen wir unsere in der Liste data gespeicherten Daten zunächst in ein NumPy-Array umbauen, das die richtigen Dimensionen besitzt und lediglich die Funktionswerte enthält. Anhand dieser Daten berechnet find_contours dann eine Liste von Konturdaten. Diese müssen wir vor der Verwendung noch in unsere Problemdaten zurückwandeln, was problemlos gelingt, da wir die Minimal- und Maximalwerte auf der x- und der y-Achse sowie die Zahl der Punkte kennen. Anschließend können wir die Konturen mit einem plot-Aufruf in unserem Farbbild einzeichnen lassen.

In [49]: from skimage.measure import find_contours
   ...:
   ...: data = [(x, y, f(x, y)) for x in np.linspace(xmin, xmax, npts)
   ...:                         for y in np.linspace(ymin, ymax, npts)]
   ...: g = graph.graphxy(height=8, width=8,
   ...:                   x=graph.axis.linear(title=r'$x$'),
   ...:                   y=graph.axis.linear(title=r'$y$'))
   ...: g.plot(graph.data.points(data, x=1, y=2, color=3, title='$f(x,y)$'),
   ...:        [graph.style.density(gradient=color.rgbgradient.Rainbow)])
   ...:
   ...: for level in (-0.5, 0.5):
   ...:     contours = find_contours(np.array([d[2] for d in data]).reshape(
                                                             npts, npts), level)
   ...:     for c in contours:
   ...:         c_rescaled = [(xmin+x*(xmax-xmin)/(npts-1),
   ...:                        ymin+y*(ymax-ymin)/(npts-1)) for x, y in c]
   ...:         g.plot(graph.data.points(c_rescaled, x=1, y=2),
   ...:                                       [graph.style.line()])

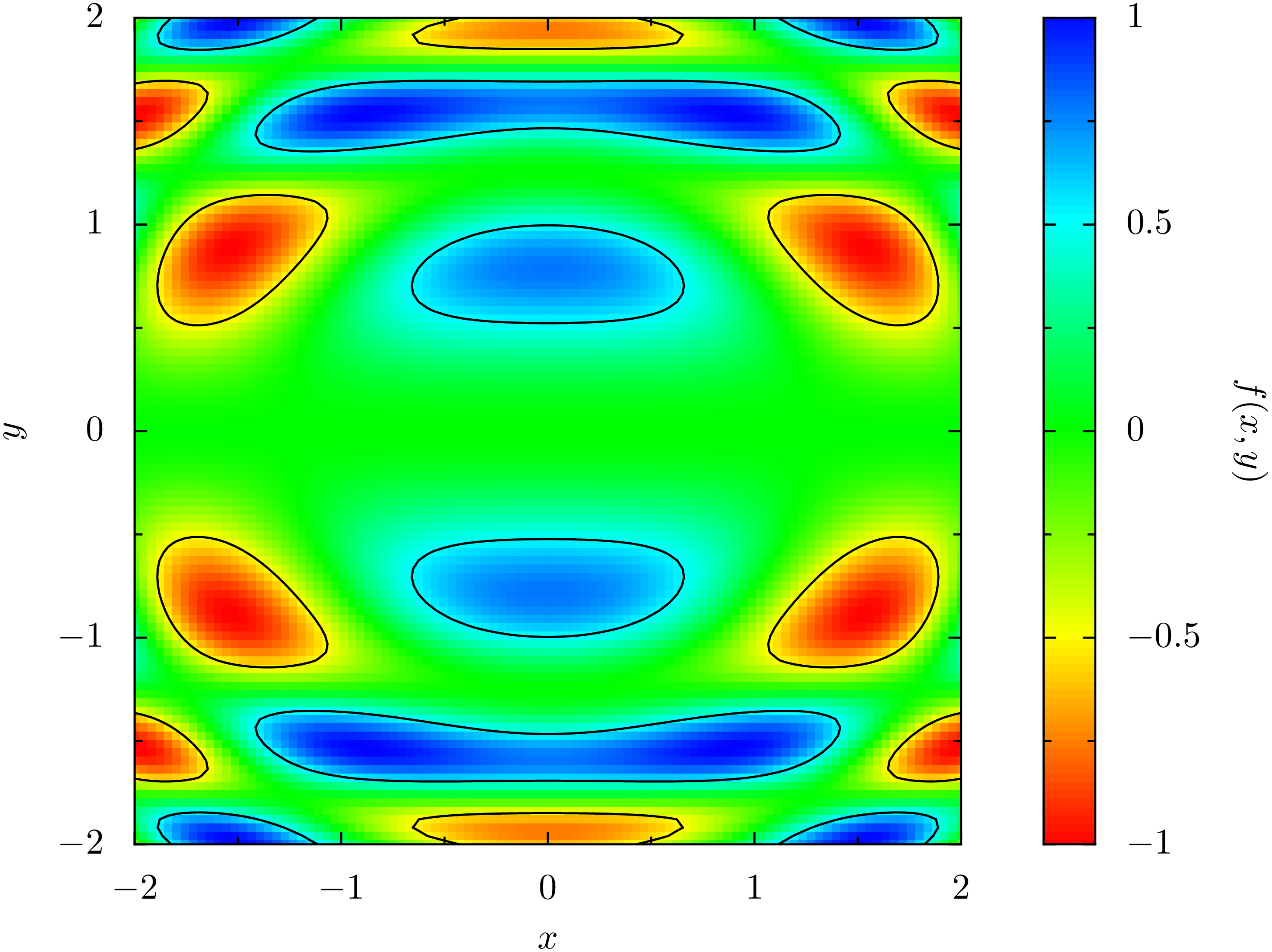
Wenn man zwei Graphen in einer Abbildung zusammenfassen will, so sollen häufig einander entsprechende Achsen gekoppelt werden, also den gleichen Achsenumfang und die gleiche Achseneinteilung besitzen. Häufig soll zudem bei einer Achse die Beschriftung entfallen. Im folgenden Beispiel verwenden wir zwei Graphencanvasse g1 für den unteren Graphen und g2 für den oberen Graphen, die in einen gemeinsamen Canvas c eingefügt werden. Dies kann, wie aus dem nachstehenden Code ersichtlich wird, bereits bei der Instantiierung der beiden Graphen geschehen. Dabei muss man allerdings darauf achten, dass die beiden Graphen relativ zueinander geeignet positioniert werden. Nachdem die untere linke Ecke des unteren Graphen im Ursprung liegt, können wir die vertikale Position ypos des oberen Graphen dadurch festlegen, dass wir die Höhe des unteren Graphen g1.height noch etwas vergrößern, hier um den Wert 0,5.

Da die beiden Graphen nun vertikal angeordnet sind, ist es sinnvoll, die x-Achse des oberen Graphen and die x-Achse des unteren Graphen zu koppeln. Dies geschieht, indem man für die x-Achse des oberen Graphen eine graph.axis.linkedaxis wählt, der man als Argument mit Hilfe von g1.axes["x"] die x-Achse des unteren Graphen übergibt.

Schließlich möchte man häufig die einzelnen Graphen mit einer Bezeichnung versehen, um auf sie Bezug nehmen zu können. Zur Positionierung eignen sich die Attribute xpos und ypos, die die linke untere Ecke eines Graphen angeben, sowie width und height, die die Breite und Höhe des Graphen angeben. In diesem Zusammenhang sei noch darauf hingewiesen, dass wir in diesem Beispiel von der automatischen Bestimmung der Höhe aus der Breite mit Hilfe des goldenen Schnitts abgewichen sind, indem wir die Höhe explizit gesetzt haben.

In [50]: c = canvas.canvas()
   ...: g1 = c.insert(graph.graphxy(width=8, height=3,
   ...:                             x=graph.axis.lin(title='\large $t$'),
   ...:                             y=graph.axis.lin(title='\large $x$')))
   ...: g1.plot(graph.data.function("y(x)=x*exp(-x)", min=0, max=10),
   ...:         [graph.style.line(lineattrs=[color.rgb.blue])])
   ...: g1.text(g1.xpos-1, g1.height, '\Large (b)',
   ...:         [text.halign.right, text.valign.top])
   ...: g2 = c.insert(graph.graphxy(width=8, height=3,
   ...:                             ypos=g1.height+0.5,
   ...:                             x=graph.axis.linkedaxis(g1.axes["x"]),
   ...:                             y=graph.axis.lin(title='x')))
   ...: g2.plot(graph.data.function("y(x)=exp(-0.2*x)*sin(3*x)"),
   ...:                 [graph.style.line(lineattrs=[color.rgb.blue])])
   ...: g2.text(g2.xpos-1, g2.ypos+g2.height, '\Large (a)',
   ...:         [text.halign.right, text.valign.top])

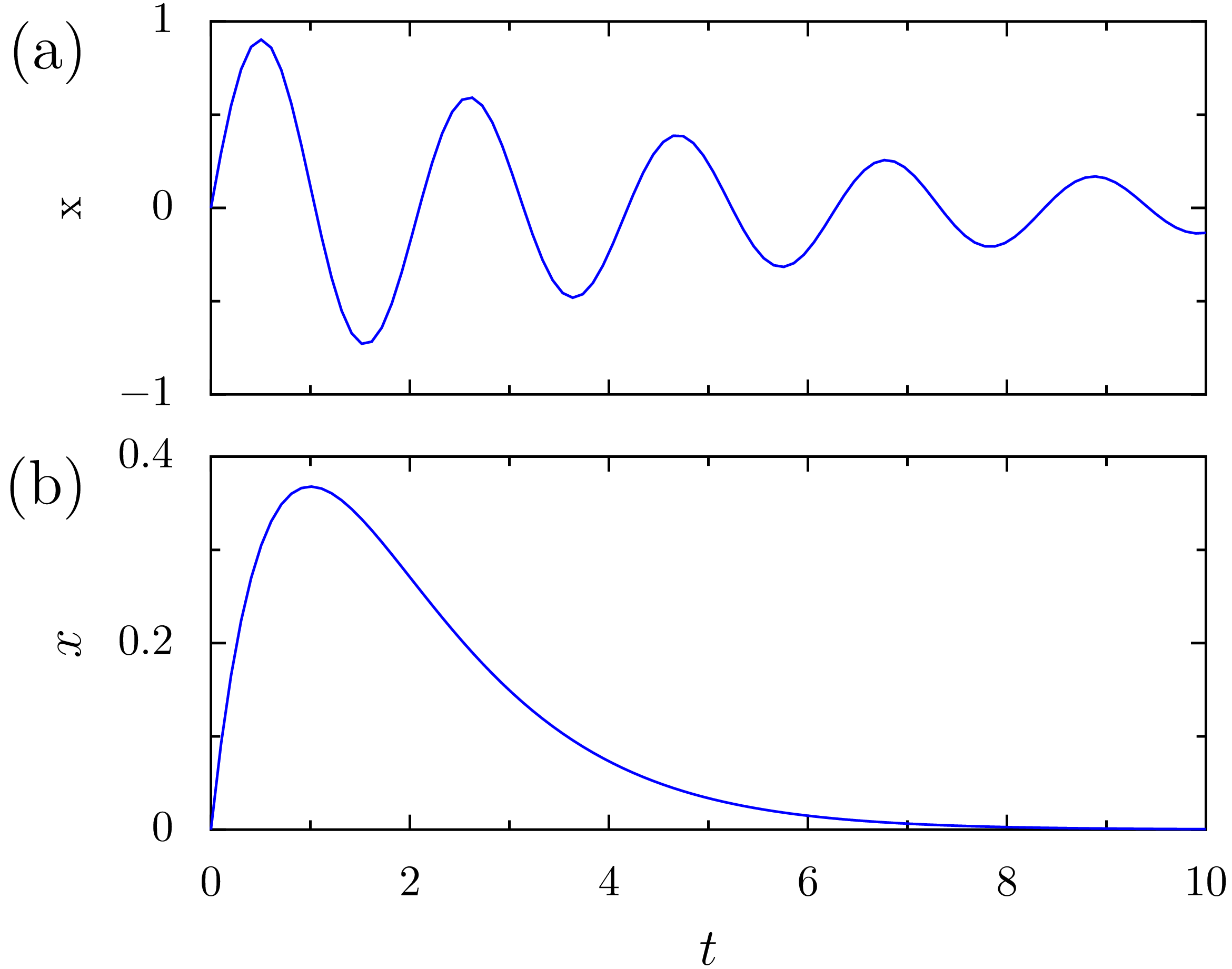
Abschließend wollen wir uns noch dreidimensionalen Darstellungen zuwenden und zu Beginn ein möglichst einfaches Beispiel betrachten. Zunächst werden Daten auf einem zweidimensionalen Gitter erzeugt und in einer Liste, die hier wieder den Namen data besitzt, mit Tupeln zu je drei Einträgen abgelegt. Im Unterschied zu den vorhergehenden Beispielen müssen wir den Canvas des Graphen nicht mit graph.graphxy sondern mit graph.graphxyz erzeugen, da wir ja drei Achsen x, y und z benötigen. Entsprechend müssen wir im Argument von graph.data.points auch die Spalte angeben, aus der die Daten für die z-Achse genommen werden sollen. In unserem Fall ist dies die Spalte 3. Schließlich muss man in der Attributliste der plot-Methode mit graph.style.surface angeben, dass die Daten in Form einer Fläche dargestellt werden sollen. So lange nichts anderes festgelegt wird, wird diese Fläche in Grautönen dargestellt.

In [51]: data = [(x, y, x**2-y**2)
   ...:          for x in np.linspace(-1, 1, 50) for y in np.linspace(-1, 1, 50)]
   ...: g = graph.graphxyz(size=4)
   ...: g.plot(graph.data.points(data, x=1, y=2, z=3), [graph.style.surface()])

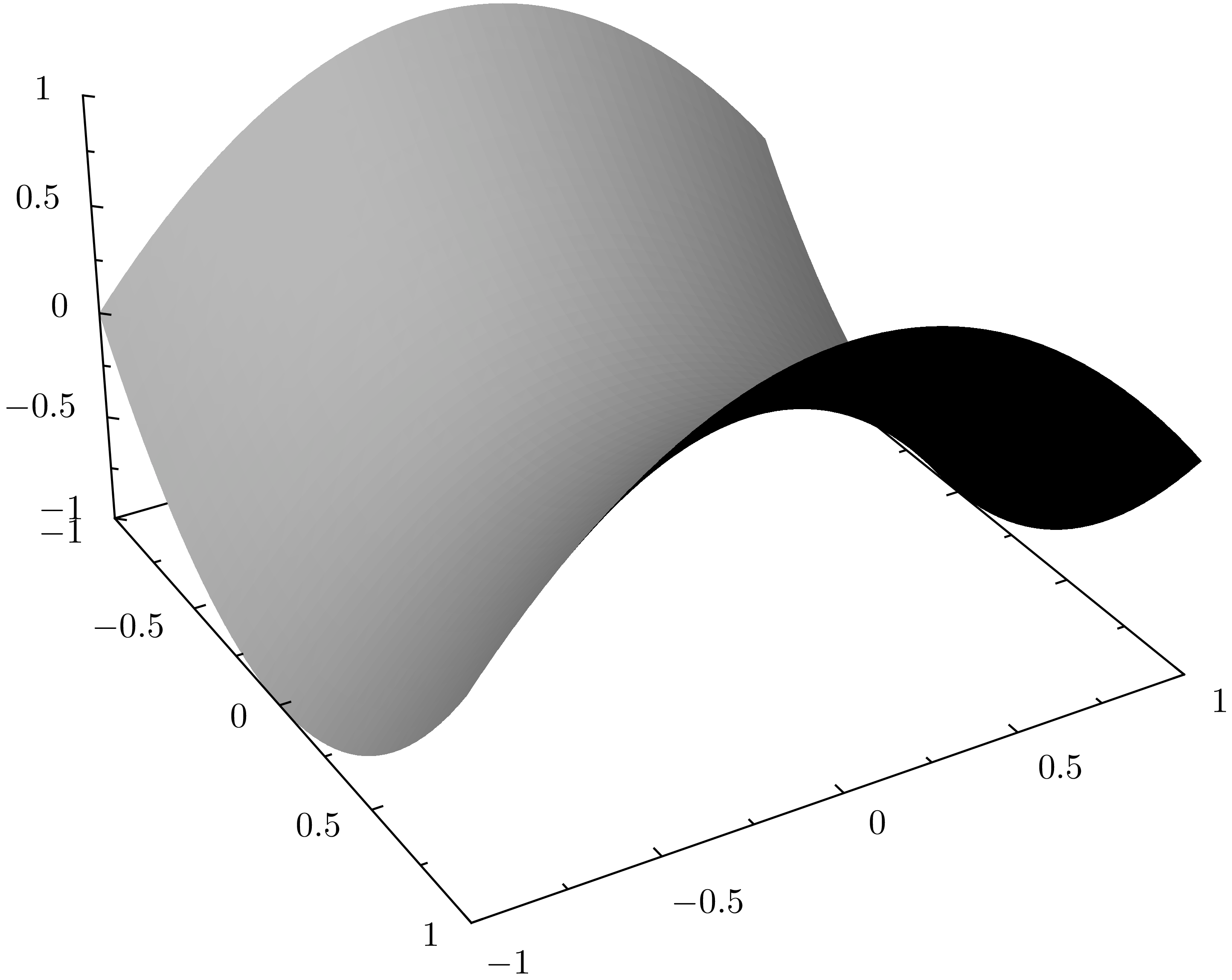
Statt einer grauen Flache kann man auch eine farbige Fläche erhalten, indem man eine geeignete Farbpalette in graph.style.surface mit Hilfe des Arguments gradient übergibt. Wird nichts Weiteres festgelegt, so wird die Farbe auf der Basis des lokalen Funktionswerts gewählt. Wir wollen jedoch in der Farbe noch eine weitere Information kodieren. Dazu erweitern wir die Tupel in unserer Liste data um eine weitere Spalte, die wir in graph.data.points der Farbachse color zuordnen. Außerdem haben wir Achsenbeschriftungen in der gleichen Weise, wie wir das weiter oben schon getan haben, vorgegeben. In graph.style.surface haben wir noch zwei Argumente auf None gesetzt. Mit gridcolor kann eine Farbe für ein Koordinatengitter vorgegeben werden, das auf die Fläche gezeichnet wird. Hier verzichten wir explizit auf ein solches Gitter, auch wenn dies bereits die Defaulteinstellung ist. Zudem verhindern wir mit der Vorgabe für backcolor, dass die Rückseite der Fläche schwarz dargestellt wird wie es im vorigen Beispiel der Fall war.

In [52]: data = [(x, y, x**2-y**2, x**2+y**2)
   ...:          for x in np.linspace(-1, 1, 50) for y in np.linspace(-1, 1, 50)]
   ...: g = graph.graphxyz(size=4,
   ...:                    x=graph.axis.lin(title='$x$'),
   ...:                    y=graph.axis.lin(title='$y$'),
   ...:                    z=graph.axis.lin(title='$x^2-y^2$'))
   ...: g.plot(graph.data.points(data, x=1, y=2, z=3, color=4, title='$x^2+y^2$'),
   ...:        [graph.style.surface(gradient=color.rgbgradient(
   ...:                                            color.gradient.Rainbow),
   ...:                             gridcolor=None,
   ...:                             backcolor=None)])

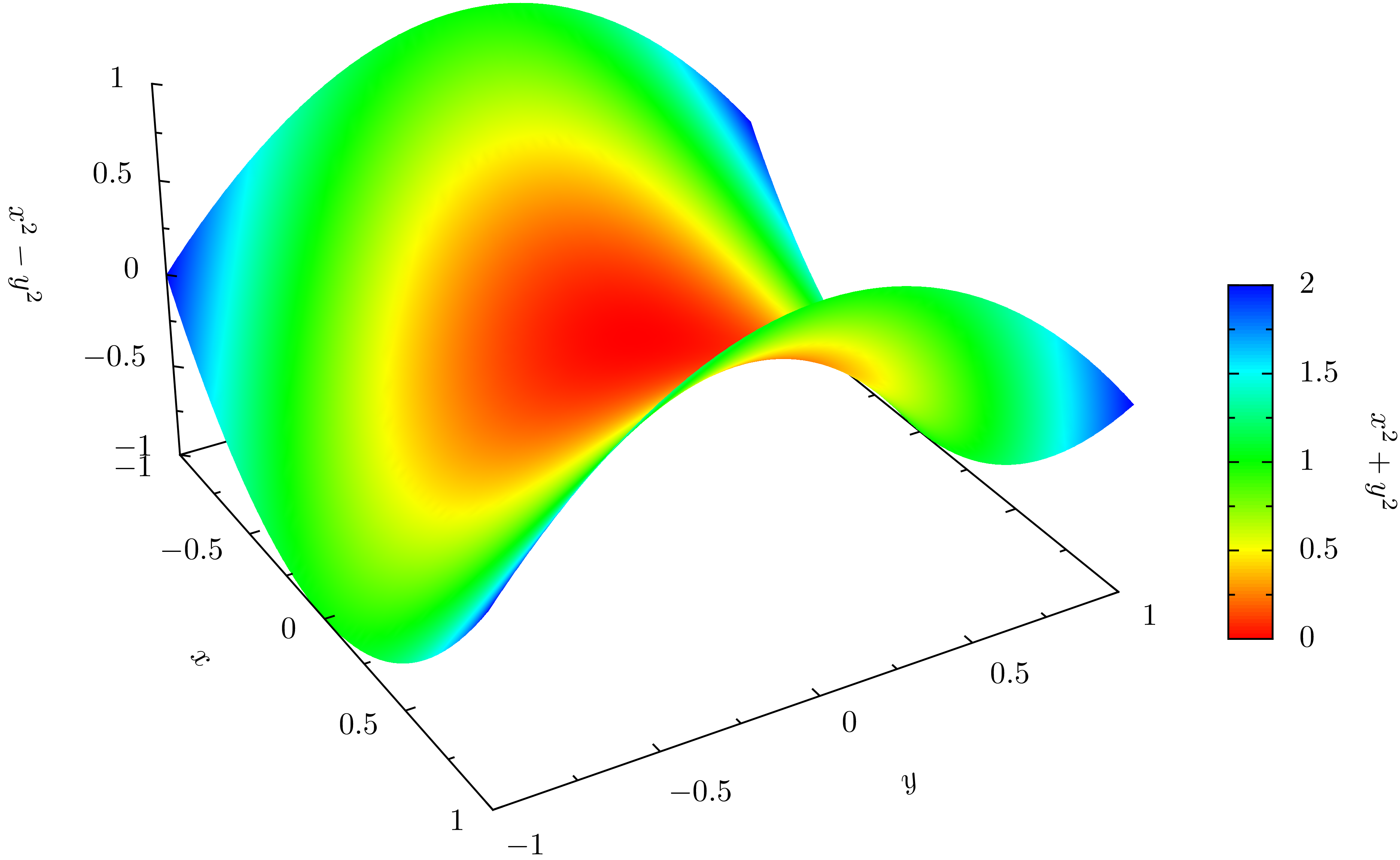
Das nächste Beispiel zeigt, dass man den Blick auf die Fläche den jeweiligen Bedürfnissen anpassen kann. Dazu gibt man im Argument projector des Graphencanvas den entsprechenden Projektor an. Dabei kann es sich um eine Parallelprojektion wie im folgenden Beispiel oder um eine Zentralprojektion wie im übernächsten Beispiel handeln. Bei der Parallelprojektion gibt man den Polarwinkel und den Azimutwinkel für den Normalenvektor auf der x-y-Ebene in Grad an. Bei der Zentralprojektion kommt noch eine Abstandsvariable hinzu.

In [53]: g = graph.graphxyz(size=4,
   ...:                    x=graph.axis.lin(title='$x$'),
   ...:                    y=graph.axis.lin(title='$y$'),
   ...:                    z=graph.axis.lin(title='$x^2-y^2$'),
   ...:                    projector=graph.graphxyz.parallel(-65, 10))
   ...: g.plot(graph.data.points(data, x=1, y=2, z=3, color=4, title='$x^2+y^2$'),
   ...:        [graph.style.surface(gradient=color.rgbgradient(
   ...:                                            color.gradient.Rainbow),
   ...:                             gridcolor=None,
   ...:                             backcolor=None)])

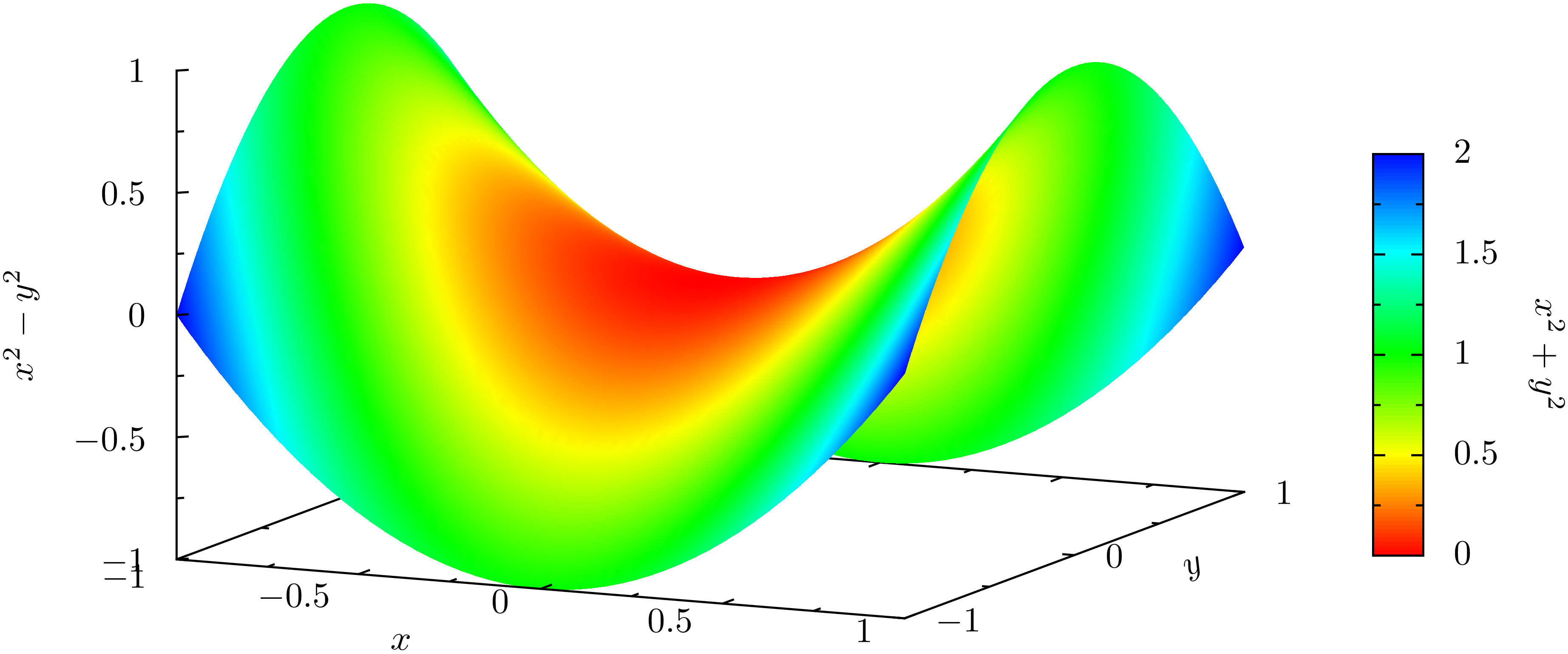
Projektoren kann man auch selbstständig verwenden, um Punkte im dreidimensionalen Raum auf eine Ebene zu projezieren. Der folgende Code berechnet für die Ecken eines Würfels die Projektion in die Ebene, und zeichnet die Achsen und Kanten.

In [54]: import itertools
   ...: projector = graph.graphxyz.central(10, -20, 30).point
   ...: a = 2
   ...: cube = list(itertools.product((-a, a), repeat=3))
   ...: c = canvas.canvas()
   ...: for edge in ((0, 1), (1, 3), (3, 2), (2, 0)):
   ...:     x1, y1 = projector(*cube[edge[0]])
   ...:     x2, y2 = projector(*cube[edge[1]])
   ...:     c.stroke(path.line(x1, y1, x2, y2),
   ...:              [style.linewidth.Thick, color.rgb.red])
   ...:     x1, y1 = projector(*cube[edge[0]+4])
   ...:     x2, y2 = projector(*cube[edge[1]+4])
   ...:     c.stroke(path.line(x1, y1, x2, y2),
   ...:              [style.linewidth.Thick, color.rgb.green])
   ...:     x1, y1 = projector(*cube[edge[0]])
   ...:     x2, y2 = projector(*cube[edge[0]+4])
   ...:     c.stroke(path.line(x1, y1, x2, y2),
   ...:              [style.linewidth.Thick, color.rgb.blue])
   ...: for vertex in cube:
   ...:     x, y = projector(*vertex)
   ...:     c.fill(path.circle(x, y, 0.2))

Dieses Beispiel zeigt noch einmal, wie vielseitig man Grafiken mit PyX erstellen kann, wobei wir hier nur die wichtigsten Aspekte ansprechen konnten. Weitere Informationen findet man in der Dokumentation von PyX auf der Webseite des Projekts.