Allgemeine Vorbemerkungen¶

Python wird immer wieder vorgeworfen, dass es im Vergleich zu einer Reihe anderer Programmiersprachen langsam sei. Häufig stellt dies kein echtes Problem dar, aber bei Bedarf gibt es zur Optimierung von Pythonskripten eine Reihe von Möglichkeiten. Die konsequente Verwendung von NumPy kann bei dazu geeigneten Anwendungen einen erheblichen Geschwindigkeitsvorteil bringen. Unter Umständen kann es auch sinnvoll sein, besonders zeitkritische Programmteile in C zu implementieren. In diesem Fall bietet sich die Verwendung des bereits in einem früheren Kapitel erwähnten Cython an. Mit dessen Hilfe ist es auch sehr einfach möglich, die Rechenzeit durch das Festlegen des Datentyps von Variablen zu reduzieren. Alternativ bietet sich auch die »just in time«-Kompilierung zum Beispiel mit PyPy [2] oder Numba [3] an, die die Programmausführung beschleunigen kann.

Im Einzelfall sollte man zunächst überlegen, ob das Laufzeitproblem wirklich schwerwiegend ist oder ob man für die Optimierung letztlich mehr Zeit investieren muss als man gewinnt. Es lohnt sich dabei, auf den Altmeister Donald E. Knuth zu hören, der schon vor mehr als 40 Jahren schrieb:

There is no doubt that the grail of efficiency leads to abuse. Programmers waste enormous amounts of time thinking about, or worrying about, the speed of noncritical parts of their programs, and these attempts at efficiency actually have a strong negative impact when debugging and maintentance are considered. We should forget about small efficiencies, say about 97 % of the time: premature optimization is the root of all evil.

Yet we should not pass up our opportunities in that critical 3 %. A good programmer will not be lulled into complacency by such reasoning, he will be wise to look carefully at the critical code; but only after that code has been identified. [1]

Bevor man also überhaupt mit der Optimierung eines Programms beginnt, sollte man zunächst immer erst feststellen, wo das Programm die meiste Zeit verbringt. Es lohnt sich nicht, Zeit in die Optimierung von Programmteilen zu investieren, deren Laufzeit im Vergleich zur gesamten Laufzeit unerheblich ist. Nach jeder Optimierung wird man erneut den laufzeitkritischsten Programmteil identifizieren, um so in eventuell mehreren Schritten zu einer hoffentlich akzeptablen Laufzeit zu kommen.

Vor der Optimierung eines Programms sollte man immer bedenken, dass sich dabei Fehler einschleichen können. Es nützt alles nicht, wenn man das Programm geändert hat, so dass es viel schneller läuft, dann aber nicht mehr das tut was es eigentlich tun soll. Daher sollte man mindestens eine funktionstüchtigte Version des Programms aufbewahren, z.B. eine Kopie, die eine Endung .bak erhält. Wesentlich besser ist es natürlich, ein Versionskontrollsystem zu verwenden, beispielsweise Git, das wir im Kapitel Versionskontrolle mit Git beschrieben haben. Außerdem ist es sinnvoll, Tests zu programmieren, die es erlauben, die neue Programmversion auf Korrektheit zu überprüfen. Techniken hierfür werden im Kapitel Testen von Programmen besprochen.

Bevor wir einige Möglichkeiten diskutieren, die Laufzeit von Python-Skripten zu bestimmen, wollen wir im nächsten Abschnitt zunächst auf einige Schwierigkeiten bei der Laufzeitmessung hinweisen.

Fallstricke bei der Laufzeitmessung¶

Python stellt mit dem Modul time eine Möglichkeit zur Verfügung, die aktuelle Zeit und damit letztlich auch Zeitdifferenzen zu bestimmen.

In [1]: import time

In [2]: time.ctime()
Out[2]: 'Thu Dec 22 14:39:30 2016'

Auch wenn die aktuelle Zeit hier in einem gut lesbaren Format ausgegeben wird, eignet sich dieses Ergebnis nur schlecht zur Bildung von Zeitdifferenzen. Besser ist es, die Zahl der Sekunden seit Beginn der „Zeitrechnung“ zu bestimmen. Dabei beginnt die Zeitrechnung auf Unix-Systemen am 1.1.1970 um 00:00:00 UTC.

In [3]: time.time()
Out[3]: 1482413973.190686

Damit lässt sich nun die Zeit bestimmen, die ein bestimmter Python-Code benötigt, wie folgendes Beispiel zeigt.

1
2
3
4
5
6
7
8

import time

summe = 0
start = time.time()
for n in range(1000000):
    summe = summe+1
ende = time.time()
print('{:5.3f}s'.format(ende-start))

Hier wird die Zeitdauer gemessen, die die Schleife in den Zeilen 5 und 6 benötigt. Allerdings ist diese Zeit keineswegs immer genau gleich lang. Das um eine Schleife erweiterte Skript

1
2
3
4
5
6
7
8
9

import time

for _ in range(10):
    summe = 0
    start = time.time()
    for n in range(1000000):
        summe = summe+1
    ende = time.time()
    print('{:5.3f}s'.format(ende-start), end='  ')

liefert zum Beispiel die folgende Ausgabe

0.150s  0.108s  0.104s  0.103s  0.107s  0.106s  0.104s  0.103s  0.103s  0.103s

wobei das Ergebnis beim nächsten Lauf oder erst recht auf einem anderen Computer deutlich anders aussehen kann. Es kann also sinnvoll sein, über mehrere Durchläufe zu mitteln, wie es das timeit-Modul tut, das wir im nächsten Abschnitt besprechen werden.

Bei der Ermittlung von Laufzeiten ist weiter zu bedenken, dass der Prozessor auch von anderen Aufgaben in Anspruch genommen wird, so dass wir gerade zwar die während des Laufs verstrichene Zeit bestimmt haben, nicht aber die Zeit, die der Prozessor hierfür tatsächlich aufgewendet hat. Dies illustrieren wir im folgenden Beispiel, in dem wir das Skript zeitweilig pausieren lassen. Damit wird in Zeile 9 simuliert, dass andere Prozesse für eine Unterbrechung der Ausführung unseres Skripts sorgen. Außerdem benutzen wir in den Zeilen 5 und 11 time.process_time(), um die vom Prozessor aufgewandte Zeit für den Prozess zu bestimmen, in dem unser Skript abgearbeitet wird.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

import time

summe = 0
start = time.time()
start_proc = time.process_time()
for n in range(10):
    for m in range(100000):
        summe = summe+1
    time.sleep(1)
ende = time.time()
ende_proc = time.process_time()
print('Gesamtzeit: {:5.3f}s'.format(ende-start))
print('Systemzeit: {:5.3f}s'.format(ende_proc-start_proc))

Die Ausgabe

Gesamtzeit: 10.248s
Systemzeit: 0.238s

zeigt, dass die Gesamtdauer des Skripts erwartungsgemäß um etwa 10 Sekunden länger ist als die in Anspruch genommene Prozessorzeit.

Vorsicht ist auch geboten, wenn man den zu testenden Codeteil der Übersichtlichkeit halber in eine Funktion auslagert, da dann die Zeit für den Funktionsaufruf relevant werden kann. Dies ist besonders der Fall, wenn die eigentliche Auswertung der Funktion nur sehr wenig Zeit erfordert. So liefert der folgende Code

1
2
3
4
5
6
7
8

import time

summe = 0
start_proc = time.process_time()
for n in range(10000000):
    summe = summe+1
ende_proc = time.process_time()
print('Systemzeit: {:5.3f}s'.format(ende_proc-start_proc))

eine Laufzeit von 1,122 Sekunden, während der äquivalente Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

import time

def increment_by_one(x):
    return x+1

summe = 0
start_proc = time.process_time()
for n in range(10000000):
    increment_by_one(summe)
ende_proc = time.process_time()
print('Systemzeit: {:5.3f}s'.format(ende_proc-start_proc))

mit 1,529 Sekunden gemessen wurde und somit um fast 40 Prozent langsamer läuft.

Unabhängig von den genannten Problemen bedeutet jede Laufzeitmessung immer einen Eingriff in die Ausführung des Skripts, so dass die gemessene Laufzeit unter Umständen deutlich gegenüber der normalen Laufzeit des entsprechenden Codes erhöht sein kann.

Die in den Beispielen verwendete Methode der Laufzeitbestimmung hat Nachteile. Unter anderem erfordert sie eine explizite Modifizierung des Codes, was häufig unerwünscht ist. Im Folgenden besprechen wir einige ausgewählte Alternativen, die entsprechend den jeweiligen Erfordernissen eingesetzt werden können.

Das Modul timeit¶

Um die Laufzeit von Einzeilern oder kleineren Codeteilen zu testen, kann man das Python-Modul timeit heranziehen. Dies ist zum Beispiel dann nützlich, wenn man sich ein Bild davon machen möchte, welche Codevariante die schnellere sein wird. Im Allgemeinen wird dabei über mehrere oder sogar viele Wiederholungen gemittelt, um zu einem möglichst zuverlässigen Ergebnis zu kommen. Die wohl einfachste Möglichkeit, timeit einzusetzen, besteht in der Benutzung der IPython-Shell.

Einen Laufzeitvergleich zwischen zwei Arten eine Zahl zu quadrieren, kann man in IPython folgendermaßen vornehmen:

In [1]: n = 5

In [2]: %timeit n*n
10000000 loops, best of 3: 166 ns per loop

In [3]: %timeit n**2
1000000 loops, best of 3: 252 ns per loop

Das Prozentzeichen wird timeit vorangestellt, um es als so genannten »magischen Befehl« zu kennzeichnen, also einen Befehl der IPython-Shell und nicht ein Python-Kommando. Da timeit in diesem Fall nicht als Python-Kommando interpretiert werden kann, könnte man sogar auf das Prozentzeichen verzichten. Es zeigt sich, dass die Quadrierung durch Multiplikation mit 166 Nanosekunden schneller ausgeführt wird als die Quadrierung durch Potenzierung, die 252 Nanosekunden benötigt. Natürlich hängt die Laufzeit vom verwendeten Prozessor ab und ist auch nicht unbedingt auf die letzte Stelle genau reproduzierbar.

Wie in der Ausgabe dieses Beispiels zu sehen ist, wird der Befehl, dessen Laufzeit bestimmt werden soll, mehrfach ausgeführt. Dabei wird die Zahl der Wiederholungen automatisch so bestimmt, dass sich eine vernünftige Gesamtlaufzeit ergibt.

Um die Laufzeit von mehrzeiligem Code zu untersuchen, wendet man den magischen timeit-Befehl auf eine ganze Zelle an, indem man ein zweites Prozentzeichen voranstellt. Dies ist in folgendem Beispiel gezeigt.

In [4]: %%timeit
   ...: summe = 0
   ...: for n in range(1000):
   ...:     summe = summe+n
   ...:
10000 loops, best of 3: 104 us per loop
In [5]: %timeit sum(range(1000))
10000 loops, best of 3: 22.2 us per loop

Im ersten Fall verwenden wir %%timeit mit zwei Prozentzeichen, damit sich dieser Befehl auf die nächsten drei Zeilen und nicht nur die nächste Zeile bezieht. Im zweiten Fall genügt dagegen wiederum %timeit. In diesem Beispiel liegt die Ausführungszeit im Mikrosekundenbereich, wobei die explizite Schleife fast fünfmal mehr Zeit benötigt.

Auch wenn man mit der IPython-Shell sehr bequem die Laufzeit von Codestücken untersuchen kann, mag es gelegentlich notwendig sein, das timeit-Modul direkt in einem Python-Skript einzusetzen. Daher wollen wir uns nun die Anwendung dieses Moduls ansehen.

Das folgende Beispiel untersucht den Laufzeitunterschied bei der Berechnung des Sinus mit Hilfe des math-Moduls und mit NumPy in Abhängigkeit von der Anzahl der Funktionsargumente.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

import numpy as np
import math
import timeit
import matplotlib.pyplot as plt

def f_numpy(nmax):
    x = np.linspace(0, np.pi, nmax)
    result = np.sin(x)

def f_math(nmax):
    dx = math.pi/(nmax-1)
    result = [math.sin(n*dx) for n in range(nmax)]

x = []
y = []
for n in np.logspace(0.31, 6, 20):
    nint = int(n)
    t_numpy = timeit.timeit("f_numpy({})".format(nint),
                            "from __main__ import f_numpy",
                            number=20)
    t_math = timeit.timeit("f_math({})".format(nint),
                            "from __main__ import f_math",
                            number=20)
    x.append(nint)
    y.append(t_math/t_numpy)
plt.plot(x, y)
plt.xscale("log")
plt.show()

Zunächst definieren wir in den Zeilen 6 bis 12 zwei Funktionen, die jeweils den Sinus für eine vorgegebene Anzahl von Argumenten berechnen, einmal mit Hilfe von NumPy und einmal mit Hilfe des math-Moduls. In den Zeilen 16 bis 25 wird für verschiedene Argumentanzahlen die Laufzeit für die beiden Varianten bestimmt. Sehen wir uns einen der Aufrufe zur Laufzeitbestimmung genauer an, konkret den Code in den Zeilen 18 bis 20. Nachdem wir in Zeile 3 das timeit-Modul geladen hatten, können wir in Zeile 18 die timeit-Funktion aus diesem Modul aufrufen. Das erste Argument enthält den auszuführenden Code, in unserem Fall also einfach den Funktionsaufruf von f_numpy.

Nachdem der Code als String zu übergeben ist, können wir problemlos in der gezeigten Weise ein Argument oder auch mehrere übergeben. Da die von timeit aufgerufenen Funktion keinen Zugriff auf den Namensraum des umgebenden Skripts besitzt, würde es nicht funktionieren, das Argument einfach als nint in dem String unterzubringen. Tatsächlich ist nicht einmal die Funktion f_numpy bekannt. Der timeit-Funktion wird daher in Zeile 19 explizit mitgeteilt, dass zunächst aus unserem Hauptskript, auf das mit __main__ Bezug genommen wird, f_numpy zu importieren ist. In Zeile 20 verlangen wir schließlich noch, dass zwanzig Funktionsläufe durchgeführt werden sollen, um eine gemittelte Laufzeit berechnen zu können. Eine automatische Bestimmung einer sinnvollen Zahl von Wiederholungen nimmt timeit hier im Gegensatz zur Verwendung in IPython nicht vor.

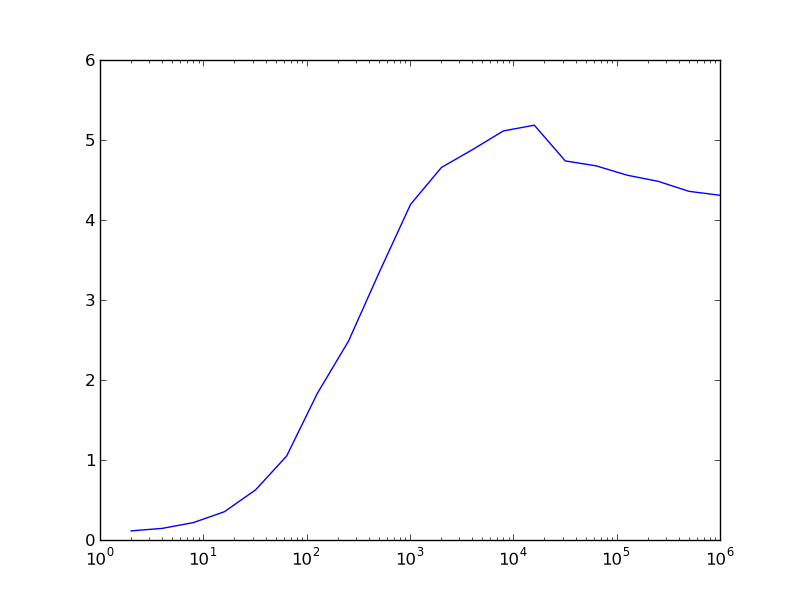
Wie die folgende Abbildung zeigt, bietet NumPy für sehr kleine Argumentanzahlen keinen Geschwindigkeitsvorteil, ganz im Gegenteil. Dies hängt damit zusammen, dass im Zusammenhang mit der Verwendung von Arrays einiges an Zusatzarbeit anfällt. Bei mehr als etwa 100 Argumenten erlaubt NumPy in unserem Fall jedoch eine schnellere Berechnung des Sinus. Der Geschwindigkeitsvorteil kann auf der hier verwendeten Hardware immerhin einen Faktor 4 bis 5 betragen.

Das Modul cProfile¶

Das timeit-Modul, das wir gerade beschrieben haben, ist sehr gut geeignet, um die Laufzeit eines bestimmten Codesegments zu untersuchen. Bei der Optimierung eines Programms interessiert man sich jedoch vor allem dafür, welche Teile des Programms wieviel Zeit benötigen. Dann können die rechenintensiven Codeteile identifiziert und gezielt optimiert werden.

Häufig ist dies jedoch nicht nötig, und es genügt festzustellen, wieviel Zeit in den einzelnen Funktionen oder Methoden verbracht wurde. Dies funktioniert dann besonders gut, wenn man den Code sinnvoll modularisiert, was ja auch im Hinblick auf das Testen von Vorteil ist, wie wir im Kapitel Testen von Programmen betont hatten. Im Folgenden werden wir beschreiben, wie man mit Hilfe des Moduls cProfile feststellen kann, wieviel Zeit in welchen Funktionen während des Programmlaufs verbracht wird.

Als Beispiel ziehen wir das folgende Skript mit Namen pi.py zur Berechnung der Kreiszahl π heran, wobei eine Berechnung auf 100.000 Stellen durchgeführt wird. Das Skript basiert auf dem Gauss-Legendre oder Brent-Salamin-Algorithmus und nutzt aus, dass Python beliebig lange Integers zulässt.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

from math import sqrt

def division(numerator, denominator, stellen):
    resultat = str(numerator//denominator)+"."
    for n in range(stellen):
        numerator = (numerator % denominator)*10
        resultat = "%s%s" % (resultat, numerator//denominator)
    return resultat

def wurzel_startwert(quadrat):
    """bestimme näherungsweise die Wurzel aus einem langen Integer

       Es wird die Wurzel auf der Basis der ersten 12 oder 13 Stellen
       mit Hilfe des entsprechenden Floats gezogen.
    """
    str_quadrat = str(quadrat)
    nrdigits = len(str_quadrat)
    keepdigits = 12
    if nrdigits % 2:
        keepdigits = keepdigits+1
    lead_sqrt_estimate = sqrt(float(str_quadrat[:keepdigits]))
    return int(lead_sqrt_estimate)*10**((nrdigits-keepdigits)//2)+1

def wurzel(quadrat):
    x = wurzel_startwert(quadrat)
    xold = 0
    while x != xold:
        xold = x
        x = (x*x+quadrat)//(2*x)
    return x

def agm_iteration(a, b):
    return (a+b)//2, wurzel(a*b)

def ausgabe(x, zeilenlaenge=80):
    str_x = "\u03c0="+str(x)+"\u2026"
    while len(str_x) > 0:
        print(str_x[:zeilenlaenge])
        str_x = str_x[zeilenlaenge:]

stellen = 100000
skalenfaktor = 10**(stellen+6)
a = skalenfaktor
b = wurzel(skalenfaktor**2//2)
c_sum = 0
faktor_two = 2
while a != b:
    a, b = agm_iteration(a, b)
    faktor_two = faktor_two*2
    c_sum = c_sum+faktor_two*(a*a-b*b)
numerator = 4*a**2
denominator = skalenfaktor**2-c_sum
ergebnis = division(numerator, denominator, stellen)
ausgabe(ergebnis)

Die gesamte Ausgabe ist zu lang, um sie hier vollständig wiederzugeben, so dass wir uns auf die ersten beiden Zeilen beschränken.

π=3.1415926535897932384626433832795028841971693993751058209749445923078164062862
08998628034825342117067982148086513282306647093844609550582231725359408128481117

Von den verschiedenen Varianten, cProfile zu benutzen, wählen wir hier eine, bei der wir das zu untersuchende Programm nicht modifizieren müssen. Dazu rufen wir das Modul mit geeigneten Argumenten auf:

$ python -m cProfile -o pi.prof pi.py

Hierbei wird das Programm pi.py unter der Kontrolle des cProfile-Moduls ausgeführt. Die Option -o legt fest, dass die Ergebnisse in der Datei pi.prof gespeichert werden sollen. Dabei handelt es sich um eine Binärdatei, die mit Hilfe des pstats-Moduls analysiert werden kann. Dazu geht man folgendermaßen vor:

In [1]: import pstats

In [2]: p = pstats.Stats('pi.prof')

In [3]: p.sort_stats('time').print_stats(8)
Fri Dec 23 15:36:56 2016    pi.prof

         2882 function calls in 68.377 seconds

   Ordered by: internal time
   List reduced from 76 to 8 due to restriction <8>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
       18   41.008    2.278   49.819    2.768 pi.py:27(wurzel)
        1   17.776   17.776   17.776   17.776 pi.py:4(division)
       18    8.812    0.490    8.812    0.490 pi.py:12(wurzel_startwert)
        1    0.424    0.424   68.377   68.377 pi.py:1(<module>)
       17    0.320    0.019   47.346    2.785 pi.py:36(agm_iteration)
        1    0.024    0.024    0.037    0.037 pi.py:40(ausgabe)
     1251    0.011    0.000    0.011    0.000 {built-in method builtins.print}
     1270    0.002    0.000    0.002    0.000 {built-in method builtins.len}

Out[3]: <pstats.Stats at 0x7f1a26ed4ac8>

Nachdem in Eingabe 1 das pstats-Modul geladen wurde, wird in Eingabe 2 die zuvor erzeugte binäre Datei pi.prof eingelesen. Man erhält so eine pstats.Stats-Instanz, die nun analysiert werden kann. In den meisten Fällen wird man die Daten nach der benötigten Zeit sortieren und auch nur die obersten Datensätze ausgeben wollen, da die Gesamtliste unter Umständen recht lang sein kann. In Eingabe 3 sortieren wir mit der sort_stats-Methode nach der Zeit, die in der jeweiligen Funktion verbracht wurde. Anschließend wird mit der print_stats-Methode dafür gesorgt, dass nur die ersten acht Zeilen ausgegeben werden.

Das Schlüsselwort time in der sort_stats-Methode verlangt eine Sortierung nach der Zeit, die in der jeweiligen Funktion verbracht wurde. Wird von einer Funktion aus eine andere Funktion aufgerufen, so wird die Uhr für die aufrufende Funktion angehalten. Dies ist zum Beispiel in der Funktion wurzel der Fall, die in Zeile 25 die Funktion wurzel_startwert aufruft. Für die Funktion wurzel wurde gemäß der obigen Ausgabe eine Zeit tottime von 41,008 Sekunden gemessen. Diese enthält nicht die 8,812 Sekunden, die von wurzel_startwert benötigt werden. Die von wurzel benötigte Gesamtzeit lässt sich in der Spalte cumtime (cumulative time, also aufsummierte Zeit) zu 49,819 Sekunden ablesen. Dies entspricht bis auf einen Rundungsfehler der Summe der Zeiten, die in wurzel und wurzel_startwert verbracht wurden. Ist man an den aufsummierten Zeiten interessiert, so kann man das Schlüsselwort cumtime in der sort_stats-Methode verwenden.

In [4]: p.sort_stats('cumtime').print_stats(8)
Fri Dec 23 15:36:56 2016    pi.prof

         2882 function calls in 68.377 seconds

   Ordered by: cumulative time
   List reduced from 76 to 8 due to restriction <8>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    0.000    0.000   68.377   68.377 {built-in method builtins.exec}
        1    0.424    0.424   68.377   68.377 pi.py:1(<module>)
       18   41.008    2.278   49.819    2.768 pi.py:27(wurzel)
       17    0.320    0.019   47.346    2.785 pi.py:36(agm_iteration)
        1   17.776   17.776   17.776   17.776 pi.py:4(division)
       18    8.812    0.490    8.812    0.490 pi.py:12(wurzel_startwert)
        1    0.024    0.024    0.037    0.037 pi.py:40(ausgabe)
     1251    0.011    0.000    0.011    0.000 {built-in method builtins.print}

Out[4]: <pstats.Stats at 0x7f1a26ed4ac8>

Die Ausgabe zeigt auch, dass es nicht immer auf die Zeit ankommt, die pro Aufruf einer Funktion benötigt wird. Diese Information findet sich in der Spalte percall. So benötigt division in unserem Beispiel 17,776 Sekunden je Aufruf, während wurzel nur 2,278 Sekunden je Aufruf benötigt. Allerdings wird division nur einmal aufgerufen, während wurzel achtzehnmal aufgerufen wird. Damit ist der Beitrag von wurzel zur Gesamtlaufzeit erheblich größer als der Beitrag von division.

Es kann sinnvoll sein, die in der Spalte ncalls angegebene Anzahl der Aufrufe einer Funktion auf Plausibilität zu überprüfen. Gelegentlich stellt sich dabei heraus, dass eine Funktion unnötigerweise mehrfach aufgerufen wird. So kann es vorkommen, dass eine Funktion in einer Schleife aufgerufen wird, obwohl sich die Funktionsargumente in der Schleife nicht ändern. Eine entsprechende Anpassung des Programms kann dann auf einfache Weise zu einer Beschleunigung führen.

Mit den beschriebenen Ausgaben lässt sich nun feststellen, in welchen Teilen des Programms der größte Anteil der Rechenzeit verstreicht. Man kann sich somit bei der Optimierung des Programms auf diese Teile konzentrieren. Dabei kann es natürlich vorkommen, dass nach einer Optimierung andere Programmteile in den Fokus rücken. Es kann aber auch sein, dass man feststellen muss, dass die meiste Rechenzeit in einem Programmteil benötigt wird, der sich nicht mehr optimieren lässt. Dann muss man sich die Frage stellen, ob es sinnvoll ist, die Optimierungsbemühungen überhaupt fortzusetzen, da eine Optimierung der anderen Programmteile kaum eine Auswirkung auf die Gesamtrechenzeit haben wird. Um die Situation einschätzen zu können, sind Laufzeitanalysen, wie wir sie hier vorgestellt haben, praktisch unerlässlich.

Zeilenorientierte Laufzeitbestimmung¶

Gelegentlich kann es vorkommen, dass die im letzten Abschnitt beschriebene funktionsbasierte Laufzeitauswertung nicht ausreicht, um ein in Hinblick auf die Laufzeit kritisches Codestück zu identifizieren. In diesem Fall kann man zu einer zeilenorientierten Laufzeitmessung greifen. Wir beschreiben hier das von Robert Kern entwickelte Modul line_profiler [4].

Der besseren Übersichtlichkeit wegen empfiehlt es sich, eine zeilenorientierte Laufzeitmessung auf eine einzelne Funktion oder nur wenige Funktionen zu beschränken. Dazu bestimmt man am besten mit den zuvor beschriebenen Methoden die zeitkritischsten Funktionen. Für Funktionen, die mit einem @profile-Dekorator versehen sind, wird eine zeilenorientierte Laufzeitmessung durchgeführt. Wir wollen speziell die Funktionen wurzel und wurzel_startwert betrachten. Der entsprechende Codeteil sieht dann folgendermaßen aus.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

   @profile
   def wurzel_startwert(quadrat):
       str_quadrat = str(quadrat)
       nrdigits = len(str_quadrat)
       keepdigits = 12
       if nrdigits % 2:
           keepdigits = keepdigits+1
       lead_sqrt_estimate = sqrt(float(str_quadrat[:keepdigits]))
       return int(lead_sqrt_estimate)*10**((nrdigits-keepdigits)//2)+1

   @profile
   def wurzel(quadrat):
       x = wurzel_startwert(quadrat)
       xold = 0
       while x != xold:
           xold = x
           x = xold*xold+quadrat
           x = x//(2*xold)
       return x

Der restliche Code bleibt unverändert. Wesentlich sind hier die beiden @profile-Dekoratoren. Für die folgende Diskussion haben wir den Iterationsschritt des Newton-Verfahrens in zwei Zeilen (17 und 18) aufgeteilt. Außerdem haben wir einen Docstring entfernt, der hier nicht wesentlich ist.

Von der Befehlszeile kann man nun das Skript unter Verwendung der zeilenorientierten Laufzeitmessung ausführen:

kernprof -l -v pi.py

kernprof ist der Name eines Skripts, das die Verwendung des Moduls line_profiler automatisiert, wenn man die Option -l angibt. Die Option -v gibt man an, wenn die Ausgabe direkt angezeigt werden soll. In jedem Fall werden die relevanten Daten ähnlich wie beim cProfile-Modul in eine Binärdatei geschrieben. Sofern nicht mit der Option -o etwas anderes angegeben wird, ergibt sich der Name der Datei durch Anhängen der Endung .lprof. In unserem Falle heißt sie also pi.py.lprof. Aus ihr kann man mit

python -m line_profiler pi.py.lprof

die folgende Ausgabe erzeugen:

Timer unit: 1e-06 s

Total time: 8.71038 s
File: pi.py
Function: wurzel_startwert at line 10

Line #      Hits         Time  Per Hit   % Time  Line Contents
==============================================================
    10                                           @profile
    11                                           def wurzel_startwert(quadrat):
    12        18      8621108 478950.4     99.0      str_quadrat = str(quadrat)
    13        18           61      3.4      0.0      nrdigits = len(str_quadrat)
    14        18           20      1.1      0.0      keepdigits = 12
    15        18           39      2.2      0.0      if nrdigits % 2:
    16                                                   keepdigits = keepdigits+1
    17        18          207     11.5      0.0      lead_sqrt_estimate =
                                                       sqrt(float(str_quadrat[:keepdigits]))
    18        18        88949   4941.6      1.0      return int(lead_sqrt_estimate)
                                                       *10**((nrdigits-keepdigits)//2)+1

Total time: 49.5045 s
File: pi.py
Function: wurzel at line 20

Line #      Hits         Time  Per Hit   % Time  Line Contents
==============================================================
    20                                           @profile
    21                                           def wurzel(quadrat):
    22        18      8710713 483928.5     17.6      x = wurzel_startwert(quadrat)
    23        18           31      1.7      0.0      xold = 0
    24       288          898      3.1      0.0      while x != xold:
    25       270          254      0.9      0.0          xold = x
    26       270      3026189  11208.1      6.1          x = xold*xold+quadrat
    27       270     37766390 139875.5     76.3          x = x//(2*xold)
    28        18           31      1.7      0.0      return x

In der Ausgabe zur Funktion wurzel_startwert haben wir die Zeilen 17 und 18 wegen der Zeilenlänge nachträglich umgebrochen. Die Ausgabe zeigt uns in der Funktion wurzel_startwert nun deutlich, welcher Teil der Funktion für die Ausführungsdauer von fast 9 Sekunden verantwortlich ist, nämlich die Umwandlung eines Integers in einen String. Dieser Schritt ist hier erforderlich, um die Zahl der Ziffern in dem Integer quadrat zu bestimmen.

Interessant ist auch die Funktion wurzel, die für einen größten Teil der Laufzeit verantwortlich ist. In den Zeilen 26 und 27 sehen wir, dass der Großteil der Zeit im Newton-Iterationsschritt verbracht wird. Dabei spielt die Berechnung des Quadrats von xold kaum eine Rolle. Es ist vielmehr die Division in Zeile 27, die einen sehr hohen Zeitaufwand erfordert. Zwar ist die Zeit für die Berechnung des Startwerts in Zeile 22 auf einen einzelnen Aufruf bezogen größer, aber nachdem die Division 270-mal aufgerufen wird, ist sie für mehr als Dreiviertel der Laufzeit der Funktion wurzel verantwortlich.

Bei der Programmentwicklung kann es praktisch sein, das Modul line_profiler in IPython zu verwenden. Im Folgenden ist ein Beispiel gezeigt, das einen Vergleich zwischen der Wurzelfunktion aus dem math-Modul und der Wurzelberechnung mit Hilfe des Newton-Verfahrens anstellt.

In [1]: %load_ext line_profiler

In [2]: import math

In [3]: def newton_sqrt(quadrat):
   ...:     x = 1
   ...:     while abs(quadrat-x*x) > 1e-13:
   ...:         x = 0.5*(x*x+quadrat)/x
   ...:     return x
   ...:

In [4]: def comparison(x):
   ...:     sqrt1 = math.sqrt(x)
   ...:     sqrt2 = newton_sqrt(x)
   ...:     print(sqrt1, sqrt2)
   ...:

In [5]: %lprun -f newton_sqrt comparison(500)
22.360679774997898 22.360679774997898
Timer unit: 1e-06 s

Total time: 7e-05 s
File: <ipython-input-3-e6f13bf0d844>
Function: newton_sqrt at line 1

Line #      Hits         Time  Per Hit   % Time  Line Contents
==============================================================
     1                                           def newton_sqrt(quadrat):
     2         1            4      4.0      5.7      x = 1
     3        10           34      3.4     48.6      while abs(quadrat-x*x) > 1e-13:
     4         9           29      3.2     41.4          x = 0.5*(x*x+quadrat)/x
     5         1            3      3.0      4.3      return x

Zunächst lädt man in Eingabe 1 line_profiler als Erweiterung. Nachdem man die nötigen Funktionen definiert und für dieses Beispiel auch noch das math-Modul geladen hat, kann man in Eingabe 5 mit Hilfe von %lprun die zeilenorientierte Laufzeitmessung ausführen. Dazu gibt man mit der Option -f die Funktion an, in der die Laufzeitmessung benötigt wird. Diese Option ersetzt also den @profile-Dekorator. Bei Bedarf kann die Option -f auch mehrfach angegeben werden. Am Ende steht der Aufruf der Funktion, mit der der gewünschte Code ausgeführt wird, hier also comparison(500).

Nachdem wir uns in diesem Kapitel auf die Messung von Laufzeiten konzentriert hatten, sei abschließend noch angemerkt, dass man auch die Entwicklung des Speicherbedarfs während der Ausführung eines Skripts messen kann. Dies ist besonders dann nützlich, wenn man mit größeren Arrays arbeitet oder an die Grenzen des Arbeitsspeichers stößt. Um im Skript zeilenweise die Entwicklung des Speicherbedarfs messen zu können, verwendet man das Modul memory_profiler.