Threads, Prozesse und der GIL¶

Moderne Betriebssysteme erlauben es selbst auf nur einem Rechenkern, verschiedene Vorgänge scheinbar parallel ablaufen zu lassen. Dies geschieht dadurch, dass diese Vorgänge abwechselnd Rechenzeit zugewiesen bekommen, so dass ein einzelner Vorgang normalerweise nicht die Ausführung der anderen Vorgänge über eine längere Zeit blockieren kann.

Dabei muss man zwei Arten von Vorgängen unterscheiden, nämlich Prozesse und Threads. Prozesse verfügen jeweils über ihren eigenen reservierten Speicherbereich und über einen eigenen Zugang zu Systemressourcen. Dies bedeutet aber auch, dass das Starten eines Prozesses mit einem gewissen Aufwand verbunden ist. Ein Prozess startet zunächst einen und anschließend eventuell auch mehrere Threads, um verschiedene Aufgaben zu bearbeiten. Threads unterscheiden sich dabei von Prozessen vor allem dadurch, dass sie einen gemeinsamen Speicherbereich besitzen und den gleichen Zugang zu den Systemressourcen benutzen. Einen Thread zu starten, ist somit deutlich weniger aufwändig als das Starten eines Prozesses.

Da sich Threads einen gemeinsamen Speicherbereich teilen, können sie sehr leicht auf die gleichen Daten zugreifen oder Daten untereinander austauschen. Die Kommunikation von Threads ist also mit wenig Aufwand verbunden. Allerdings birgt der Zugriff auf gemeinsame Daten auch Gefahren. Trifft man nämlich keine geeigneten Vorkehrungen, um das Lesen und Schreiben von Daten in der erforderlichen Reihenfolge zu gewährleisten, kann es dazu kommen, dass ein Thread nicht die richtigen Daten bekommt. Da das Auftreten solcher Fehler davon abhängt, wann genau welcher Thread welche Aufgaben ausführt, sind diese Fehler nicht ohne Weiteres reproduzierbar und daher nicht immer leicht zu identifizieren. Es gibt Techniken wie man den Datenaustausch zwischen Threads in geordnete Bahnen lenken kann, so dass eine parallele Abarbeitung von Threads, das so genannte Multithreading, möglich wird. Wir wollen hier jedoch darauf verzichten, diese Techniken weiter zu diskutieren.

Die am häufigsten verwendete Implementation von Python, nämlich das in C geschriebene CPython, verwendet einen sogenannten Global Interpreter Lock (GIL). Dieser verhindert, dass ein einzelner Python-Prozess mehrere Threads parallel ausführen kann. Es ist zwar durchaus möglich, in Python[1] Multithreading zu verwenden. Dann sorgt aber der GIL dafür, dass die verschiedenen Threads in Wirklichkeit abwechselnd immer wieder Rechenzeit bekommen, so dass nur der Anschein von paralleler Verarbeitung erweckt wird.

Wenn die Abarbeitung eines Programms durch die Rechenzeit begrenzt ist, führt die Verwendung von Multithreading in Python somit zu keiner Beschleunigung. Im Gegenteil wird der Mehraufwand, der durch den Wechsel zwischen verschiedenen Threads entsteht, eher zu einer Verlangsamung des Programms führen. Es gibt jedoch auch Probleme, deren Bearbeitungsgeschwindigkeit durch Ein- und Ausgabevorgänge bestimmt wird. Ein Beispiel wäre ein Programm, das von vielen Webseiten Daten herunterladen muss, um diese zu bearbeiten. Da ein Thread während des Wartens auf Daten ohnehin untätig ist, kann es in einem solchen Fall auch in Python sinnvoll sein, mehrere Threads zu starten, die dann problemlos ihre benötigte Rechenzeit erhalten können.

Da Programme im numerischen Bereich normalerweise nicht durch Ein- und Ausgabe verlangsamt werden, sondern durch die erforderliche Rechenzeit, werden wir uns im Folgenden nicht mit Multithreading beschäftigen, sondern uns auf die Parallelverarbeitung von Daten durch das Starten von mehreren Prozessen (multiprocessing) konzentrieren.

Abschließend sei noch erwähnt, dass Multithreading im numerischen Bereich auch in Python eine Rolle spielen kann, wenn numerische Bibliotheksroutinen zum Einsatz kommen, die beispielsweise in C geschrieben sind und dann nicht mehr unter der Kontrolle des GIL ausgeführt werden müssen. Ein Beispiel hierfür sind eine Reihe von Operationen aus dem Bereich der linearen Algebra bei der Verwendung einer geeignet kompilierten Version von NumPy. Hierzu zählt das mit der Anaconda-Distribution ausgelieferte, mit der Intel® Math Kernel Library (Intel® MKL) kompilierte NumPy. Eine andere Möglichkeit, den GIL zu umgehen, bietet Cython[2], mit dem C-Erweiterungen aus Python-Code erzeugt werden können. Dabei lassen sich Code-Teile, die keine Python-Objekte verwenden, in einem nogil-Kontext außerhalb der Kontrolle des GIL ausführen (siehe auch das Ende des Abschnitts Kontext mit with-Anweisung).

Parallelverarbeitung in Python¶

Die Verwendung von parallelen Prozessen in Python wollen wir anhand eines konkreten Beispiels diskutieren, nämlich der Berechnung der Mandelbrotmenge, die in einer graphischen Darstellung die sogenannten Apfelmännchen ergibt. Die Mandelbrotmenge ist mathematisch als die Menge der komplexen Zahlen \(c\) definiert, für die die durch die Iterationsvorschrift

gegebene Reihe mit dem Anfangselement \(z_0=0\) beschränkt bleibt. Da bekannt ist, dass die Reihe nicht beschränkt ist, wenn \(|z| > 2\) erreicht wird, genügt es, die Iteration bis zu diesem Schwellwert durchzuführen. Die graphische Darstellung wird dann besonders ansprechend, wenn man die Punkte außerhalb der Mandelbrotmenge farblich in Abhängigkeit von der Zahl der Iterationsschritte darstellt, die bis zum Überschreiten des Schwellwerts von \(2\) erforderlich waren. Da die Iterationen für verschiedene Werte von \(c\) vollkommen unabhängig voneinander sind, ist dieses Problem embarrassingly parallel und man kann sehr leicht verschiedenen Prozessen unterschiedliche Werte von \(c\) zur Bearbeitung zuordnen. Am Ende muss man dann lediglich alle Ergebnisse einsammeln und graphisch darstellen.

Wir beginnen zunächst mit einer einfachen Ausgangsversion eines Programms zur Berechnung der Mandelbrotmenge.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

import matplotlib.pyplot as plt
import numpy as np

def mandelbrot_iteration(c, nitermax):
    z = 0
    for n in range(nitermax):
        if abs(z) > 2:
            return n
        z = z**2+c
    return nitermax

def mandelbrot(xmin, xmax, ymin, ymax, npts, nitermax):
    data = np.empty(shape=(npts, npts), dtype=np.int)
    dx = (xmax-xmin)/(npts-1)
    dy = (ymax-ymin)/(npts-1)
    for nx in range(npts):
        x = xmin+nx*dx
        for ny in range(npts):
            y = ymin+ny*dy
            data[ny, nx] = mandelbrot_iteration(x+1j*y, nitermax)
    return data

def plot(data):
    plt.imshow(data, extent=(xmin, xmax, ymin, ymax),
               cmap='jet', origin='bottom', interpolation='none')
    plt.show()

nitermax = 2000
npts = 1024
xmin = -2
xmax = 1
ymin = -1.5
ymax = 1.5
data = mandelbrot(xmin, xmax, ymin, ymax, npts, nitermax)
# plot(data)

Dabei erfolgt die Auswertung der Iterationsvorschrift in der Funktion mandelbrot_iteration und die Funktion mandelbrot dient dazu, alle Punkte durchzugehen und die Ergebnisse im Array data zu sammeln. Bei der weiteren Überarbeitung ist die Funktion plot nützlich, um die korrekte Funktionsweise des Programms auf einfache Weise testen zu können. Für die Bestimmung der Rechenzeit mit Hilfe des cProfile-Moduls kommentieren wir den Aufruf der plot-Funktion jedoch aus. Die Verwendung von cProfile ist im Kapitel Das Modul cProfile beschrieben. Im Folgenden sind die wesentlichen Beiträge zur Rechenzeit für zwei verschiedene Prozessoren gezeigt, nämlich einen i7-3770:

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
  1048576  306.599    0.000  528.491    0.001 m1.py:4(mandelbrot_iteration)
357051172  221.893    0.000  221.893    0.000 {built-in method builtins.abs}
        1    1.892    1.892  530.383  530.383 m1.py:12(mandelbrot)

und einen i5-4690:

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
  1048576   95.877    0.000  114.408    0.000 m1.py:4(mandelbrot_iteration)
357051172   18.530    0.000   18.530    0.000 {built-in method builtins.abs}
        1    0.424    0.424  114.832  114.832 m1.py:12(mandelbrot)

Es zeigen sich deutliche Unterschiede, wobei aber in beiden Fällen die Berechnung des Absolutbetrags der komplexen Variable z für einen wesentlichen Beitrag zur Rechenzeit verantwortlich ist. Besonders deutlich ist dies im ersten Fall, wo dieser Beitrag über 40 Prozent ausmacht. Allerdings ist bei der Interpretation dieses Ergebnisses etwas Vorsicht geboten, da die Berechnung des Absolutbetrags typischerweise lediglich einige zehn Nanosekunden benötigt, hier aber extrem oft aufgerufen wird. In einer solchen Situation verursacht cProfile einen erheblichen Zusatzaufwand, der sich in den obigen Daten niederschlägt und auch deutlich wird, wenn man die reine Rechenzeit als Differenz von End- und Startzeit bestimmt. Diese liegt für beide Prozessortypen bei etwas 85 Sekunden.

Obwohl also die Berechnung des Absolutbetrags für die Rechenzeit nicht so relevant ist, wie es zunächst den Anschein hat, ist es für spätere Programmversionen sinnvoll, eine reelle Variante der Mandelbrot-Iteration zu implementieren. Damit verfolgen wir die Strategie, bereits vor der Parallelisierung des Programms den Code möglichst stark zu optimieren, um anschließend durch die Parallelisierung einen weitere Beschleunigung des Programms zu erzielen.

Die Berechnung des Absolutbetrags lässt sich vermeiden, wenn man nicht mit einer komplexen Variable rechnet, sondern Real- und Imaginärteil separat behandelt, wie die folgende Version der Funktionen mandelbrot_iteration und mandelbrot zeigt.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

def mandelbrot_iteration(cx, cy, nitermax):
    x = 0
    y = 0
    for n in range(nitermax):
        x2 = x*x
        y2 = y*y
        if x2+y2 > 4:
            return n
        x, y = x2-y2+cx, 2*x*y+cy
    return nitermax

def mandelbrot(xmin, xmax, ymin, ymax, npts, nitermax):
    data = np.empty(shape=(npts, npts), dtype=np.int)
    dx = (xmax-xmin)/(npts-1)
    dy = (ymax-ymin)/(npts-1)
    for nx in range(npts):
        x = xmin+nx*dx
        for ny in range(npts):
            y = ymin+ny*dy
            data[ny, nx] = mandelbrot_iteration(x, y, nitermax)
    return data

Durch diese Umschreibung verkürzt sich die Rechenzeit insbesondere für den i7-3770-Prozessor drastisch:

 ncalls  tottime  percall  cumtime  percall filename:lineno(function)
1048576  121.770    0.000  121.770    0.000 m2.py:4(mandelbrot_iteration)
      1    1.984    1.984  123.754  123.754 m2.py:15(mandelbrot)

Aber auch für den i5-4690-Prozessor ergibt sich eine Verkürzung der Rechenzeit:

 ncalls  tottime  percall  cumtime  percall filename:lineno(function)
1048576   85.981    0.000   85.981    0.000 m2.py:4(mandelbrot_iteration)
      1    0.330    0.330   86.312   86.312 m2.py:15(mandelbrot

Tatsächlich wird diese Verkürzung vor allem durch die Verringerung des durch cProfile bedingten Zusatzaufwands verursacht. Die tatsächliche Rechenzeit kann durch unsere Änderung sogar größer werden. Dennoch ist die Verwendung der reellen Variante in den folgenden Programmversionen günstiger.

Man kann nun vermuten, dass sich die Rechenzeit mit Hilfe von NumPy verringern lässt. In diesem Fall ist eine separate Behandlung der Iteration nicht mehr sinnvoll, so dass wir statt der Funktionen mandelbrot_iteration und mandelbrot nur noch eine Funktion mandelbrot haben, die folgendermaßen aussieht.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def mandelbrot(xmin, xmax, ymin, ymax, npts, nitermax):
    cy, cx = np.mgrid[ymax:ymin:npts*1j, xmin:xmax:npts*1j]
    x = np.zeros_like(cx)
    y = np.zeros_like(cx)
    data = np.zeros(cx.shape, dtype=np.int)
    for n in range(nitermax):
        x2 = x*x
        y2 = y*y
        notdone = x2+y2 < 4
        data[notdone] = n
        x[notdone], y[notdone] = (x2[notdone]-y2[notdone]+cx[notdone],
                                  2*x[notdone]*y[notdone]+cy[notdone])
    return data

Hierbei benutzen wir fancy indexing, da nicht alle Elemente des Arrays bis zum Ende iteriert werden müssen. Es ergibt sich nochmal eine signifikante Reduktion der Rechenzeit. Der i7-3770-Prozessor mit

ncalls  tottime  percall  cumtime  percall filename:lineno(function)
     1   21.066   21.066   21.088   21.088 m3.py:4(mandelbrot)

und der i5-4690-Prozessor mit

ncalls  tottime  percall  cumtime  percall filename:lineno(function)
     1   20.173   20.173   20.191   20.191 m3.py:4(mandelbrot)

unterscheiden sich kaum noch in der benötigten Rechenzeit. Bereits ohne Parallelisierung haben wir durch NumPy mindestens einen Faktor 4 gewonnen.

Nun können wir daran gehen, die Berechnung dadurch weiter zu beschleunigen, dass wir die Aufgabe in mehrere Teilaufgaben aufteilen und verschiedenen Prozessen zur parallelen Bearbeitung übergeben. Seit Python 3.2 stellt die Python-Standardbibliothek hierfür das concurrent.futures-Modul zur Verfügung. Der Name concurrent deutet hier auf das gleichzeitige Abarbeiten von Aufgaben hin, während sich futures auf Objekte beziehen, die zu einem späteren Zeitpunkt das gewünschte Resultat bereitstellen.

Um eine parallele Bearbeitung der Mandelbrotmenge zu ermöglichen, teilen wir den gesamten Wertebereich der zu betrachtenden komplexen Zahlen \(c\) in eine Anzahl von Kacheln auf, die von den einzelnen Prozessen bearbeitet werden. Abb. 1 zeigt, wie 16 Kacheln von vier Prozessen abgearbeitet wurden, wobei jeder Prozess durch eine eigene Frage dargestellt ist. In diesem speziellen Lauf haben zwei Prozesse nur drei Kacheln bearbeitet, während die beiden anderen Prozesse fünf Kacheln bearbeitet haben.

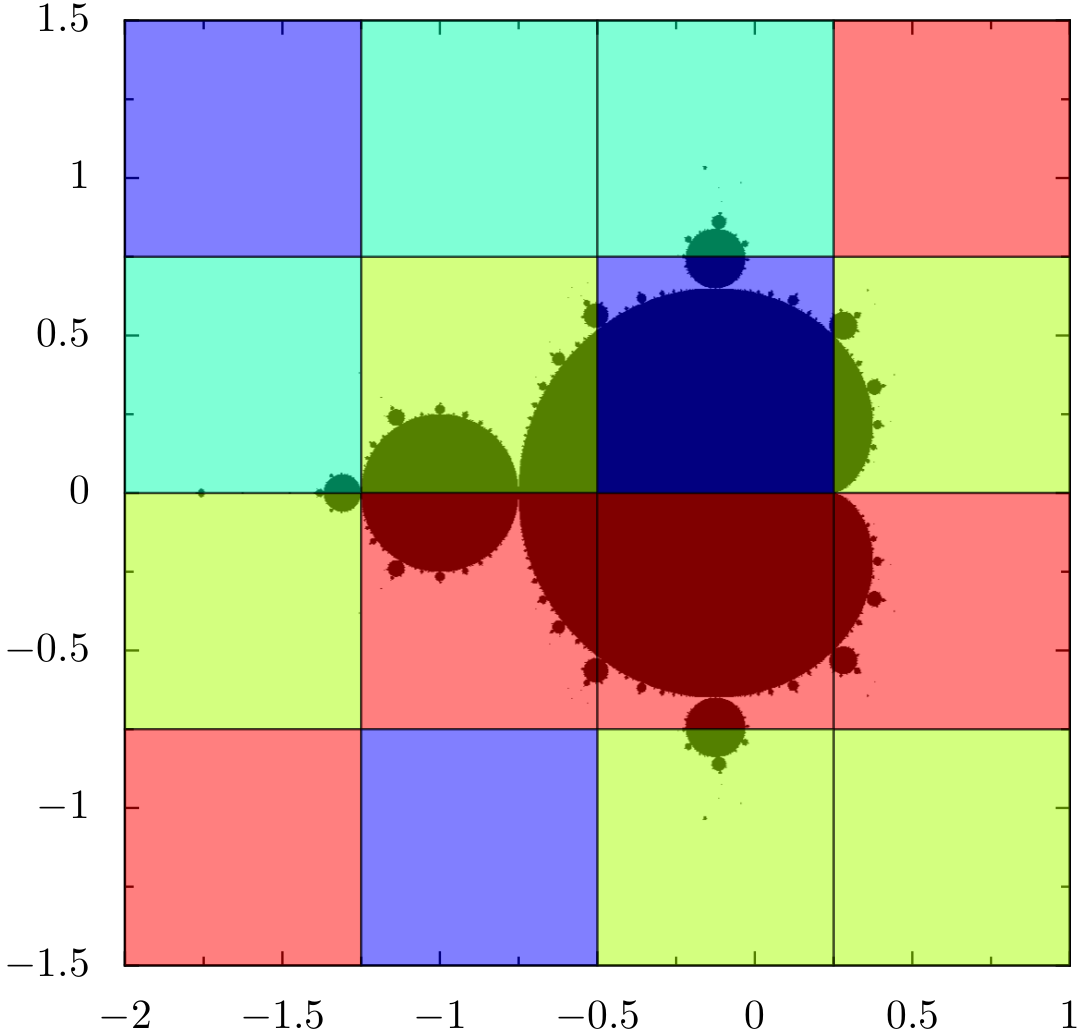
Abb. 1 Bearbeitung der einzelnen Teilbereiche zur Berechnung der Mandelbrotmenge durch vier Prozesse, die durch unterschiedliche Farben gekennzeichnet sind.

Im Folgenden sind die wesentlichen Codeteile dargestellt, die für die parallele Berechnung der Mandelbrotmenge benötigen.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

from concurrent import futures
from itertools import product
from functools import partial
import time

import numpy as np

def mandelbrot_tile(nitermax, nx, ny, cx, cy):
    x = np.zeros_like(cx)
    y = np.zeros_like(cx)
    data = np.zeros(cx.shape, dtype=np.int)
    for n in range(nitermax):
        x2 = x*x
        y2 = y*y
        notdone = x2+y2 < 4
        data[notdone] = n
        x[notdone], y[notdone] = (x2[notdone]-y2[notdone]+cx[notdone],
                                  2*x[notdone]*y[notdone]+cy[notdone])
    return (nx, ny, data)

def mandelbrot(xmin, xmax, ymin, ymax, npts, nitermax, ndiv, max_workers=4):
    start = time.time()
    cy, cx = np.mgrid[ymin:ymax:npts*1j, xmin:xmax:npts*1j]
    nlen = npts//ndiv
    paramlist = [(nx, ny,
                  cx[nx*nlen:(nx+1)*nlen, ny*nlen:(ny+1)*nlen],
                  cy[nx*nlen:(nx+1)*nlen, ny*nlen:(ny+1)*nlen])
                 for nx, ny in product(range(ndiv), repeat=2)]
    with futures.ProcessPoolExecutor(max_workers=max_workers) as executors:
        wait_for = [executors.submit(partial(mandelbrot_tile, nitermax),
                                             nx, ny, cx, cy)
                    for (nx, ny, cx, cy) in paramlist]
        results = [f.result() for f in futures.as_completed(wait_for)]
    data = np.zeros(cx.shape, dtype=np.int)
    for nx, ny, result in results:
        data[nx*nlen:(nx+1)*nlen, ny*nlen:(ny+1)*nlen] = result
    return time.time()-start, data

Die Funktion mandelbrot_tile ist eine leichte Anpassung der zuvor besprochenen Funktion mandelbrot. Der wesentliche Unterschied besteht darin, dass in der vorigen Version das NumPy-Array für die Variable \(c\) in der Funktion selbst erzeugt wurde. Nun werden zwei Arrays mit Real- und Imaginärteil explizit übergeben. Neu ist die Funktion mandelbrot in den Zeilen 21 bis 37. Neben den Grenzen xmin, xmax, ymin und ymax der zu betrachtenden Region, der Zahl der Punkte npts je Dimension und der maximalen Zahl von Iterationen nitermax gibt es noch zwei weitere Variablen. ndiv gibt die Zahl der Unterteilungen je Dimension der Gesamtregion an. Ein Wert von 4 entspricht den 16 Bereichen in der vorigen Abbildung. Die maximale Anzahl von parallelen Prozessen ist durch max_workers gegeben, das wir defaultmäßig auf den Wert 4 setzen, weil wir von einem Prozessor mit vier Kernen ausgehen.

Da wir die Laufzeit bei mehreren parallelen Prozessen nicht mit dem cProfile-Modul bestimmen können, halten wir in Zeile 22 die Startzeit fest und berechnen in Zeile 37 die Laufzeit. Für die Parallelverarbeitung benötigen wir nun zunächst eine Liste von Aufgaben, die durch entsprechende Parameter spezifiziert sind. Dazu werden in Zeile 23 zwei zweidimensionale Arrays angelegt, die das Gitter der komplexen Zahlen \(c\) definieren. Außerdem wird in Zeile 24 die Seitenlänge der Unterbereiche bestimmt. Damit kann nun in den Zeilen 25–28 die Parameterliste erzeugt werden. Hierzu gehen wir mit Hilfe von product aus dem in Zeile 2 importierten itertools-Modul durch alle Indexpaare (nx, ny) der Unterbereiche. Die Parameterliste enthält diese Indizes, die wir später wieder benötigen, um das Resultat zusammenzusetzen, sowie die beiden Arrays mit den zugehörigen Werten des Real- und Imaginärteils von \(c\).

Der zentrale Teil folgt nun in den Zeilen 29 bis 33, wo wir in diesem Fall einen Kontext-Manager verwenden. Dieses Konzept hatten wir im Abschnitt Kontext mit with-Anweisung eingeführt. Es wird ein Pool von Prozessen angelegt, der die Aufgaben ausführen wird, die in Zeile 30 mit Hilfe der zuvor erstellten Parameterliste eingereicht werden. Da die submit-Methode als Argumente eine Funktion sowie deren Argumente erwartet, haben wir hier mit Hilfe des in Zeile 3 importierten functools-Moduls eine partielle Funktion definiert, deren erstes Argument, also nitermax, bereits angegeben ist.

Die Aufgaben werden nun, ohne dass wir uns darum weiter kümmern müssen, nacheinander von den Prozessen abgearbeitet. Wann dieser gesamte Vorgang abgeschlossen sein wird, ist nicht vorhersagbar. Daher wird in Zeile 33 mit Hilfe der Funktion futures.as_completed abgewartet, bis alle Aufgaben erledigt sind. Die Resultate werden in einer Liste gesammelt. Es bleibt nun nur noch, in den Zeilen 34 bis 36 das Ergebnis in einem einzigen Array zusammenzufassen, um es zum Beispiel anschließend graphisch darzustellen.

Es zeigt sich, dass auf den getesteten Prozessoren eine minimale Rechenzeit für die Mandelbrotmenge erreicht wird, wenn das zu behandelnde Gebiet in 64 Teilgebiete unterteilt wird, also sowohl die reelle als auch die imaginäre Achse in acht Segmente unterteilt wird. Dann benötigt ein i7-3770-Prozessor noch etwa 4,4 Sekunden, während ein i5-4690-Prozessor 3 Sekunden benötigt. Damit ergibt sich eine Beschleunigung um einen Faktor von 20 bis 30.

Interessant ist, wie die zeitliche Verteilung der Aufgaben auf die vier Prozesse erfolgt. Dies ist in Abb. 2 für verschiedene Unterteilungen der Achsen zu sehen. Hat man nur vier Aufgaben für vier Prozesse zur Verfügung, so ist die Rechenzeit durch die am längsten laufende Aufgabe bestimmt. Gleichzeitig sieht man bei \(n=2\), dass der Start des Prozesses bei dem in diesem Fall relativ hohen Speicherbedarf zu einer merklichen Verzögerung führt. Ganz grundsätzlich ist der Kommunikationsbedarf beim Starten und Beenden einer Aufgabe in einem Prozess mit einem gewissen Zeitbedarf verbunden. Insofern ist zu erwarten, dass sich zu viele kleine Aufgaben negativ auf die Rechenzeit auswirken. Für \(n=4\) und \(n=8\) beobachten wir aber zunächst eine Verkürzung der Rechenzeit. Dies hängt zum einen damit zusammen, dass jeder Prozess letztlich ähnlich lange für die Abarbeitung seiner Aufgaben benötigt. Bei \(n=4\) ist deutlich zu sehen, dass sich die Anzahl der bearbeiteten Aufgaben von Prozess zu Prozess erheblich unterscheiden kann.

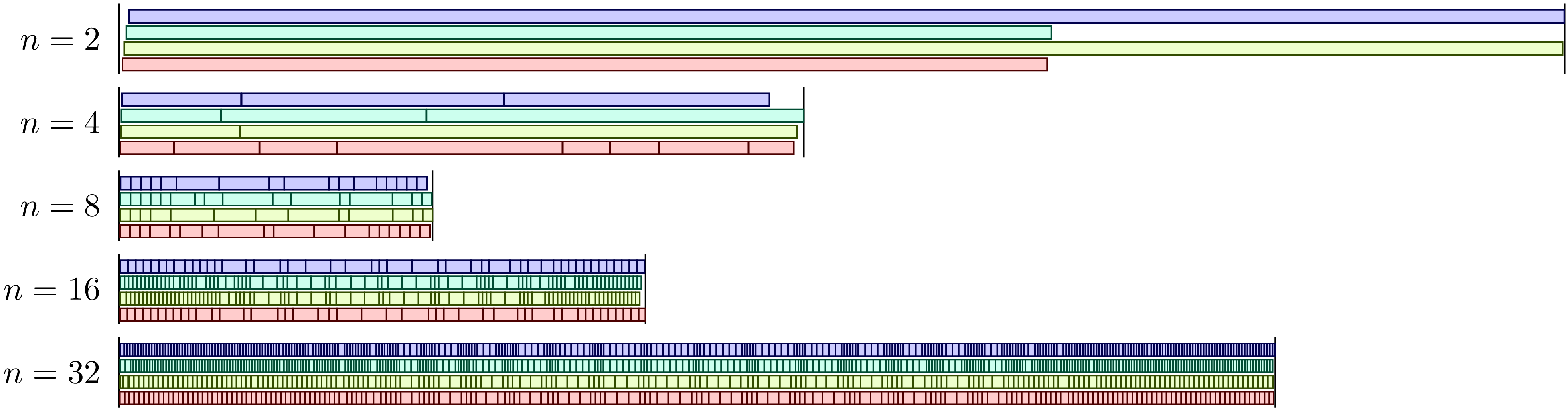
Abb. 2 Verteilung der Teilaufgaben für die Berechnung der Mandelbrotmenge auf vier Prozesse in Abhängigkeit von der Anzahl der Segmente je Achse.

Außerdem wird die Rechenzeit unter Umständen wesentlich durch den Umfang der in einem Prozess zu bearbeitenden Daten bestimmt. Dies hängt damit zusammen, dass die Versorgung des Prozessors mit Daten einen erheblichen Engpass darstellen kann. Aus diesem Grund werden zwischen dem Hauptspeicher und dem Prozessor so genannte Caches implementiert, die einen schnelleren Datenzugriff erlauben, die jedoch in ihrer Größe begrenzt sind. Daher kann es für die Rechengeschwindigkeit förderlich sein, die für die individuelle Aufgabe erforderliche Datenmenge nicht zu groß werden zu lassen.

Dies wird an Abb. 3 deutlich. Betrachten wir zunächst die gestrichelten Kurven, bei denen die Rechenzeit für die Gesamtaufgabe, also für \(n=1\), durch die Rechenzeit für die Parallelverarbeitung für verschiedene Werte von \(n\) geteilt wurde. Obwohl nur vier Prozesse verwendet wurden, findet man unter gewissen Bedingungen eine Beschleunigung, die über dem Vierfachen liegt. Bei den zugehörigen Aufgabengrößen können die Caches offenbar sehr gut genutzt werden. Eine vom Verhalten der Caches unabhängige Einschätzung des Einflusses der Parallelisierung erhält man durch Vergleich der parallelen Abarbeitung der Teilaufgaben mit der sequentiellen Abarbeitung der gleichen Teilaufgaben. Die zugehörige Beschleunigung ist durch die durchgezogenen Kurven dargestellt. Hier zeigt sich, dass ein Verhältnis von vier entsprechend der vier Prozesse nahezu erreicht werden kann, wenn die Größe der Teilaufgaben nicht zu groß gewählt ist.

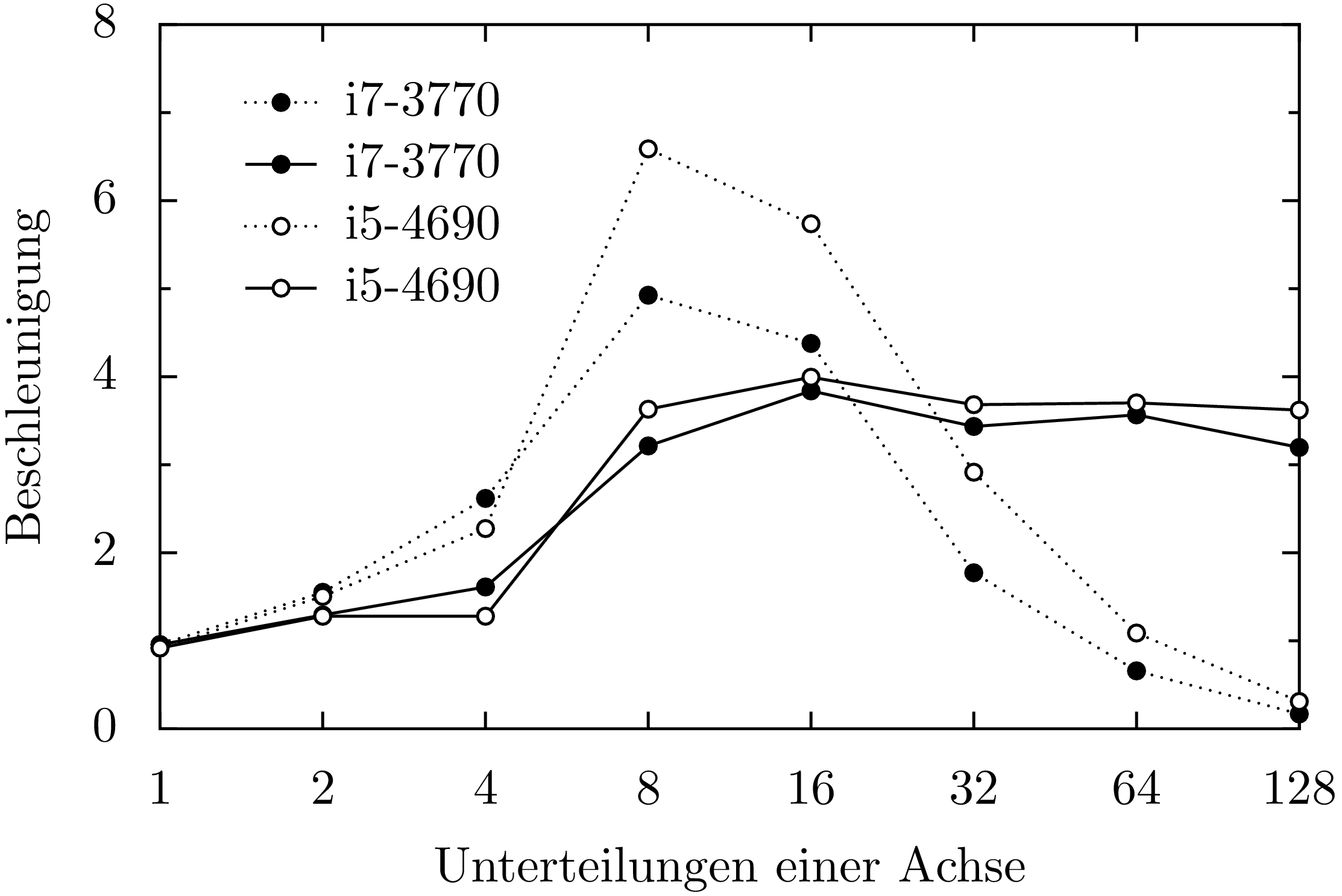
Abb. 3 Die Beschleunigung durch Parallelisierung bei der Berechnung der Mandelbrotmenge ist für die zwei Prozessortypen i7-3770 (schwarze Punkte) und i5-4690 (weiße Punkte) als Funktion der Unterteilung der Achsen dargestellt. Die gestrichelten Kurven zeigen das Verhältnis der Rechenzeit für das Gesamtproblem zur Rechenzeit für die parallelisierte Variante, während die durchgezogenen Kurven das Verhältnis der Rechenzeit für die sequentielle Abarbeitung der Teilaufgaben zur Rechenzeit für die parallele Abarbeitung zeigen.

Numba¶

Im vorigen Abschnitt haben wir gesehen, wie man mit Hilfe von NumPy und durch Parallelisierung ein Programm beschleunigen kann. Dies ging in dem Beispiel der Mandelbrotmenge relativ einfach, da natürlicherweise Arrays verwendet werden konnten und zudem die Behandlung der einzelnen Teilprobleme keine Kommunikation untereinander erforderte. Neben NumPy und der Parallelisierung gibt es noch andere Optionen, um Code zu beschleunigen, die sich zum Teil aktuell sehr intensiv weiterentwickelt werden, so dass sich die Einsatzmöglichkeiten unter Umständen zukünftig schnell erweitern können. Daher soll in diesem Abschnitt auch nur ein Eindruck von anderen Möglichkeiten gegeben werden, ein Programm zu beschleunigen.

Wir greifen hier speziell Numba [3] heraus, da es unter anderem für das numerische Arbeiten im Zusammenhang mit NumPy konzipiert ist und auch Parallelverarbeitung unterstützt. Zentral für Numba ist die sogenannte Just in Time (JIT) Kompilierung. Hierbei werden Funktionen in ausführbaren Code übersetzt, der anschließend schneller ausgeführt werden kann als dies der Python-Intepreter tun würde. Während in Python der Datentyp der Funktionsargumente nicht spezifiziert ist, sieht sich Numba beim Funktionsaufruf die tatsächlich verwendeten Datentypen an und erzeugt entsprechenden ausführbaren Code. Bei nächsten Aufruf mit der gleichen Signatur, also mit den gleichen Datentypen der Argumente, kann auf diesen Code zurückgegriffen werden. Andernfalls wird bei Bedarf eine andere Version des ausführbaren Codes erstellt.

Wir wollen dies an einem einfachen Beispiel illustrieren, in dem näherungsweise die riemannsche Zetafunktion

berechnet wird. Der im folgenden Code implementierte Algorithmus ist nicht optimal für die Berechnung der Zetafunktion, aber dies ist für unser Beispiel nicht relevant. Ohne Verwendung von Numba könnte unser Code wie folgt aussehen:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

import time

def zeta(x, nmax):
    summe = 0
    for n in range(1, nmax+1):
        summe = summe+1/(n**x)
    return summe

nmax = 100000000
start = time.time()
print(zeta(2, nmax))
print('Zeit:', time.time()-start)

Da hier die Summe nur über endlich viele Terme ausgeführt wird sei erwähnt, dass \(\zeta(2)=\pi^2/6\).

Für die Verwendung mit Numba müssen wir lediglich Numba importieren (Zeile 2) und die Funktion mit einem Dekorator (Zeile 4) versehen:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

import time
import numba

@numba.jit
def zeta(x, nmax):
    summe = 0
    for n in range(1, nmax+1):
        summe = summe+1/(n**x)
    return summe

nmax = 100000000
start = time.time()
print(zeta(2, nmax))
print('Zeit:', time.time()-start)

Vergleichen wir die beiden Laufzeiten, so erhalten wir auf dem gleichen Rechner im ersten Fall etwa 33,4 Sekunden, im zweiten Fall dagegen nur 0,6 Sekunden. Wir können uns am Ende dieses Codes anzeigen lassen, welche Signatur von Numba kompiliert wurde, indem wir die folgende Zeile anhängen:

print(zeta.signatures)

Das Ergebnis lautet:

[(int64, int64)]

Diese Liste von Signaturen enthält nur einen Eintrag, da wir die Funktion zeta mit zwei Integer-Argumenten aufgerufen haben. Wie in NumPy können Integers hier nicht beliebig lang werden, sondern sind in diesem Beispiel 8 Bytes lang. Es besteht also die Gefahr des Überlaufs. So kommt es in unserem Beispiel zur einer Division durch Null, wenn man die Variable x auf den Wert :math:3 setzt. Bereits vor der Division durch Null wird aufgrund des Überlaufs durch negative Zahlen dividiert, so dass die Summe unsinnige Werte liefert. Die Gefahr des Überlaufs muss also bedacht werden.

Übergibt man auch Gleitkomma- oder komplexe Zahlen für das Argument x, so muss Numba für diese neuen Signaturen eine Kompilation durchführen. Der Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

import time
import numba

@numba.jit
def zeta(x, nmax):
    summe = 0
    for n in range(1, nmax+1):
        summe = summe+1/(n**x)
    return summe

nmax = 100000000
for x in (2, 2.5, 2+1j):
    start = time.time()
    print('ζ({}) = {}'.format(x, zeta(x, nmax)))
    print('Zeit: {:5.2f}s\n'.format(time.time()-start))

print(zeta.signatures)

liefert die Ausgabe:

ζ(2) = 1.644934057834575
Zeit:  0.59s

ζ(2.5) = 1.341487257103954
Zeit:  5.52s

ζ((2+1j)) = (1.1503556987382961-0.43753086346605924j)
Zeit: 13.41s

[(int64, int64), (float64, int64), (complex128, int64)]

Wir sehen zum einen, dass die Rechendauer vom Datentyp der Variable x abhängt, und zum anderen, dass die Kompilierung in der Tat für drei verschiedene Signaturen durchgeführt wurde.

Mit Hilfe von Numba können wir zudem Funktionen leicht in universelle Funktionen, also ufuncs umwandeln, die wir in Abschnitt Universelle Funktionen im Zusammenhang mit NumPy eingeführt hatten. Universelle Funktionen sind in der Lage, neben skalaren Argumenten auch Arrays als Argumente zu verarbeiten. Dies erlaubt bereits die Verwendung des Dekorators jit. Mit Hilfe des Dekorators vectorize kann zudem erreicht werden, dass die Funktionsauswertung für die Werte des Arrays in mehreren Threads parallel ausgeführt wird.

Im folgenden Codebeispiel geben wir als Argumente für den Dekorator die Signatur an, die Numba verwenden soll. Das Argument x hat den Datentyp float64 und kann auch ein entsprechendes Array sein. Das Argument n ist vom Datentyp int64. Der Datentyp des Resultats ist wiederum float64 und steht als erstes in der Signatur vor dem Klammerpaar, das die Datentypen der Argumenten enthält. Das Argument target bekommt hier den Wert 'parallel', um für ein Array die Parallelverarbeitung in mehreren Threads zu erlauben. Wird eine Parallelverarbeitung nicht gewünscht, zum Beispiel weil das Problem zu klein ist und das Starten eines Threads nur unnötig Zeit kosten würde, so kann man auch target='cpu' setzen. Hat man einen geeigneten Grafikprozessor, so kann dieser mit target='cuda' zur Rechnung herangezogen werden.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

import time
import numpy as np
from numba import vectorize, float64, int64

@vectorize([float64(float64, int64)], target='parallel')
def zeta(x, nmax):
    summe = 0.
    for n in range(nmax):
        summe = summe+1./((n+1)**x)
    return summe

x = np.linspace(2, 10, 200, dtype=np.float64)
start = time.time()
y = zeta(x, 10000000)
print(time.time()-start)

In Abb. 4 ist die Beschleunigung des Programms als Funktion der verwendeten Threads für einen i7-3770-Prozessor gezeigt, der vier Rechenkerne besitzt, auf dem aber durch sogenanntes Hyperthreading acht Threads parallel laufen können. Bei Verwendung von bis zur vier Threads steigt die Beschleunigung fast wie die Zahl der Threads an, während die Beschleunigung darüber merklich langsamer ansteigt. Dies hängt damit zusammen, dass dann Threads häufiger auf freie Ressourcen warten müssen.

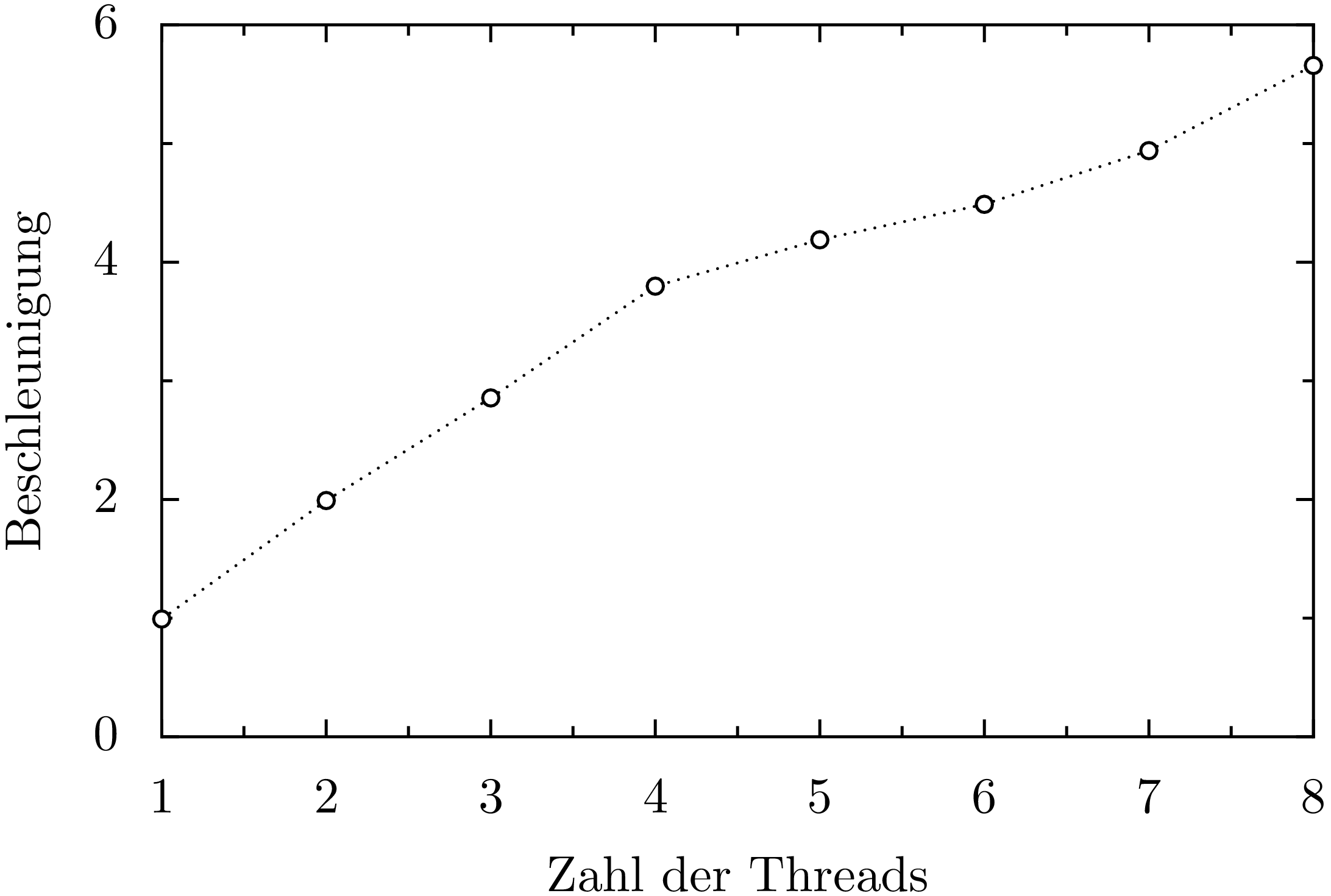
Abb. 4 Beschleunigung der Rechengeschwindigkeit für die Berechnung der Zetafunktion mit dem Quellcode 4 als Funktion der Anzahl der Threads auf einem Vierkernprozessor mit Hyperthreading.

In Numba lassen sich universelle Funktionen mit Hilfe des Dekorators guvectorize noch verallgemeinern, so dass in der inneren Schleife auch Arrays verwendet werden können. Bei den üblichen universellen Funktionen wird in der inneren Schleife dagegen mit Skalaren gearbeitet. Um dies an einem Beispiel zu verdeutlichen, kommen wir auf das Mandelbrotbeispiel zurück.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

import time

from numba import jit, guvectorize, complex128, int64
import matplotlib.pyplot as plt
import numpy as np

@jit
def mandelbrot_iteration(c, maxiter):
    z = 0
    for n in range(maxiter):
        z = z**2+c
        if z.real*z.real+z.imag*z.imag > 4:
            return n
    return maxiter

@guvectorize([(complex128[:], int64[:], int64[:])], '(n), () -> (n)',
             target='parallel')
def mandelbrot(c, itermax, output):
    nitermax = itermax[0]
    for i in range(c.shape[0]):
        output[i] = mandelbrot_iteration(c[i], nitermax)

def mandelbrot_set(xmin, xmax, ymin, ymax, npts, nitermax):
    cy, cx = np.ogrid[ymin:ymax:npts*1j, xmin:xmax:npts*1j]
    c = cx+cy*1j
    return mandelbrot(c, nitermax)

def plot(data, xmin, xmax, ymin, ymax):
    plt.imshow(data, extent=(xmin, xmax, ymin, ymax),
               cmap='jet', origin='bottom', interpolation='none')
    plt.show()

nitermax = 2000
npts = 1024
xmin = -2
xmax = 1
ymin = -1.5
ymax = 1.5
start = time.time()
data = mandelbrot_set(xmin, xmax, ymin, ymax, npts, nitermax)
ende = time.time()
print(ende-start)
plot(data, xmin, xmax, ymin, ymax)

Unser besonderes Augenmerk richten wir hier auf die Funktion mandelbrot, die mit dem guvectorize-Dekorator versehen ist und einige Besonderheiten aufweist. Die Funktion mandelbrot besitzt drei Argumente, von denen hier zwei, nämlich c und itermax, an die Funktion übergeben werden, während das dritte Argument, also output für die Rückgabe des Ergebnisses vorgesehen ist. Dies kann man dem zweiten Argument des Dekorators, dem sogenannten Layout, entnehmen. Diesem kann man entnehmen, dass das zurückgegebene Array output die gleiche Form wie das Argument c besitzt. Da wir ein zweidimensionales Array c übergeben, ist das Argument c[i] der Funktion mandelbrot_iteration selbst wieder ein Array. Andererseits muss man bedenken, dass das Argument itermax ein Array ist, so dass hier zur Verwendung als Skalar das Element 0 herangezogen wird.

Auf einem i7-3770-Prozessor, der durch Hyperthreading bis zu acht Threads unterstützt, wird dieses Programm in knapp 0,48 Sekunden ausgeführt. Wir erreichen somit eine Beschleunigung gegenüber unserem bisher schnellsten Quellcode 3 um fast eine Größenordnung. Gegenüber unserer allerersten Version haben wird auf diesem Prozessortyp sogar eine Beschleunigung um einen Faktor von fast 200 erreicht.