matplotlib¶

Nachdem SciPy/NumPy keine grafischen Fähigkeiten besitzt, wird in diesem Umfeld zur Erzeugung von Grafiken häufig matplotlib empfohlen, das unter anderem auf den Array-Datentyp von NumPy zurückgreift. matplotlib kann auf zwei verschiedene Arten verwendet werden. Zum einen kann man mit Hilfe des Python-Interpreters durch direkte Eingabe von Kommandos schnell Grafiken erzeugen. Zum anderen kann man Grafiken aber auch mit einem vollständigen Python-Programm erstellen. Letzteres ist vor allem dann sinnvoll, wenn man Eigenschaften der Grafik im Detail festlegen will. Wir beginnen zunächst mit der ersten Variante und betrachten ein Beispiel, in dem zwei Besselfunktionen unter Verwendung von SciPy dargestellt werden.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.special import j0, j1
>>> x = np.arange(0, 50, 0.2)
>>> y1 = j0(x)
>>> y2 = j1(x)
>>> plt.plot(x, y1)
[<matplotlib.lines.Line2D object at 0xa273f0c>]
>>> plt.plot(x, y2)
[<matplotlib.lines.Line2D object at 0xa2732cc>]
>>> plt.show()

In Zeile 1 wird zunächst das NumPy-Paket geladen, um in Zeile 4 ein Array mit x-Werten erzeugen zu können. Anschließend wird in Zeile 2 die Plot-Funktionalität von matplotlib, soweit sie im Folgenden benötigt wird, geladen [4]. Auch hier wird, wie schon bei NumPy, eine übliche Abkürzung eingeführt, um Tipparbeit zu sparen. Schließlich werden in der Zeile 3 zwei Besselfunktionen aus SciPy importiert, die im Weiteren dargestellt werden sollen. In Zeile 4 wird nun, wie schon angedeutet, ein Array mit den x-Werten erzeugt, für die in den folgenden beiden Zeilen Arrays mit den Besselfunktionen \(J_0(x)\) und \(J_1(x)\) berechnet werden. In den Zeilen 7-10 werden dann die beiden Funktionsgraphen erzeugt. Wie die Zeilen 8 und 10 andeuten, handelt es sich dabei um matplotlib.lines.Line2D-Objekte. Abschließend erfolgt die Darstellung des Graphen in Zeile 11. Die Ausgabe erfolgt auf den Bildschirm, wo die Grafik in einem Fenster, wie in der folgenden Abbildung gezeigt, dargestellt wird.

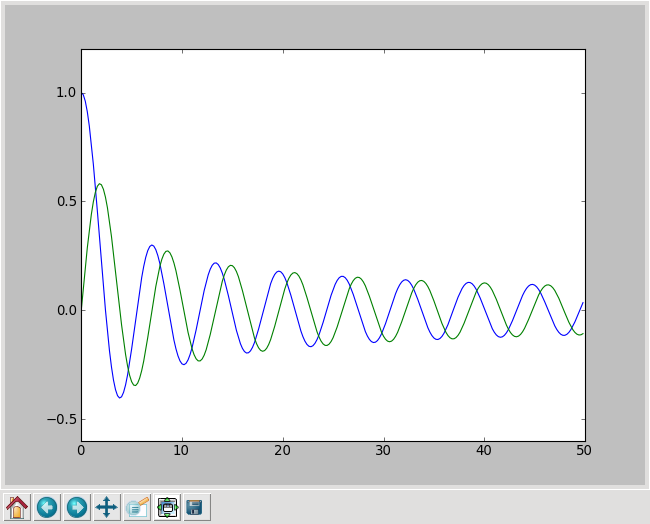
Die Knöpfe am linken unteren Rand des Fensters kann man benutzen, um zum Beispiel in die Grafik hineinzuzoomen wie es die folgende Abbildung zeigt oder den dargestellten Ausschnitt zu verschieben.

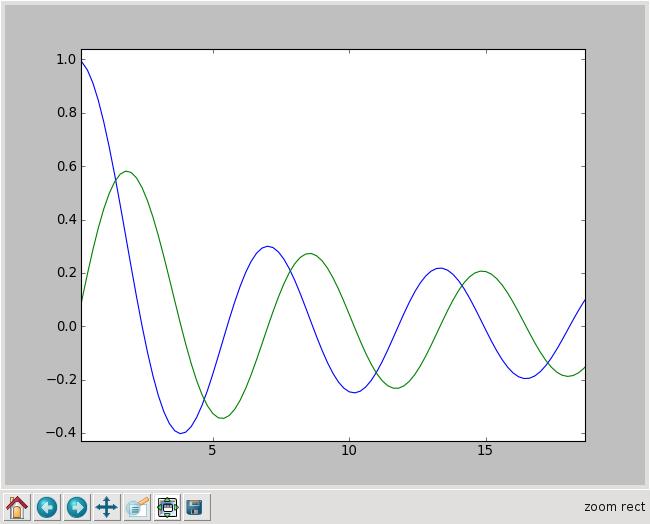
Mit dem Haussymbol kommt man immer wieder zu der ursprünglichen Darstellung zurück.

Alternativ zu dieser interaktiven Arbeitsweise kann man Grafiken auch mit Hilfe eines normalen Python-Programms erzeugen. Als Beispiel wollen wir ein Programm betrachten, das eine Zufallsbewegung berechnet und darstellt.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

import numpy as np
from numpy.random import rand
import matplotlib.pyplot as plt
from math import pi

npts = 10000
r = 0.1
for _ in range(3):
    x = np.zeros(npts+1)
    y = np.zeros(npts+1)
    richtung = 2*pi*rand(npts)
    x[1:] = np.cumsum(r*np.cos(richtung))
    y[1:] = np.cumsum(r*np.sin(richtung))
    plt.plot(x, y)

plt.xlabel("x")
plt.ylabel("y")
plt.savefig("randomwalk.pdf")

In den ersten vier Zeilen werden zunächst wieder wie gewohnt Module importiert, wobei in Zeile 2 eine Funktion zur Erzeugung von Zufallszahlen aus NumPy importiert wird. Die Zufallsbewegung wird nun in einer diskreten Weise durch npts Punkte spezifiziert, wobei jeweils ein Schritt der Länge r in eine Zufallsrichtung, die durch ein Element des Arrays richtung festgelegt ist, ausgeführt wird. Diese Schritte werden in den Zeilen 12 und 13 kumulativ aufsummiert, um die Trajektorien zu erzeugen. Durch die Zeilen 9 und 10 und die verschobene Indizierung in den Zeilen 12 und 13 wird dafür gesorgt, dass alle Trajektorien im Ursprung starten. Die durch die Werte in x und y definierte Trajektorie wird in Zeile 14 geplottet. Insgesamt wird dieser Vorgang mit Hilfe der for-Schleife dreimal durchgeführt. Abschließend wird noch eine Achsenbeschriftung hinzugefügt und schließlich die Abbildung in einer PDF-Datei abgespeichert, die im Folgenden dargestellt ist.

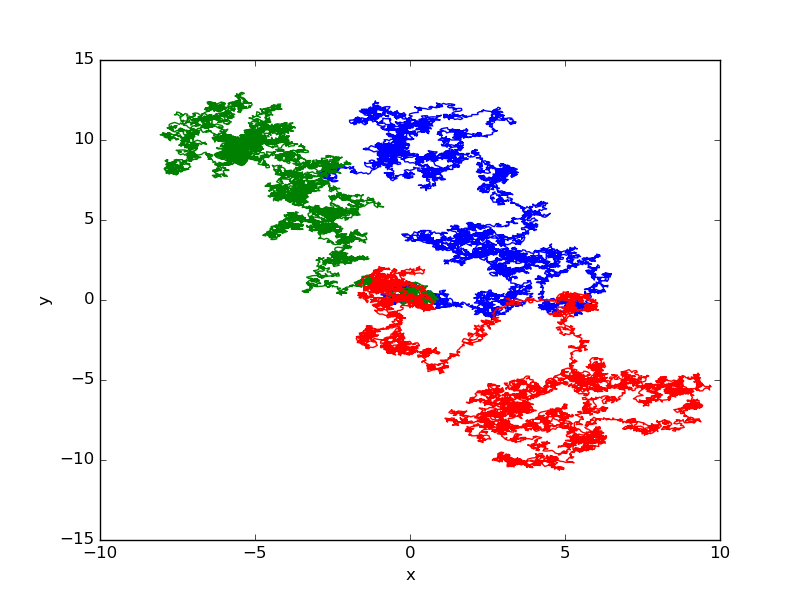
Hier stellt man fest, dass matplotlib automatisch die Farbe der Linien wechselt. Alternativ hätte man die Farben auch explizit spezifizieren können.

PyX¶

Eine mögliche Alternative zu matplotlib stellt PyX dar, das von André Wobst und Jörg Lehmann, in der Anfangsphase der Programmentwicklung als Doktoranden am Lehrstuhl für Theoretische Physik I der Universität Augsburg tätig, programmiert wurde und noch weiterentwickelt wird. Etwas später kam noch Michael Schindler hinzu. Die drei Buchstaben in PyX stehen für »Postscript«, »Python« und »(La)TeX« [5]. Postscript wurde als Ausgabeformat inzwischen noch durch PDF erweitert. PyX ist in Python geschrieben und wird zur Erzeugung von Grafiken in Python-Programme importiert. Zudem lassen sich bei Bedarf in Python eigene Erweiterungen programmieren. (La)TeX schließlich wird für eine qualitativ hochwertige Textausgabe benutzt, wobei matplotlib ähnliche Möglichkeiten bietet. Seit Version 0.13 läuft PyX ausschließlich unter Python 3.

Mit PyX lassen sich nicht nur Graphen erstellen, sondern auch Schemazeichnungen erzeugen. So wurden die meisten Abbildungen in diesem Manuskript mit PyX erstellt.

Sehen wir uns zunächst an, wie aus einem in einer Datei vorliegenden Datensatz eine graphische Darstellung erzeugt werden kann. Liegt eine Datei foo_pyx.dat mit folgendem Inhalt

1   0
2   1
3   4
4   2.5
5   6

vor, so erzeugt das Programm

1
2
3
4
5

from pyx import *

g = graph.graphxy(width=8)
g.plot(graph.data.file("foo_pyx.dat", x=1, y=2))
g.writePDFfile("foo_pyx")

eine PDF-Datei mit Namen foo_pyx.pdf, die folgendermaßen aussieht.

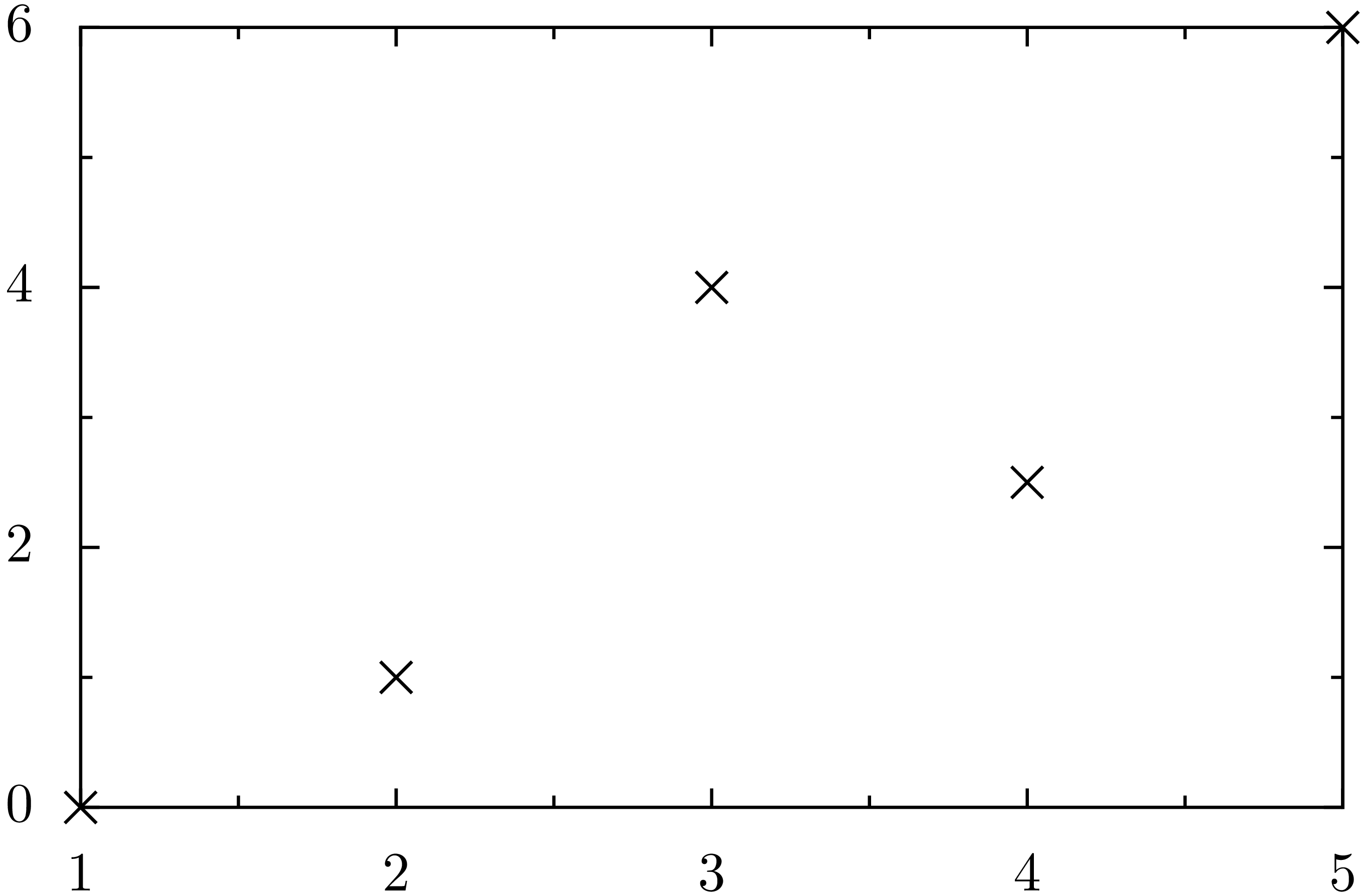
In Zeile 1 wird zunächst PyX importiert. Anschließend wird in Zeile 3 ein zweidimensionaler Graph der Breite 8 erzeugt. Wird die Höhe des Graphen nicht spezifiziert, so ist das Seitenverhältnis durch den goldenen Schnitt gegeben. In Zeile 4 werden die Daten aus der angegebenen Datei eingelesen und in den gerade initialisierten Graphen gezeichnet. Dabei geben die Werte der benannten Argumente x und y die Spalten an, aus denen die jeweiligen Daten zu entnehmen sind. Schließlich wird mit der writePDFfile-Methode die PDF-Datei erzeugt.

Um einen gewissen Einblick in die Möglichkeiten von PyX zu gewinnen, wollen wir diese Graphik nun modifizieren. Dabei erzeugt der Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

from pyx import *

unit.set(xscale=1.3)

g = graph.graphxy(width=8,
                  x=graph.axis.linear(title="$x$"),
                  y=graph.axis.linear(title="$y$")
                 )
g.plot(graph.data.file("foo_pyx.dat", x=1, y=2),
       [graph.style.line([style.linestyle.dashed, color.rgb(0, 0, 1)]),
        graph.style.symbol(graph.style.symbol.circle, size=0.1,
                           symbolattrs=[deco.filled([color.rgb.red]),
                                        deco.stroked([color.grey(0.5)])])])
g.writePDFfile("foo_pyx")

die folgende Grafik

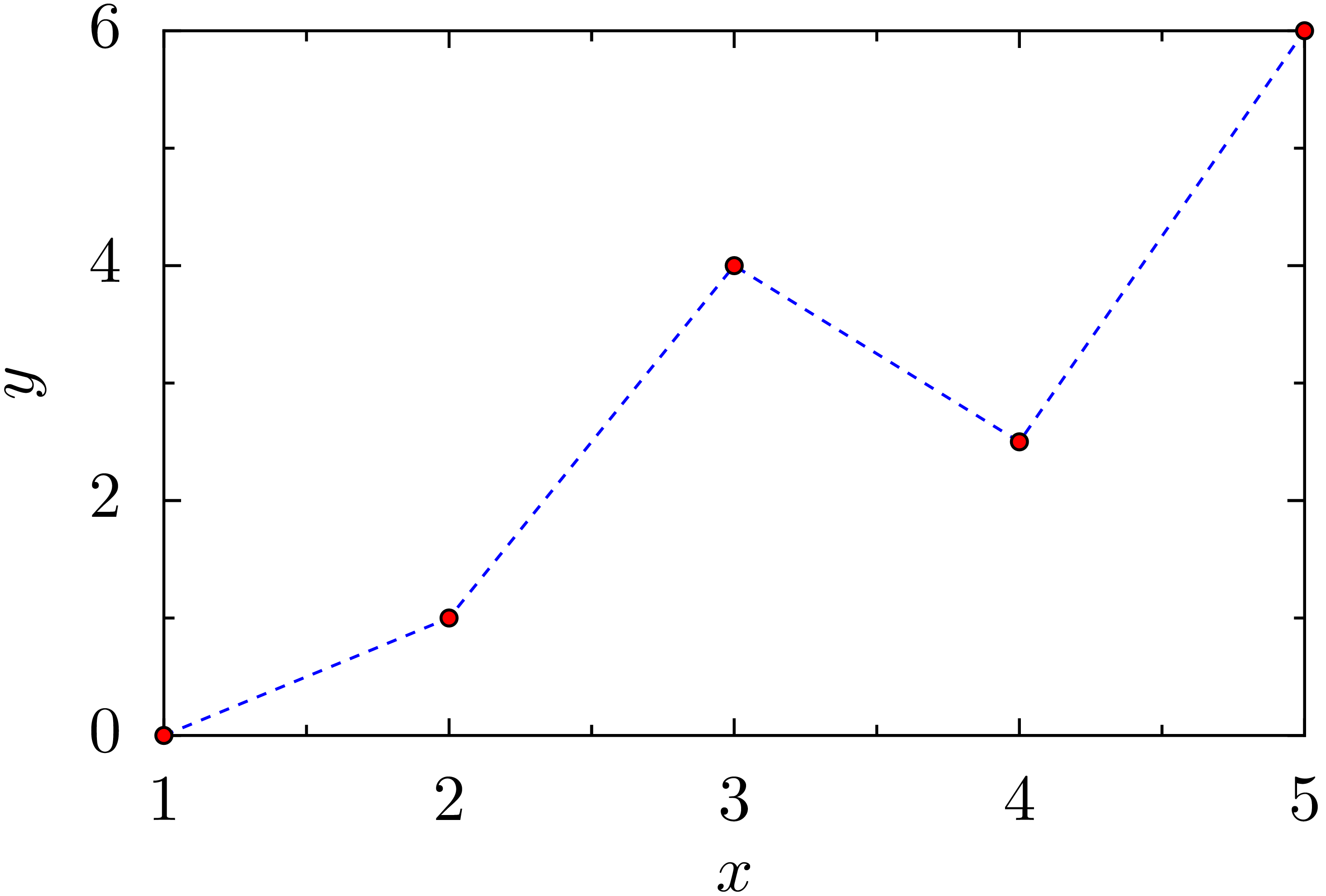
Hier haben wir die folgenden Veränderungen vorgenommen. In Zeile 3 wurden alle Beschriftungen um einen Faktor 1,3 vergrößert. PyX erlaubt es, verschiedene Längen, zum Beispiel Textgrößen und Liniendicken unabhängig voneinander global zu verändern. xscale ist dabei für die Textgröße zuständig. In den Zeilen 6 und 7 wurden die beiden Achsen mit Beschriftungen versehen, wobei die Dollarzeichen durch TeX bedingt sind und ein Umschalten in den Mathematikmodus bewirken. Außerdem werden hier lineare Achsen verwendet. Mit graph.axis.logarithmic könnte man auch logarithmische Achsen verlangen. Zudem wäre es möglich, eigene Achsentypen zu programmieren.

In den Zeilen 9-12 wird die Darstellung der Daten festgelegt. In diesem Fall haben wir angegeben, dass wir die Datenpunkte sowohl durch Symbole darstellen als auch mit Linien verbinden wollen. Letzteres geschieht mit graph.style.line, das als Argument eine Liste von Linieneigenschaften erwartet. Hier haben wir einen gestrichelten Linienstil und die Farbe blau im RGB-Format [6] verlangt. Für die Symbole haben wir mit graph.style.symbol.circle Kreise ausgewählt, deren Größe durch den Wert des Arguments size bestimmt ist. Zudem kann eine Liste von Attributen übergeben werden. Wir verlangen beispielsweise, dass die Kreise rot gefüllt sind, wobei hier zur Abwechslung der Farbenname verwendet wurde. Außerdem wird die Kontur des Kreises in grau ausgeführt, da color.grey mit einem Argument zwischen Null und Eins auf einen Grauwert zwischen schwarz und weiß abgebildet wird. Man sieht in diesem Programmbeispiel, dass man sich einiges an Tipparbeit durch geeignete import-Anweisungen zu Beginn des Programms sparen könnte.

Wir beenden dieses Kapitel mit einem Beispiel von der PyX-Webseite, das die Mächtigkeit des Programmpakets bei Schemazeichnungen demonstriert.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

from pyx import *

p1 = path.curve(0, 0, 1, 0, 1, 1, 2, 1)
p2 = path.circle(1, 0.5, 0.5)

(a1, a2), (b1, b2) = p1.intersect(p2)

x1, y1 = p1.at(a1)
x2, y2 = p1.at(a2)

c = canvas.canvas()
c.fill(path.circle(x1, y1, 0.1), [color.rgb.blue])
c.fill(path.circle(x2, y2, 0.1), [color.rgb.blue])
c.stroke(p1, [color.rgb.red])
c.stroke(p2, [color.rgb.green])
c.writePDFfile("intersect")

Das Ergebnis sieht folgendermaßen aus:

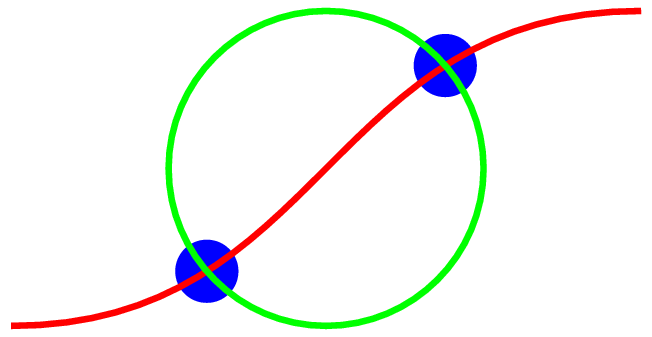
In den Zeilen 3 und 4 werden zunächst zwei Pfade definiert, und zwar eine Bézier-Kurve p1 und ein Kreis p2. In Zeile 6 werden die beiden Pfade miteinander geschnitten. Das Ergebnis sind zwei Tupel, die die Lage der beiden Schnittpunkte entlang der beiden Kurven angeben. Die zugehörigen Koordinaten werden in den Zeilen 8 und 9 mit Hilfe der ersten Kurve bestimmt. In Zeile 11 beginnt das Zeichnen mit der Einrichtung eines »canvas«, also einer Leinwand, auf der gemalt werden kann. Dann werden in den Zeilen 12 und 13 an den zuvor berechneten Schnittpunkten zwei blau gefüllte Kreise mit Radius 0.1 positioniert. Schließlich werden die beiden Pfade in rot bzw. grün gezeichnet und das Ergebnis mit Hilfe der writePDFfile-Methode des Canvas ausgegeben.

Abschließend muss noch einmal betont werden, dass sowohl die Beschreibung von matplotlib als auch die Beschreibung von PyX nur jeweils einen winzigen Ausschnitt aus den Möglichkeiten der beiden Programmpakete darstellen konnten. Einen guten Überblick bieten die oben bereits erwähnten Beispielseiten.